FİNANS FİZİĞİ -16-

Geçmişdeki yazılarımızda, Galilei Denklemi’nin, içinde yaşadığımız evrenin uzay_zamanının sürekli oluşundan, nam-ı diğer, geometrisinden kaynaklandığını yani kısaca, konum değişikliğini zaman cinsinden veren sıradan bir Kuvvet Serisi (‘Power Series’ ve ‘Taylor Series’) olduğundan söz etmiş idik. Böylesi seriler, kuvvet sabit ise, yani konum değişikliğinin zamana göre ikinci dereceden türevi sabit ise, (daha yüksek dereceden türevler otomatikman sıfır olacağından) Galilei Denklemi’ni tıpatıp vermekteydi.
İkinci dereceden türev de yani kuvvet de sıfır ise, Newton Yasaları’nın birincisi, nam-ı diğer Galilei Değişmezlik (‘Invariance’) İlkesi tıpatıp elde edilmekteydi.
Özellkle bu Galilei Değişmezlik (‘Invariance’) İlkesi, Finans Fiziği’nde düz çizgilerden oluşan destek veya direnç düzeyleri olarak belirmektedir. Bu resmin pek çok örneğine yine geçmişteki pek çok yazımızda yer vermiştik.
Şimdi ise, Newton’un Üçüncü Yasası olarak da bilinen Etki=Tepki yasasının Finans Fiziği’ndeki uygulamalarına değineceğiz.
Bu amaçla, günlük kapanış değerlerinden oluşan bir P(n) zaman serisi elde edelim. Burada n harfi, başlangıç olarak seçtiğimiz n=1 gününden sonraki iş günlerini gösteriyor olsun.
Bu durumda, günlük bağıl değişiklikleri B(n) (oransal değişiklikler, logaritmik değişiklikler, ‘log-returns’) şöylece hesaplayabiliriz.

Günlük bağıl değişim değerler G sütununda ve ikinci satırdan itibaren aşağı doğru büyüyen n değerleri için sıralanmış olsun. İlgili Excel komutları şu şekilde olur:
=EĞER(G3>0;G3;0)
ve
=EĞER(G3<0;G3;0) .
Sonra da, mesela, günlük bağıl değişim değerlerinin N gün içinde kaç kez artılı ve eksili olduğu sayılabilir. Hatta daha rafine nice istatistik yöntemler de uygulanabilir.
Hemen alttaki grafikte BIST30 (XU030) endeksine ait 10.04.2002 tarihli kapanışından dünkü 22.03.2025 dahil kapanışı arasındaki veriden oluşturulmuş kırmızı renkli zaman serisi çizgisini ve bundan türetilmiş olan B+(m) ve B-(k) adlı zaman serileri incelenebilir. Fiyat P(n) birimi ₺’dir ama B+(m) ve B-(k) boyutsuz ve birimsizdirler. BIST30 için N=5755 olup B+(m) ve B-(k) adlı zaman serilerinin değer toplamları, sırasıyla ve yaklaşık olarak 41.62 ve -36.44 değerlerine eşittir. Aynı süre içinde BIST30 endeksi 3030 gün bağıl artış ve 2722 gün bağıl azalış sergilemiştir. 3030+2722=5752 olduğuna göre de (5755-5722=) 3 gün bağıl olarak aynı kalmıştır.
Ama, çok daha ilginci, ilgili grafik incelendiğinde görüleceği gibi, artış ve azalışların hemen hemen bakışık (simetrik) oluşudur. Yani, yaklaşık olarak her artışı (azalışı) yaklaşık olarak aynı miktar azalış (artış) izlemiştir. Tam değerlerin arasındaki farklılıklar da endeksin evriliş grafiğini tanımlamıştır.

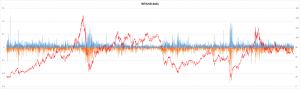
Söz konusu bakışım WTIUSD (ve BRENT) değerlerinde daha belirgindir. Hemen alttaki grafikte WTIUSD zaman serisi 17.10.2001 tarihli kapanışından dünkü 22.03.2025 dahil kapanışı arasındaki veriden oluşturulmuş kırmızı renkli zaman serisi çizgisini ve bundan türetilmiş olan B+(m) ve B-(k) adlı zaman serileri sergilenmiştir. Fiyatların birim (USD) $’dir ve WTIUSD için N=5867 olup B+(m) ve B-(k) adlı zaman serilerinin değer toplamları, sırasıyla ve yaklaşık olarak 52.49 ve -49.48 değerlerine eşittir.

Aynı süre içinde WTIUSD fiyatları 3036 gün bağıl artış ve 2808 gün bağıl azalış sergilemiştir. 3036+2808=5844 olduğuna göre de (5867 -5844=) 23 gün bağıl olarak aynı kalmıştır.

Şu notu düşmeksizin bu yazıyı bitirmek mühim bir eksikliğe yol açardı: Yukarıda anlatılan yaklaşımı kullanarak başka finans araçlarına ve başka zaman periyotları ile ve biraz daha ileri düzey istatiksel analizle destekleyerek ve hele karşılaştırmalı da olursa çok hoş olur, gayet iyi dergilerde basılabilecek makaleler yapabilirsiniz. Söz, ben yapmayacağım. Ama, ihtimaldir ki, o makale(ler ?) hakemliğe bana gelir (!)

Grafiklerin PDF’si için:
Bel1