8.5 Kam Profilinin Elde Edilmesi

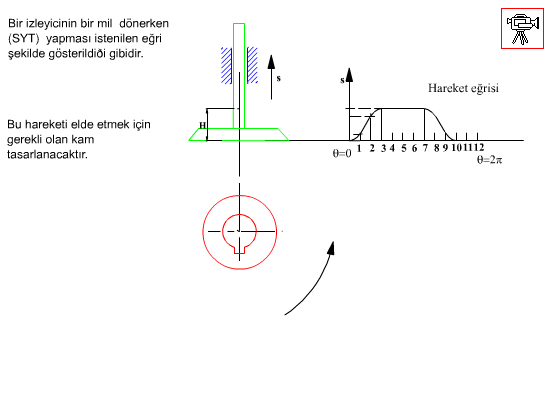
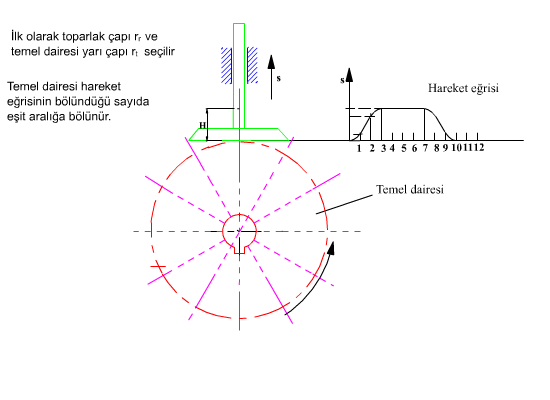
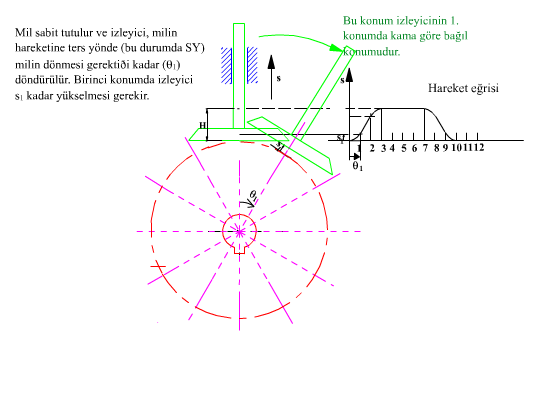
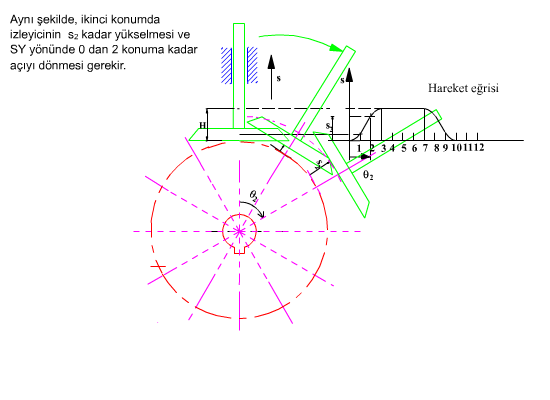
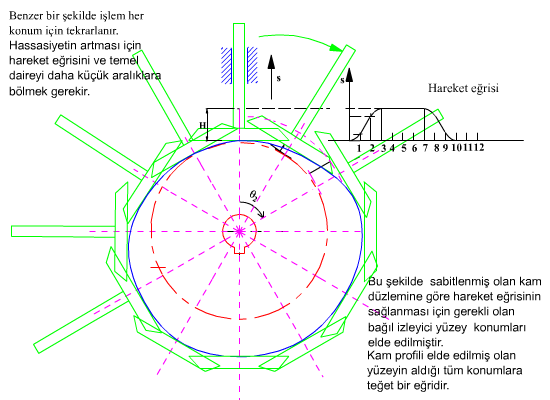
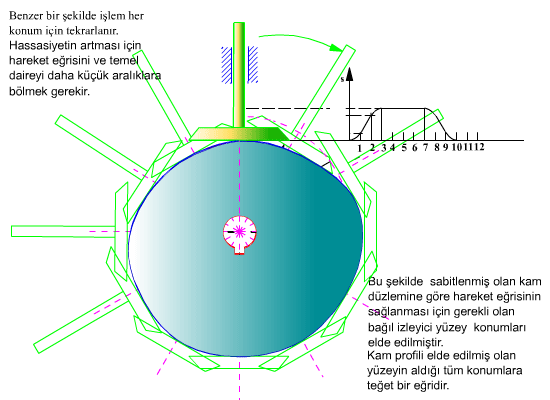
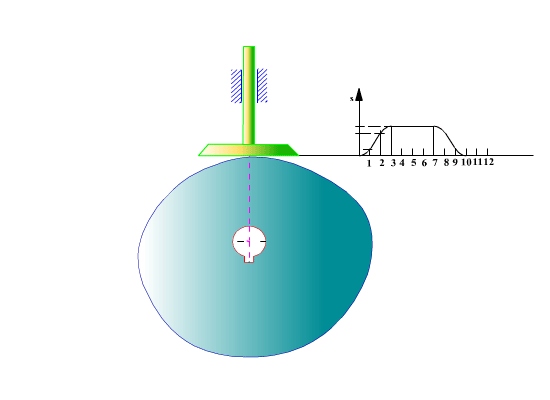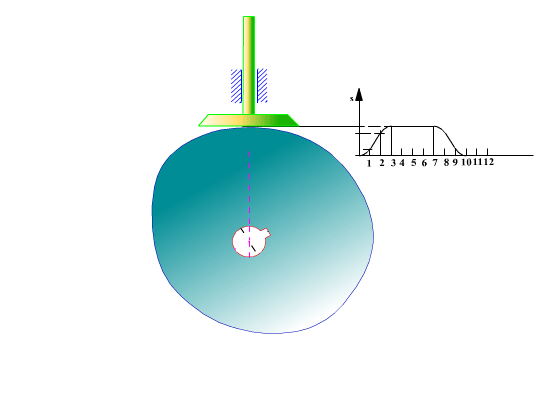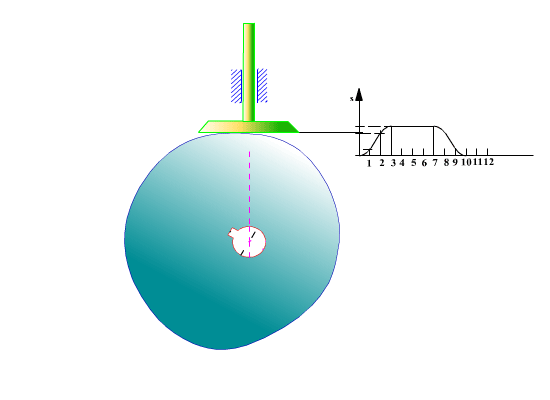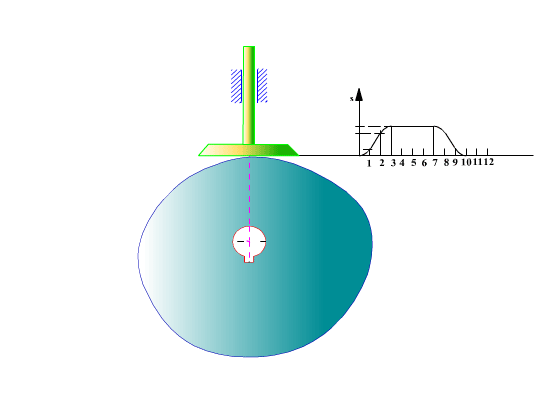
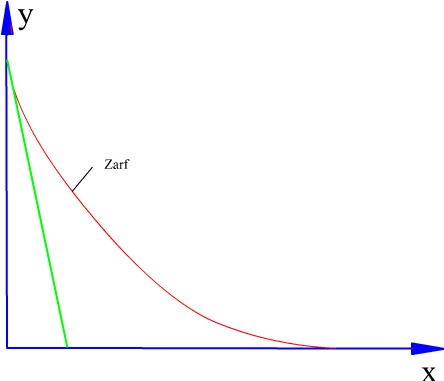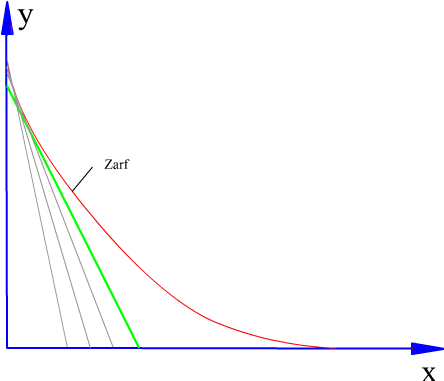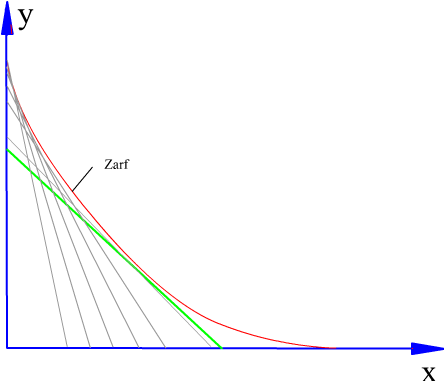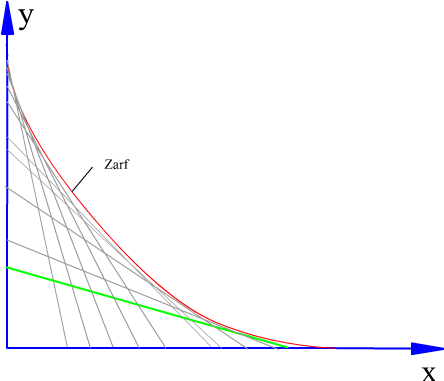
Temel dairesi yarıçapı ve hareket diyagramı belirlendikten sonra kam profilinin elde edilmesi için önceden toparlaklı santrik izleyicili radyal kamda açıklandığı gibi, kinematik yer değişim yapılarak, kam sabit tutulur. Sabit uzuv kama göre dönecek (kamın sabit uzva göre dönme yönünün ters yönünde) ve bu arada izleyici bağıl konumu hareket eğrisine göre belirlenecektir. İzleyicinin her kam açısına göre aldığı konum bir eğri demetini oluşturacaktır. Bu eğri demetinin her bir eğrisine teğet olarak çizilen eğri kam profilidir. Aşağıdaki şekilde ise düz yüzeyli öteleme yapan izleyicili radyal kam profilinin belirli bir hareket eğrisi için elde edilmesi gösterilmektedir.

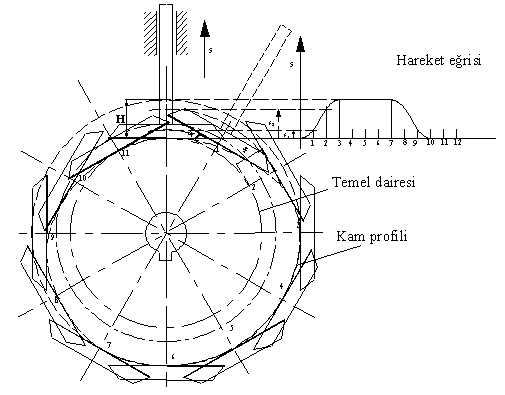
Kam profilini geometrik olarak belirli bir hassasiyette elde edilebilmesi çok sık aralıklarda izleyicinin kama göre bağıl konumunun bulunmasını gerektirir. Bilgisayarda bu geometrik yöntem bir çizim programı kullanılarak uygulansa bile işlem uzun ve yorucudur. Ayrıca günümüzde kam imalatı için numerik kontrollu takım tezgahları kullanıldığından bu tezgahlar için kam profili noktalarını numerik olarak hassas bir şekilde bulmamız lazımdır. Bu nedenlerden dolayı analitik olarak kam profilinin belirlenmesi açıklanacaktır.

Kam profilinin analitik olarak belirlenmesi matematikçiler tarafından geliştirilmiş olan zarf teorisi ile mümkündür. Matematiksel olarak zarf:

Bir eğri demeti içinde bulunan her bir eğri bir başka eğriye teğet ve bu eğrinin her bir noktasında, demeti oluşturan eğrilerden birisi bu eğriye teğet ise, bu eğri bir zarfın tümü veya bir parçasıdır.

Bir parametreli eğri demeti f(x, y, c) = 0 gibi bir denklemle belirlidir. Bu denklemde c değişken parametre olup her c değerinde eğri demetinin bir eğrisi elde edilir. f(x, y, c) fonksiyonunun sürekli olduğunu (istenilen türevlerinin x, y, c parametrelerine göre alınabileceğini ve bu türevlerin sonlu değerler olduğu) varsayılacaktır.

Bu eğri demetinde bulunan bir eğrinin her hangi bir noktasında eğimi:

\displaystyle \frac{{\text{dy}}}{{\text{dx}}}=-\frac{{\partial \text{f/}\partial \text{x}}}{{\partial \text{f/}\partial \text{y}}}

dı. Bu denklemden:

\displaystyle \frac{{\partial \text{f}}}{{\partial \text{x}}}\text{dx}+\frac{{\partial \text{f}}}{{\partial \text{y}}}\text{dy}=0

bağıntısı elde edilir. Bu bağıntı aynı zamanda:

\displaystyle \frac{{\partial \text{f}}}{{\partial \text{x}}}\frac{\text{dx}}{{\text{dc}}}+\frac{{\partial \text{f}}}{{\partial \text{y}}}\frac{\text{dy}}{{\text{dc}}}=0

olarak yazılabilir. Eğim denkleminden elde edilen bu ilişki demetin içinde bulunan her eğri için geçerli olacaktır. Eğer bir başka eğri (zarf) bu eğri demetini oluşturan eğrilere teğet ise, o eğrininde aynı ilişkiyi sağlaması gerekir.

f(x, y, c) = 0 fonksiyonunun toplam türevi:

\displaystyle \frac{{\partial \text{f}}}{{\partial \text{x}}}\text{dx}+\frac{{\partial \text{f}}}{{\partial \text{y}}}\text{dy}+\frac{{\partial \text{f}}}{{\partial \text{c}}}\text{dc}=0

dır, veya:

\displaystyle \frac{{\partial \text{f}}}{{\partial \text{x}}}\frac{\text{dx}}{{\text{dc}}}+\frac{{\partial \text{f}}}{{\partial \text{y}}}\frac{\text{dy}}{{\text{dc}}}+\frac{{\partial \text{f}}}{{\partial \text{c}}}=0

olacaktır. Eğim denkleminden elde edilmiş olan ilişki bu denklemde kullanıldığında:

\displaystyle \frac{{\partial \text{f}}}{{\partial \text{c}}}={{\text{f}}_{\text{c}}}=0

olacaktır. Öğle ise bu eğri demetinin zarfı f(x, y, c) = 0 denklemini sağlaması gerektiği gibi f_c = 0 kısmi türevini de sağlamalıdır. Bu iki denklemden c parametresinin yok edilmesi ile elde edilen g(x, y) = 0 eğrisi eğri demetinin zarfıdır.

Bazi durumlarda bir eğri demeti parametrik denklem şeklinde gösterilebilir. Yani, eğri demeti:

x = ϕ(s, c)

y = ψ(s, c)

şeklinde verilebilir. Burada s eğri parametresi, c ise demet parametresidir. Zarf bu denklemlerden ve:

\displaystyle \frac{{\partial \text{ϕ}}}{{\partial \text{s}}}\frac{{\partial \text{ψ}}}{{\partial \text{c}}}-\frac{{\partial \text{ϕ}}}{{\partial \text{c}}}\frac{{\partial \text{ψ}}}{{\partial \text{s}}}=0

denkleminden c parametresinin yok edilmesi ile elde edilir.

Örnek 4:

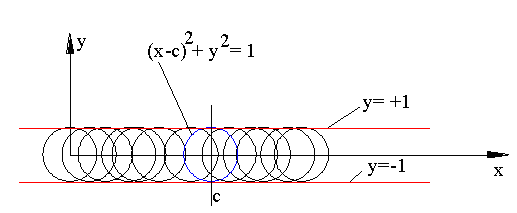
f(x, y, c) = (x − c)² + y² − 1 = 0

denklemi ile verilen eğri demetinin zarfını bulalım. Şekilde gösterildiği gibi, eğri demeti merkezi x = c ve y = 0 ve yarıçapı bir birim olan dairelerdir. Her c değeri için demetin bir eğrisi elde edilir. Denklemin c parametresine göre türevi:

f_c = −2(x − c) = 0

f ve f_c denklemlerinden c parametresi yok edildiğinde:

y = ±1

elde edilir. Bu zarf eğrisi, şekilde görüldüğü gibi daire demetine teğet, yatay doğrulardır.

Örnek 5:

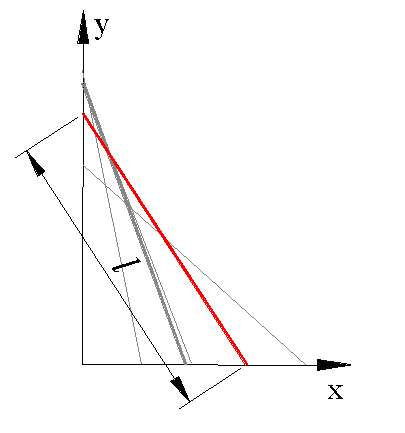
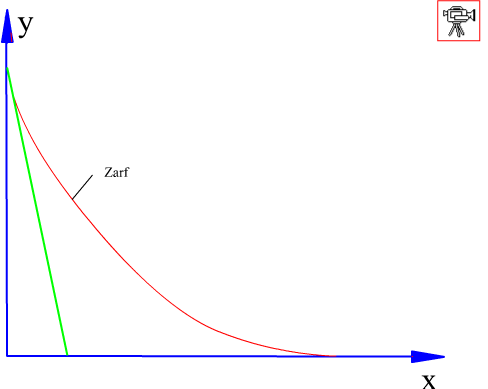
Bir ucu duvara dayalı, bir ucu yerde duran bir merdivenin sürtünmenin az olmasından dolayı düşerken yaptığı hareketi ele alalım. Merdivenin farklı konumları bir eğri demetini oluşturacaktır. Bu sırada oluşturulan zarfı bulalım:

Parametrik olarak merdivenin denklemi:

y = −x tanγ + l sinγ

dir. γ merdiven ile yatay arasinda kalan açi, l ise merdiven uzunluğudur. Bu denklemi:

f(x, y, γ) = y + x tanγ − l sinγ = 0

şeklinde yazabiliriz. Denklemin γ ya göre kısmi türevi ise:

f_γ(x, y, γ) = x/cos²γ − l cosγ = 0

olacaktır. Bu iki denklemden x ve y için çözüm yapıldığında:

x = l cos³γ

y = l sin³γ

dir. Bu iki denklem zarf eğrisini parametrik olarak tanimlamaktadir ve zarf bu denklemlerle çizilebilir. Eğer γ parametresini bu iki denklemden yok edersek:

x^2/3 + y^2/3 = l^2/3

denklemi elde edilir (bu astroid eğrisidir).

Örnek 6:

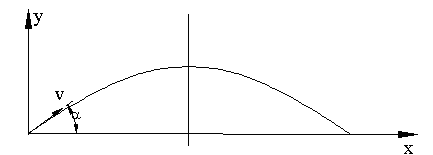
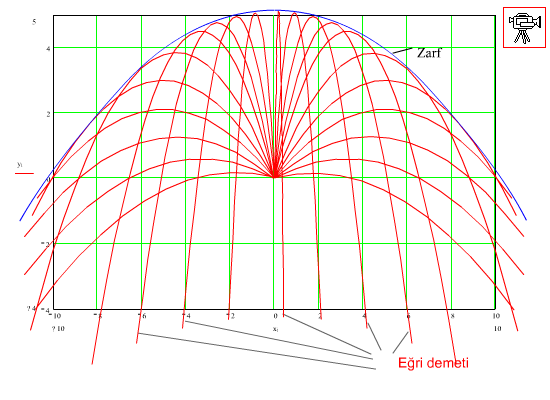
Bir top kullanılarak ilk hızı v olan mermiyi yatay ile α açısı yapacak şekilde atıyoruz. Bu merminin etkisi altında olabilecek alan (vurabileceğimiz hedefler) neresidir.

Problem klasik eğik atış problemidir. Mermi x yönünde sabit hız, y yönünde ise sabit yer çekimi ivmesi ile hareket edeceğinden eğri demeti parametrik olarak:

x = v cos(αt)

y = v sin(αt) − ½gt²

dir. Denklemlerden t parametresi yok edildiğinde:

f(x, y, α) = ½x² − [(v²/g)sinαcosα]x + [(v²/g)cos²α]y = 0

parabol eğrisi elde edilir. Denklemin α parametresine göre türevi:

f_α(x, y, α) = −(v²/g)[x(cos²α − sin²α) + 2ysinαcosα] = 0

dır. Bu denklem basitleştirildiğinde:

cos(2α) x + sin(2α) y = 0

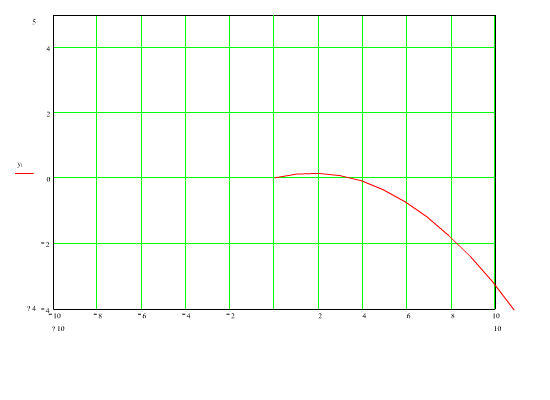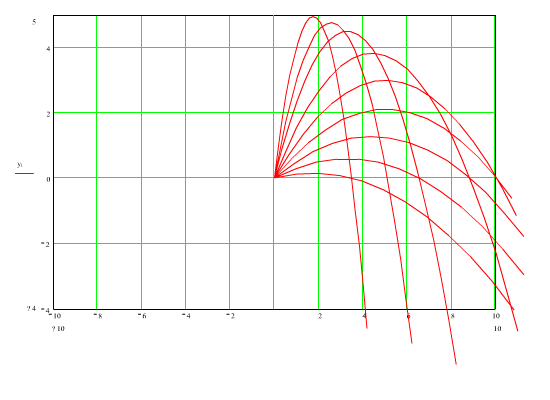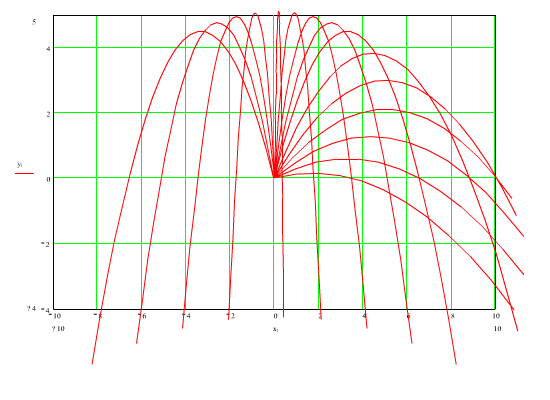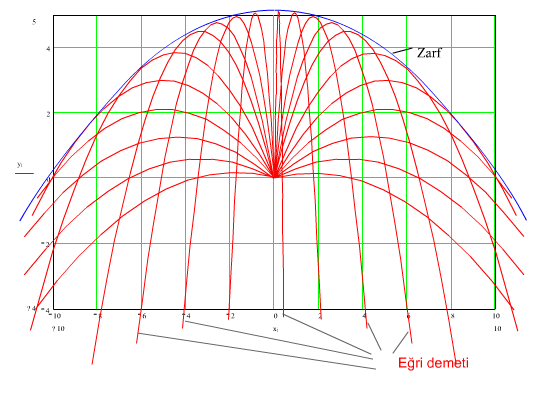
şeklinde yazılabilir. f(x, y, α) ve f_α(x, y, α) denklemlerinden α yok edildiğinde zarf eğrisi:

y = ½[v²/g − gx²/v²]

şeklinde bulunur. Bu denklem bir paraboldür. Sonuç asağıda gösterilmektedir. Bu zarf eğrisinin (parabolün) altında kalan noktalara atış yapılabilir.

Yukarıda anlatılmış olan zarf teorisinin kam mekanizmalarına uygulamaları olarak:

A-) Toparlaklı, öteleme yapan izleyicili radyal kam profili için burayı tıklayın.
B-) Düz yüzeyli öteleme yapan izleyicili radyal kam profili için burayı tıklayın.
C-) Toparlaklı salınım yapan izleyicili kam profili için burayı tıklayın.
D-) Şekil kapalı kam profili için burayı tıklayın.