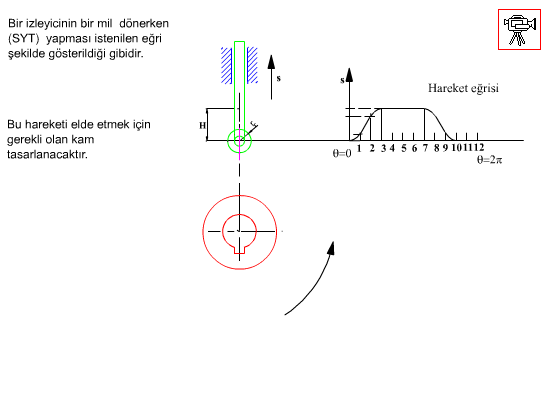
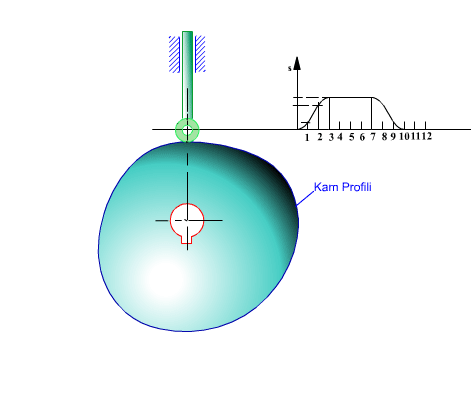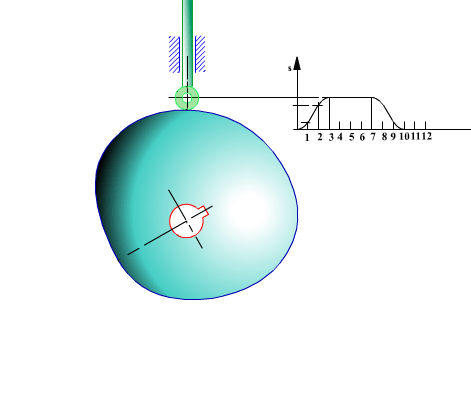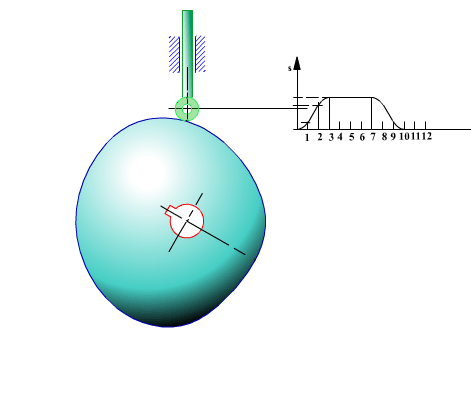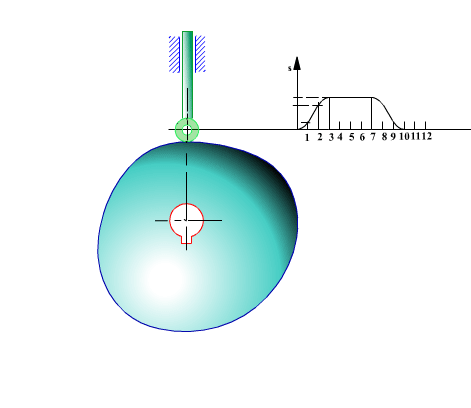
Toparlaklı, öteleme yapan izleyicili radyal kam profilinin elde edilmesi:
Hareket eğrisi s(θ) ve türevleri kamın tam bir devri için bilinmektedir. Şekilde gösterildiği gibi, izleyici öteleme ekseni kam merkezinden, c kadar kaçıktır (c = 0 oldugunda santrik öteleme yapan izleyici olacaktır).

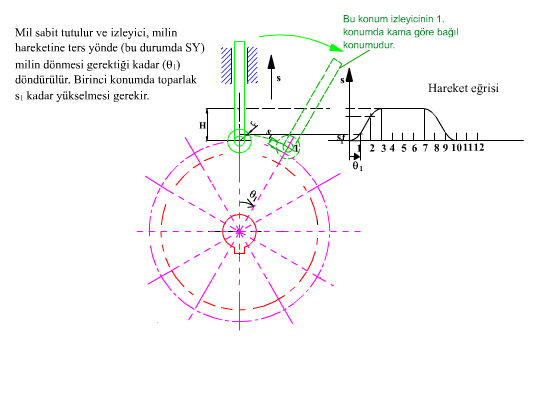
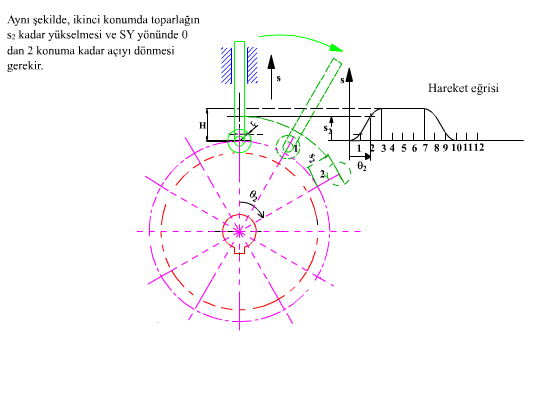
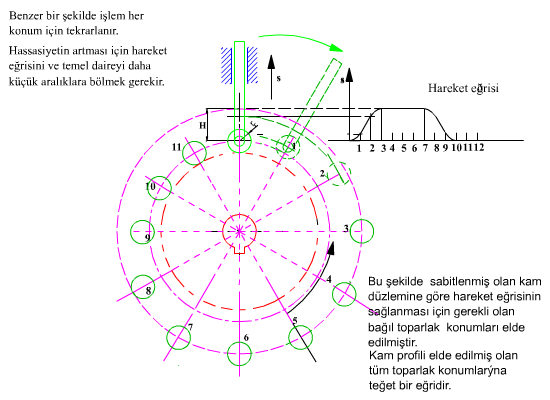
Her hangi bir θ açısı ve buna karşı gelen s yükselme uzunluğunda toparlağın kama göre bağıl konumu yukarıda görülmektedir.
Yukarıda kam profilinin geometrik olarak elde edilmesi (eksantrikliğin olmadığı durum için) açıklanmıştır. Şimdi zarf teorisini öteleme yapan toparlaklı radyal kam için uygulayalım ve bu yöntemle kam profilini daha hassas bir şekilde analitik olarak elde edelim.
Toparlak dairesinin farklı konumlari eğri demetini oluşturmaktadır ve bu eğri demetinin denklemi:
(x − xp)2 + (y − yp)2 − rr = 0 (1)
dır. Bu denklemde rr toparlak yarıçapı ve P(xp, yp) toparlağın merkez koordinatlarıdır. xp ve yp kam dönme açısının bir fonksiyonudur ve:
xp = c cosθ + (k + s) sinθ
yp = −c sinθ + (k + s) cosθ (2)
dır. Burada
k = \displaystyle \sqrt{{{{{\left( {{{\text{r}}_{\text{t}}}+{{\text{r}}_{\text{r}}}} \right)}}^{2}}-{{\text{c}}^{2}}}}
dir. Kam daire merkezi istenir ise karmaşık sayılar kullanılarak yazılabilir. Bu durumda
z = xp + iyp = ce−iθ + i(k + s)e−iθ
olacaktır ki reel ve sanal kısımları toparlak dairesinin x ve y koordinatlarını verir.
Dikkat edilir ise toparlak dairesinin olusturduğu eğri demeti fonksiyonu sabit rt, rr, c parametreleri dışında s ve θ ya bağlıdır. s yükselme mesafesinin de hareket diyagramından θ nın bir fonksiyonu olduğu düşünülür ise, eğri demeti fonksiyonu f(x, y, θ) şeklinde olup her θ açısına göre belirli bir merkezi ve rr yarıçapı olan bir daire denklemi elde edilecektir. Şimdi:
f(x, y, θ) = (x − xp)2 + (y − yp)2 − rr = 0 (1)
denkleminin θ parametresine göre kısmı türevi alınır ise:
fθ(x, y, θ) = −2(x − xp)∂xp/∂θ − 2(y − yp)∂yp/∂θ = 0 (3)
olacaktır. Bu denklemde:
∂xp/∂θ = (∂s/∂θ − c)sinθ + (k + s)cosθ
∂yp/∂θ = (∂s/∂θ − c)cosθ − (k + s)sinθ (4)
dır. (1) ve (3) denklemlerinden θ parametresinin yok edilmesi genelde s hareket diyagramından dolayı mümkün değildir (dıyagram karmaşık birkaç denklemden oluşmaktadır). Bu nedenle eğri demetinin zarfı olan kam profil eğrisi çok basit problemler haricinde parametrik olarak elde edilir. 1 ve 3 denklemlerinden kam profili koordinatlari (x, y) her θ açısı için:
x = xp ± \displaystyle \frac{{{{\text{r}}_{\text{r}}}}}{{\sqrt{{1+{{{\left( {\frac{{\partial {{\text{x}}_{\text{p}}}\text{/}\partial \text{θ}}}{{\partial {{\text{y}}_{\text{p}}}\text{/}\partial \text{θ}}}} \right)}}^{2}}}}}}
y = yp − (x − xp) \displaystyle {\frac{{\partial {{\text{x}}_{\text{p}}}\text{/}\partial \text{q}}}{{\partial {{\text{y}}_{\text{p}}}\text{/}\partial \text{q}}}} (5)
xp, yp ve θ ya göre türevleri denklem 2 ve 4 de verildiği gibidir. Dikkat edilir ise, her θ değeri için iki nokta elde edileceğinden kam eğri demetinin zarfı olan kam profili iki kısımdan oluşacaktır. Bunlardan birisi dıştan temas eden kam profilini digeri ise içten temas eden bir kam profilini verir.
Örnek 7:
120° kam dönme açısında 50 mm basit harmonik hareket ile yükselen, 60° bekleme yapan, 120° kam dönme hareketi ile geri dönen, toparlak yarıçapı 20, temel daire yarıçapı 50 mm ve 20 mm eksantrikliği olan kam sisteminde kam profilini bulalım.
Bu örnek MathCad paket programı kullanılarak çözülmüştür.
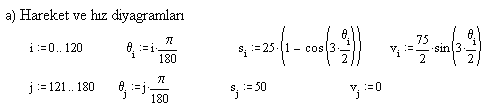
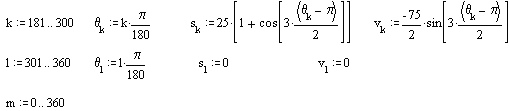
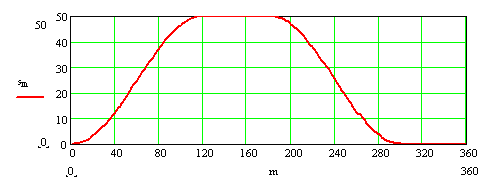
Hareket diyagramı (dikkat edilir ise, dört ayrı eğriden oluşmaktadır)
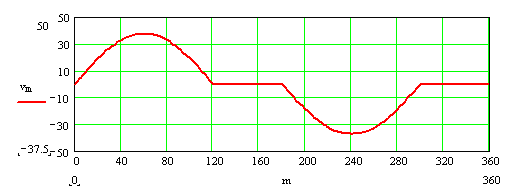
Hız diyagramı (ω = 1 rad/s olduğundan v = ds/dθ dır)


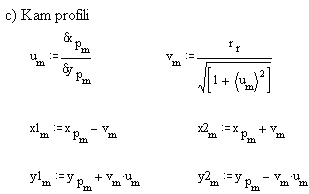
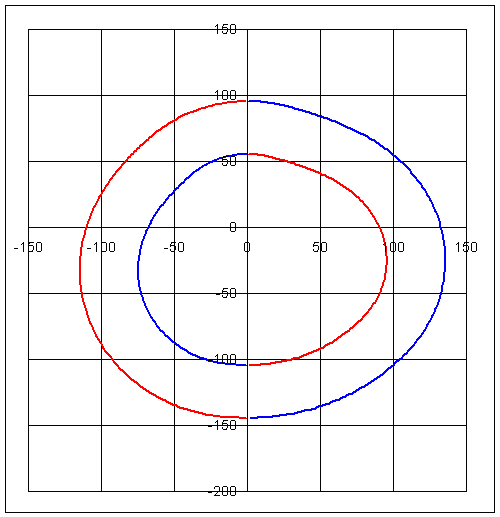
Dikkat edilir ise, denklemde bulunan + ve – değerlere göre her θ açısına göre iki kam eğrisi koordinatı elde edilmektedir. x1, y1 ve x2, y2 koordinatları belirli bir aralıkta dış eğriyi, belirli bir aralıkta ise iç eğriyi belirler.
Sadece dıştan temas eden kamın çizilmesi için ise, bu koordinatlardan merkeze daha yakın olan koordinat seçilmelidir. Bunun için her θ açısına karşı gelen iki koordinatın merkezden uzaklığı bulunarak birbiri ile karşılaştırılır, merkeze daha yakın koordinat aradığımız kam eğrisi koordinatıdır:


Dikkat edilir ise kam profili kartezyen koordinatlara göre (x, y) polar koordinatlara göre ise (ρ, ξ) olarak elde edilmiştir. Polar koordinatlar kullanılarak çizim şekilde görülmektedir:
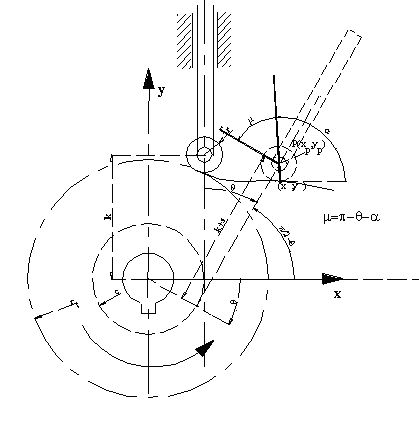
Bu kam mekanizmasında bağlama açısının bir devirde değişimini belirlemek için yukarıdaki şekilden yararlanarak her bir konumda bağlama açısını bulabiliriz.
Mathcad kullanılarak bu açı hesaplandığında:
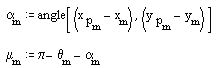
Bağlama açısının 0° < μ < 90° olması için:
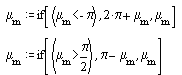
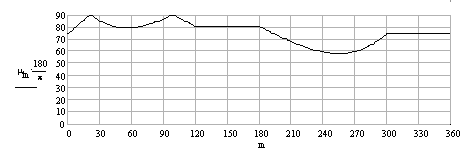
Bağlama açısının bir devirde değişimi şekilde gösterilmiştir. Görüldüğü gibi, yükseliş sırasında μmin = 75°, geri dönüş sırasında ise μmin = 58.23° olmaktadır.

Bu kam yüzeyini rk yarıçaplı bir kesici ile numerik kontrollu bir freze tezgahında işleyeceğimizi düşünelim. Gösterilen konumda kesicinin kam profilinde (x, y) koordinatlarını sağlaması için freze mili O′ merkez koordinatları (xk, yk), bilinen toparlak merkezi ve kam profil eğrisine göre:
xk = x + rk cosψ
yk = y + rk sinψ
olacaktır. Bu denklemde:
ψ = tan-1[(yp − y)/(xp − x)]
dır. Örneğimizde, kam profilini 60 mm çaplı bir kesici ile işleyeceğimiz var sayılır ise, MathCad kullanılarak kesici eksen koordinatları:

Polar koordinatlara göre:
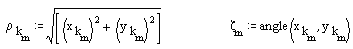
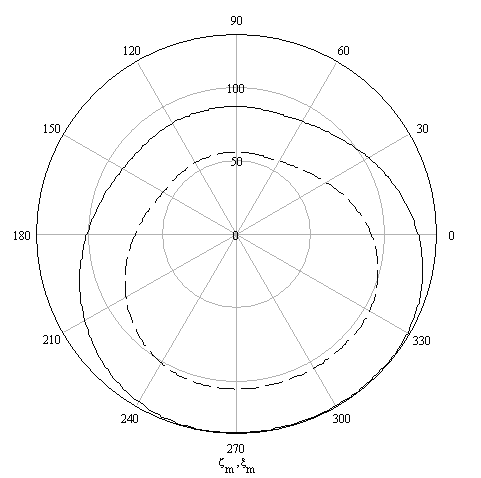
Elde edilen kesici eksen yörüngesi, kam eğrisi ile birlikte (kesik çizgi) şekilde gösterilmiştir. Dikkat edilir ise, bu yörünge kam eğrisine paralel bir eğri değildir (bekleme konumları hariç).