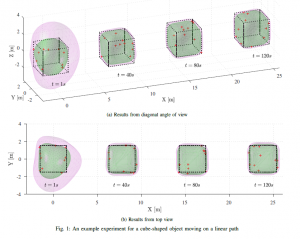
In this study, we consider the challenging task of tracking dynamic 3D objects with unknown shapes by using sparse point cloud measurements gathered from the surface of the objects. We propose a Gaussian process based algorithm that is capable of tracking the dynamic behavior of the object and learn its shape in 3D simultaneously. Our solution does not require any parametric model assumption for the unknown shape. The shape of the objects is learned online via a Gaussian process. The proposed method can jointly estimate the position, orientation, and the shape of the object. The inference is performed by an extended Kalman filter which is suitable for online real-time applications. Lastly, we demonstrate the initial results of a promising approach, which aims at reducing the computational complexity.

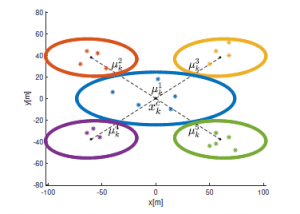
In this paper, we consider the problem of extended target tracking, where the target extent cannot be represented by a single ellipse accurately. We model the target extent with multiple ellipses and solve the resulting inference problem, which involves data association between the measurements and subobjects. We cast the inference problem into sequential Monte Carlo (SMC) framework and propose a simplified approach for the solution. Furthermore, we make use of the Rao-Blackwellization, aka marginalization, idea and derive an efficient filter to approximate the joint posterior density of the target kinematic states and target extent. Conditional analytical expressions, which are essential for Rao-Blackwellization, are not available in our problem. We use variational Bayes technique to approximate the conditional densities and enable Rao-Blackwellization.

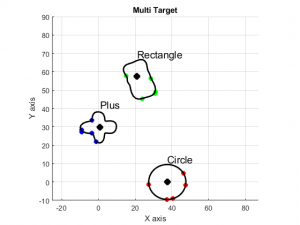
Recent extended target tracking algorithms provide reliable shape estimates while tracking objects. The estimated extent of the objects can also be used for online classification. In this work, we propose to use a Bayesian classifier to identify different objects based on their contour estimates during tracking. The proposed method uses the uncertainty information provided by the estimation covariance of the tracker.

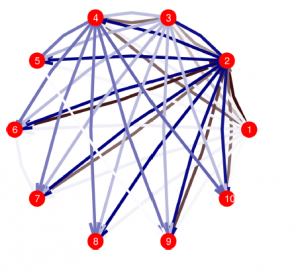
This paper presents a method for inferring interaction strength and structure amongst targets in multiple target tracking (MTT) applications. By making simple assumptions, it is shown how an efficient and well-mixing MCMC inference method can be developed to learn about the relationships between tracked targets, including leader-follower relationships, group relationships and the influence of targets on others. This network structure of influence between targets is inferred in a sparse way, setting many interaction terms to zero and allowing for more efficient inference and clearer structural conclusions to be drawn. The effectiveness of the method is demonstrated on both synthetic and real animal flocking data.

In this work, we present an online method for joint state and parameter estimation in jump Markov non-linear systems (JMNLS). State inference is enabled via the use of particle filters which makes the method applicable to a wide range of non-linear models. To exploit the inherent structure of JMNLS, we design a Rao-Blackwellized particle filter (RBPF) where the discrete mode is marginalized out analytically. This results in an efficient implementation of the algorithm and reduces the estimation error variance.

In this work, we propose using Gaussian processes to track an extended object or group of objects, that generates multiple measurements at each scan. The shape and the kinematics of the object are simultaneously estimated, and the shape is learned online via a Gaussian process. The proposed algorithm is capable of tracking different objects with different shapes within the same surveillance region. The shape of the object is expressed analytically, with well-defined confidence intervals.

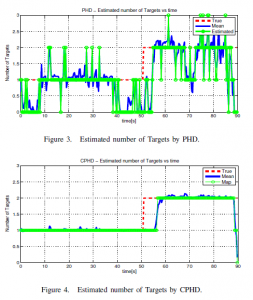
In this work, we explore the potential of networked microphone arrays for multiple target tracking. Tracking is accomplished by using the direction-of-arrival (DOA) estimates of multiple microphone arrays. Each microphone array obtains the DOA estimates by using the wideband extensions of the multiple signal classification (MUSIC) technique. Based on these DOA estimates, multi-target tracking is done by using Probability hypothesis density (PHD) and cardinalized probability hypothesis density (CPHD) algorithms.

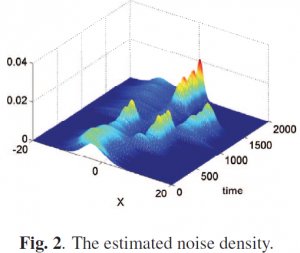
In this study, we investigate online Bayesian estimation of the measurement noise density of a given state space model using particle filters and Dirichlet process mixtures. Dirichlet processes are widely used in statistics for nonparametric density estimation. In the proposed method, the unknown noise is modeled as a Gaussian mixture with unknown number of components. The joint estimation of the state and the noise density is done via particle filters. Furthermore, the number of components and the noise statistics are allowed to vary in time. An extension of the method for the estimation of time varying noise characteristics is also introduced.

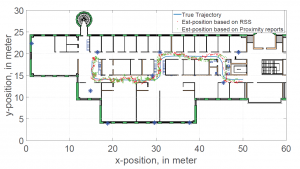
The commercial interest in proximity services is increasing. Application examples include location-based information and advertisements, logistics, social networking, file sharing, etc. In this paper, we consider positioning of devices based on time series proximity reports from a mobile device to a network node. This corresponds to nonlinear measurements with respect to the device position in relation to the network nodes. Therefore, particle filtering is applicable for positioning. Positioning performance is evaluated in a typical office area with Bluetooth-low-energy beacons deployed for proximity detection and report. Accuracy is concluded to vary spatially over the office floor, and in relation to the beacon deployment density.