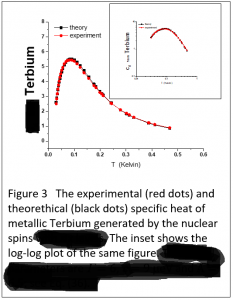
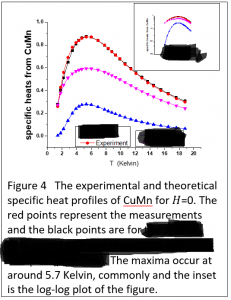
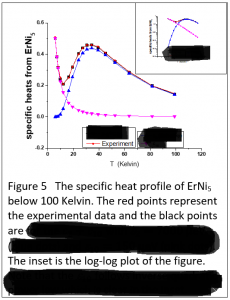
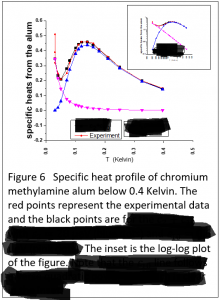
Fizik –12–
İçerik: Her şeyde her şey var mı?
Ön not: Bu yazıda ∞ simgesi, ‘bilinen Gerçek Sayıların en büyüğü’ anlamında kullanılacaktır.
Bakınız; 3’ün karesi 9, 4’ün karesi 16, 16’ya 9’u ekle 25 ve 25 de 5’in karesi. Demek ki,
Eşitlik 1: 3²+4²=5².
Aynı şekilde; 6’nın karesi 36, 8’in karesi 64, 64’e 36’yı ekle 100 ve 100 de 10’un karesi. Demek ki, Eşitlik 2: 6²+8²=10².
Bu son eşitliğin her iki tarafında 4’ün katı olan Doğal Sayılar var.
4(3²+4²)=4(5²).
Son eşitliğin her iki tarafını 4’e bölersek
3²+4²=5²
elde edilir.
Buradan da şöyle bir öneri çıkarsanabilir: A²+B²=C² ise N herhangi bir sıfırdan farklı Doğal Sayı olmak koşuluyla
(NA)²+(NB)²=(NC)²
olduğu, kolay bir Tümevarım Yöntemi uygulamasıyla gösterilebilir. (*)
Demek ki, A²+B²=C² eşitliğini sağlayan ∞ kadar A, B ve C gibi Doğal Sayı üçlüğü mevcuttur. Bu tür sayılara Pisagor Üçlü(k)leri denir. (**)
Şuna da dikkat etmeli;
3²+4²=4²+3²=5² yani 4²+3²=5².
Son eşitliğin iki tarafını da 4 ile çarparsak eşitlik bozulmaz;
(2×4)²+(2×3)²=(2×5)² yani
8²+6²=10²
elde edilir. Ama şu da bir Pisagor Üçlüğü’dür;
8²+15²=17²
ve buradan da yeni bir ∞ kadar Pisagor Üçlüğü elde edilebilir.
Dahası, herhangi bir Pisagor Üçlüğü herhangi bir (pozitif veya negatif) Gerçek Sayı ile çarpıldığında da yeni Pisagor Üçlükler elde edilir.
Pisagor’dan önceki binlerce yıldır bilinen bu gerçeklerin üçgen şekiller ile ilgisini ilk fark eden(lerden biri ?) Pisagor idi yazılı belgelere göre.
Dik Açı’lı Üçgenler (Dik Üçgenler) bağlamında, herhangi bir Pisagor Üçlüğü’nü her hangi bir parametre ile çarpmak, ilgili üçgenin kenar uzunluklarını aynı parametre ile çarpmak, yani o üçgeni küçültmek ya da büyültmek anlamına gelmekteydi. Bu sırada, açıların aynı kaldığını akılda tutmalı.
Dahası, en küçük Tam Sayı’sı tek, çift veya asal olan Pisagor Üçlükleri ile Dik Üçgenler arasında Bire-Bir Gönderim (‘One to One Mapping’) ilişkisi yoktur. Bu ilişki Örten Gönderim (‘Onto Mapping’) olarak nitelenebilir.
Öte yandan şu soru da hayli ilgi çekicidir: A, B ve C’nin Gerçek Sayı olması halinde de yukarıdaki eşitlikler sağlanır mı acaba? Gayet tabii! Lâkin bir şartla; karekök almayı biliyor olmak yetmez. Karekök alarak bulunacak sonucun da sonlu bir Gerçek Sayı olması gerekir. Her Gerçek Sayı çiftini birbirine bölerek çeşitli sonlu veya sonsuz Gerçek Sayılar elde etmek mümkündür. Örneğin 1’i 3’e bölerseniz 0,333… elde edersiniz. 0,333… sonlu bir sayı değil, sonu olmayan yani sonsuz bir sayıdır. Başka örnek şudur; 0,999… sonsuz bir sayıdır ama 1 sonlu bir sayıdır. Ayrıca, Eşitlik 1 ve 2 sayesinde tanımlanan Pisagor Üçlükleri dizisi de sonsuzdur; yani, orada son üçlünün ne olduğu bilinemez, saptanamaz.
Evet, tarihsel belgelere göre ilk kez şu bizim pek sevdiğimiz Zeno’nun kullandığı anlamdaki sonsuz kavramını tam olarak karşılayabilecek kapasiteye sahip bir sözcük ne güzel Türkçe’mizde var, ne İngilizce’de, ne Latince’de, ne de hatta Grekçe’de. (***)
Latince’deki ‘finitum’ sözcüğü güzel Türkçe’mizde ‘bitmiş’ anlamına gelmektedir (****), İngilizce’deki ‘finite’ sözcüğü de bitimli, sonlu, sınırlı anlamına gelmektedir. Latince’deki ‘infinitum’ sözcüğünün Grekçe karşılığı ise ‘άπειρο’ (‘άperio’) olup sonsuz, yani sonu olmayan anlamındadır. İngilizce’deki ‘endless’ sözcüğü de sonsuz anlamındadır. Demek ki, 1/3, 2/3, 2’nin karekökü, altmış derecenin sinüsü gibi sayılar sonsuzdur ve bir, üç buçuk ve virgülden sonra basamağı olmayan Tam Sayılar ile virgülden sonraki basamak sayısı sınırlı olan Gerçek Sayılar sonlu sayılardır.
Açıktır ki, Dik Üçgen Geometri’sinde kenar uzunluklarının Tam Sayı mı, Gerçek Sayı mı, sonlu sayı mı, sonsuz sayı mı olduğu ile hemen hiç ilgilenilmez. Demek ki, birbirinden farklı Dik Üçgenlerin sayısı birbirinden farklı Pisagor Üçlükleri’nin sayısından fazladır.
Pisagor da, ihtimalen bütün bu gerçekleri bilmekteydi. Hatta, yine ihtimaldir ki, Pisagor’dan başkaları da Dik Üçgen kenar uzunlukları arasındaki ilişkiyi (Pisagor’dan bağımsız olarak) bulgulamıştı. Ama, sadece Pisagor’a ilişkin yazılı belge varlığı nedeniyle ilgili buluş bilgisi onun adıyla kaydedilmiştir.
Gelgelelim, aynı kayıtlara göre, Pisagor’un Fizik ile ilgisi genellikle göz ardı edilir. Pisagor, telli çalgılarda sesin oluşumu ile yakından ilgilenmiştir ve bir telden yayılan sesin harmonik olduğunu yani aynı anda ∞ kadar farklı dalga boyuna sahip ses çıktığını bulgulamıştır. Dahası, bunlardan en bas olanının yarı dalga boyu, tel uzunluğu kadar olmalı; daha tiz (ince) olanların dalga boyu da bu en bas (kalın), temel sesin bir buçukda biri, ikide biri (yarısı), iki buçukda biri, … olmalıdır. Çünkü, teldeki titreşimlerin boğum (‘node’) denen kımıltısızlığa denk gelen bölümler telin iki ucunda oluşmalıdır. (#) Bu nedenle de iki telden uzun olanı kalın sesleri yoğunlukla, kısa olanı da ilkine kıyasla ince sesleri daha yoğun olarak yayar.
Pisagor’dan yaklaşık 2000 yıl sonra, G. Galilei’nin babası Vincenzo Galilei müzikçiydi, lavta çalardı. (##) Bundan sebep olacak, tellerden çıkan seslerle çok yakından ilgilenmiş ve telden çıkan seslerin tel boyu ile ilintili olduğunun yanı sıra teldeki gerilimle de değiştiğini bulgulamıştı. Çalgıcıların, örneğin kemancıların ve gitarcıların bir takım düğmeleri çevirerek onlara bağlı telleri gererek ya da gevşeterek tellerden doğru seslerin, örneğin la telinden la sesinin çıkmasını sağladıkları yani aletlerini acort ettikleri (‘tuning’) anımsanmalıdır.
Bakınız, şimdi de, yükseklik değeri ∞ olan bir Potansiyel Kuyusu içinde hapsolmuş bir nokta parçacığın kuvantum fiziğini irdeleyelim (####) ve aynı anda Pisagor’u sessizce analım.
İlkin, bu kuyu tek boyutlu ve L genişliğine sahip olsun. Demek ki, taneciğimiz bu L genişliğindeki kuyunun dışına çıkamaz. Yani, demek ki, taneciğimizin De Broglie dalgasının dalga boyu (λ) ancak 2L, L, 2L/3, … ve özetle N sıfırdan farklı bir Tam Sayı ise, λ=2L/N olabilecektir. Yani, basamaklı (‘quantized’) değerlere sahip olabilecektir.
İkincileyin, Einstein-De Broglie eşitliği olan pλ=h eşitliğini doğrusal momentum (p) yani kütle (m) ve sürat (v) niceliklerinin çarpımı (p=mv) olarak değerlendirdiğimizde (mv)(2L/N)=h eşitliğini elde edebiliriz. Buradan v’yi eşitlik solunda bırakarak diğer terimleri eşitlik sağına alırsak
v=Nh/(2mL)
eşitliğini elde ederiz. Bu da bizi E enerji değerleri için
E=mv²/2=N²(h²/8mL²) ifadesine götürür.
Son eşitlikte görüldüğü gibi, dalga boyunun basamaklı oluşu nedeniyle enerji de basamaklıdır.
Kuyu içindeki parçacık v hızıyla devinir ama L genişliğinin dışına çıkamaz görüşü şöyle yorumlanabilir (‘interpretation’): Potansiyel duvarlarının değeri ∞ kadar olduğu için buraya çarpan parçacığın kinetik enerjisinde kayıp olmaksızın, yani Tam Elastik Çarpışma yaparak geri döner. Hızın yönü değişir ama büyüklüğü yani sürat değişmez.
‘Potansiyel duvarlarının yükseklik değeri ∞ kadar değil de sınırlı olsaydı, parçacık Kuvantum Tünellemesi (‘Quantum Tunelling’) yoluyla kuyu dışına sızabilirdi.’ denir. Doğrudur. Birazdan, bu fiziksel gerçeğin gözle görülür daha doğrusu kulakla işitilir örneklerini vereceğiz. ‘Ama, bu tünelleme olgusu sadece Kuvantum Fiziğine özgüdür. Klasik Fizik’te hiçbir örneği mevcut değildir.’ de denir. Oysa bu deyiş yanlıştır.
Telli çalgıların kirişleri, yani iki uçta telleri çalgı gövdesinin yukarısında tutan parçalar ve tellerin kendileri mükemmelen yalıtılmış olsalardı, tellerdeki titreşimler kirişlerden sızarak veya ses halinde çalgı gövdesine çarparak yeni tınılar oluşturamazdı. Bu da, ∞ kadar yüksek potansiyel kuyusuna iyi bir örnek teşkil ederdi. Ne ki, bu ek tınılar da kulaklarda ek tadlar, lezzetler yaratmaktadır. Bu nedenle örneğin Stradivarius kemanlar, Ovation gitarlar baş tacıdır.
Sonuç olarak, Pisagor’un telden çıkan sesin formülasyonu ile Schrödinger Denklemi’nin tam (analitik) çözüm verdiği dört olgudan biri olan ‘Sonsuz Potansiyel Kuyusu’ probleminin çözümü tıpa tıp aynıdır.
Belki, diyeceksiniz ki, “Az gittik, uz gittik…”
Bunda şaşıracak ne var ki?
Evet, Pisagor ve öğrencilerinin, bugün bize (en hafif deyimle) biraz tuhaf görünen bazı fikirleri paylaştıklarını biliyoruz. Örneğin, Pisagor ve öğrencileri her şeyin matematikle ilgili olduğuna, sayıların son gerçek olduğuna, matematik aracılığıyla her şeyin kestirilebileceğine ve ölçülebileceğine inanmışlardı. İki sayısı dişiliği ve doğanın bu dişilikten geldiğini ifade ediyordu, örneğin. Üç sayısı uyum ve düzenle maddenin içerdiği üçlü öğeyi temsil ediyordu. Bu sayı, başlangıcı, ortası ve sonu olan ilk rakamdı, yetkin bir sayıydı. Dört tanrısal gücü simgelerdi. İlk çift sayı olan “iki”nin kendisi ile çarpımından elde edilen bu sayı adaletin de simgesiydi. Beş sayısı evliliğin simgesiydi. Altı organik ve hayati varlıkların türlü şekillerini gösterirdi. Burada dişilik ilkesi olan (2), erkeklik ilkesi olan (3), mutlak (1) ile birleştiği için soyların devamını da gösterirdi. Yedi sayısı kritik sayıları temsil ederdi; yedi günlük, yedi aylık ya da yedi yıllık dönemlerin varlıkların gelişiminde baskın rolleri vardı. Sekiz sayısı akıl, ahlak ve erdemin temsilcisiydi. Dokuz sayısı mutlak Bir ayrı tutulacak olursa ilk tek sayı Üç’ün karesiydi ve bu sayı da adaleti temsil ederdi.
Ama asıl tuhaflık şurada değil midir?
Değil sadece Pisagor zamanında, çok daha öncesinde bile kuru dal parçalarını bir birine sürterek ve kolay tutuşan kuru ot, yaprak, liken vb. yardımıyla ateş yakılmıyor muydu? Günümüzde de, ucuna kolay tutuşan kimyasal bileşikler sürülmüş kibrit çöpleri kullanmıyor muyuz ateş yakmak için. Hadi olsun, bir metal çarkı kıvılcım çıkartmak amacıyla çakmak taşına sürttürüyor, o kıvılcımlarla kolay yanıcı bir gazı tutuşturarak çakmak yakıyoruz. En gelişmiş ateş yakıcı aletlerimiz ise, son beş on yıllarda yaygınlaşan mutfak ocaklarında gaz tutuşturmak amacıyla kıvılcım yaratan elektrikli manyetolar. Dikkat etmeye değer; günümüz nüfusunun büyük çoğunluğu kibrit kullanırken ancak gelişkin ülke beldelerinde elektrikli çakmak kullanılmakta. Bu mudur on bin yıllık insan gelişmişliği?
Hâl bu iken, niçin şaşmalı ki; Pisagor ile aynı yöntemi kullanarak ateş yakıyorken, onunkine benzer giysiler ve onunkine benzer pabuçlar giyiyorken matematiği de onun gibi evrenin asli unsuru sanıyor oluşumuza?
(*) https://www.google.com/search?q=T%C3%BCme+Var%C4%B1m+Y%C3%B6ntemi
(**) https://www.google.com/search?q=pisagor+%C3%BC%C3%A7l%C3%BCleri
Ayrıca; https://www.matematikdunyasi.org/1991/02/pisagor-teoremi-ya-oncesi/
Ayrıca; https://www.matematikdunyasi.org/pdf-arsiv/#flipbook-df_3127/23/
A²+B²+F²=G² eşitliğini sağlayan Dörtlükler de vardır ki, bunlar, kenar uzunlukları A, B, F ve G olan Dik Dörtgenler Prizmaları’nın gövde köşegen uzunluklarıdır. A²+B²+F²+H²=P² ise, Dört Boyutlu Dik Dörtgenler Prizmaları’nın gövde köşegen uzunluklarıdır. Bkz., https://www.google.com/search?q=4+boyutlu+k%C3%BCp
(***) George Gamow’un ‘1, 2, 3, … Sonsuz’ adlı kitabında (Bkz., https://www.google.com/search?q=George+Gamow%E2%80%99un+1%2C+2%2C+3%2C+%E2%80%A6+Sonsuz+ )sözünü ettiği Hotanto (Bkz., https://www.google.com/search?q=Hotanto&sca_esv=fc5970edc32ae20c&sxsrf=ADLYWIKCkeKsSIDHYxsXGP657h3YgN0aUw%3A1734562442919&ei=ilJjZ8rkN92Jxc8PoMXd8Qo&ved=0ahUKEwjK0YDStLKKAxXdRPEDHaBiN64Q4dUDCBA&uact=5&oq=Hotanto&gs_lp=Egxnd3Mtd2l6LXNlcnAiB0hvdGFudG8yChAjGIAEGCcYigUyChAjGIAEGCcYigUyBBAjGCcyBRAAGIAEMgUQABiABDIEEAAYHjIGEAAYBRgeMgYQABgFGB4yBhAAGAUYHjIIEAAYgAQYogRI5khQ4BlYwCpwAngAkAEAmAF-oAGLBqoBAzEuNrgBA8gBAPgBAZgCB6ACrwbCAgsQABiABBixAxiDAcICERAuGIAEGLEDGNEDGIMBGMcBwgIOEC4YgAQYsQMY0QMYxwHCAggQABiABBixA8ICChAuGIAEGEMYigXCAg0QABiABBixAxiDARgKwgIFEC4YgATCAggQLhiABBixA5gDAIgGAZIHAzEuNqAHt1M&sclient=gws-wiz-serp ) dilinde ‘1, 2, 3, çok’ gibi sadece 4 tane nicelik yeterli olmuş.
(****) https://translate.yandex.com/?utm_source=yandex&utm_medium=com&utm_campaign=morda&source_lang=la&target_lang=tr&text=finitum
(#) https://tr.wikipedia.org/wiki/Dize_titre%C5%9Fimi
https://acikders.ankara.edu.tr/pluginfile.php/189894/mod_resource/content/1/SES%20DALGALARI%2C%20REZONANS%20OLAYI%2C%20B%C4%B0LE%C5%9E%C4%B0K%20SESLER.pdf
Ayrıca; https://www.youtube.com/watch?v=gsWRPpDlt9Y
Ayrıca; https://muzikuniversitesi.com/gam-nedir-gitarda-gamlar-nasil-ogrenilir/
(##) https://tr.wikipedia.org/wiki/Galileo_Galilei
(###) Katıda ses hızı: 1. Dkk. İtibaren https://www.google.com/search?q=maddei%C3%A7inde+ses+h%C4%B1z%C4%B1&sca_esv=189649982420d558&sxsrf=ADLYWIJRPaCopDTLLVj3pr9mX2U0QDVSIg%3A1734164456857&ei=6D9dZ7-ANLGIxc8P5MbRmAs&ved=0ahUKEwi_lLuD6qaKAxUxRPEDHWRjFLMQ4dUDCBA&uact=5&oq=maddei%C3%A7inde+ses+h%C4%B1z%C4%B1&gs_lp=Egxnd3Mtd2l6LXNlcnAiF21hZGRlacOnaW5kZSBzZXMgaMSxesSxMgcQIRigARgKMgcQIRigARgKMgcQIRigARgKMgcQIRigARgKSNuJAVDlEFjlgQFwAXgBkAEAmAGTAaABqB-qAQQxLjMzuAEDyAEA-AEBmAIUoAKoEsICChAAGLADGNYEGEfCAgcQIxiwAhgnwgIIEAAYogQYiQXCAggQABiABBiiBMICBRAAGO8FwgIKECEYoAEYwwQYCpgDAIgGAZAGCJIHBDEuMTmgB6WzAQ&sclient=gws-wiz-serp#fpstate=ive&vld=cid:75e94f95,vid:xMEKCLDVRIg,st:0
Ayrıca bkz., https://en.wikipedia.org/wiki/Speed_of_sound

(####) https://www.google.com/search?q=sonsuz+potansiyel+kuyusu