İçerik: Geçmişe mazi derler; belgesi, kaydı kuydu falan varsa tarih derler.
Fizik –15 / d–
‘İnsanın düşüşü’ Fizik’in konusu değildir henüz; çünkü, insanın düşüşünün deney ve gözlemlerini yapamadığımız gibi, yapsak bile elde edilecek verinin nasıl değerlendirileceğini bilmiyoruz henüz.
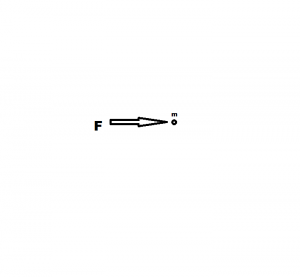
Benzerleriyle etkileşmeyen noktasal bir kütleye etkiyen kuvvet altında nasıl hareket edilecek olduğunu biliyoruz ama ‘benzerleriyle etkileşmeyen noktasal bir kütle’ bulamıyoruz evrende. Dolayısı ile, ‘benzerleriyle etkileşmeyen noktasal bir kütle’nin devinim denklemlerini elde etsek ve onların sözcüğün tam anlamıyla ‘deterministik’ olduğunu bilsek bile, ancak şu ya da bu denli yaklaşık sonuçlar elde edebiliyoruz.
Dahası, elimizdeki Fizik yasaları, evrendeki olayların çok küçük bir kısmına ilişkin. Hani derler ya, ‘okyanusta bir damla’; o kadar. O kadar bile olmayabilir; evrendeki her olayı da algılayabiliyor, her olayın farkında olabiliyor da değiliz aslında. Bu zayıflığın en tipik göstergelerinden biri bizatihi Fizik’in gelişim hızı. Bakınız mesela, ilk Fizik yasalarını ortaya koyan Arşimet –bu yasalar statik olaylara ilişkindi– ile ilk devinim yasalarını ortaya koyan Galileo_Newton arasında yaklaşık 1800 yıl var. Ama, arada başka Fizik yasası yok. İlginç değil mi; Newton günlerinde bile Fizik’in adı bile yoktu ortalıkta?!
İyi de, Arşimet ile Newton arasındaki sürede hiç mi buluş yapılmadı Fizik’le ilişkili olan?
Yapılmaz olur mu? Hiç durmaz ki, buluşlar; her an her konuyla ilişkili bir buluş yapıladurur. Çevresine şöyle bir bakan herkes görür ki, gördüğü her nesne bir süre öncesinin buluşudur. Öte yandan, Arşimet’in, yanlış bir adlandırmayla, ‘Suyun Kaldırma Kuvveti’ diye bilinen yasası bulunmazdan evvel de gemiler yüzüyor, ‘Kaldıraç Yasası’ bulunmaz evvel de kayık ve gemilerde kürek kullanılıyor, ağır nesneler kaldıraç sayesinde kaldırılıyordu yukarı. Örneğin, Mısır piramitlerinin inşasında yaygınca kullanılmışlardı.
Gelgelelim, Fizik ne denli eksikli olursa olsun, Fizik’siz yapamayız. Eksikli ve zayıflıklı şimdiki hali ile bile neler başarıldığını tek tek saymak kimbilir kaç sayfa doldurur.
Elbette, insan geliştikçe Fizik de gelişecektir. Örneğin, insan anlağı, zaman içinde değişen kuvvetlerin önemini kavradığında Galileo denklemlerinden çok daha yetkinlerine kavuşacağız. Bunun yanı sıra, nesneler ile sebep-sonuç ilişkileri hakkında daha gelişmiş bulgulara gereksinimimiz olduğu açık. Örneğin, herhangi bir sonucun sebebi değil sebepleri, sebeplerinin hepsi ayrıştırılmış olmalıdır. Bu da hiç kuşkusuz, insan anlağının gelişkinliğine yakından bağlıdır.
Örneğin, bir futbol maçının sonucunun bir taneden çok daha fazla mı sebebi olduğu, yoksa –hadi diyelim en belirleyicisi olan– bir tek taneye mi indirgenebileceğinden emin değiliz henüz. Kaldı ki, 90 dakikalık bir futbol maçını bile tüm incelikleriyle birlikte izlemekten, gözlemekten mahrumuz henüz.
Özetle, kaplamı olmayan noktasal parçacıklar, kaplamı olmayan iki noktasal parçacık arasındaki etkileşimden kaynaklı devinimlere ilişkin tek sebep tek sonuç bağlamındaki bilgi dağarcığımızda etkileşmelerin nasıl oluştuğunu bilmediğimiz gibi, noktasal parçacıklara ait kütlenin de ne olduğunu bilmiyoruz. Bu etkileşme ve devinim dışındaki her şeyin aynı kaldığını varsayıyoruz. İşte bu daracıklıkta da Fizik’i geliştirmeye çalışıyoruz.
Futbol maçları da eni konu birkaç yüz metre karelik bir alancıkta yapılıyor, 22 kişi bir tek top peşinde koşturuyor ve o topa her vurulduğunda bir yeni devinim oluşuyor. Ama, Futbol Fizik’imiz yok henüz. Çünkü, futbol maçında tek sebep-tek sonuç bağıntısı çalışmıyor. Topa vuruldukta, diğer her şey aynı kalmıyor. Daha pek çok gerekçe de ileri sürülebilir bu konuda.
Bütün bunlardan sonra, bir de, 90 dakikadan çok daha uzun süreli olan tarih konusunda çok daha umutsuz olduğumuz düşünülebilir. Ama bu bir yanılgıdır. Çünkü, yakın ileride haylice konu edeceğimiz gibi, Tarih’in yasaları vardır.
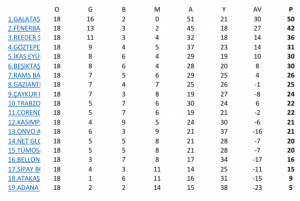
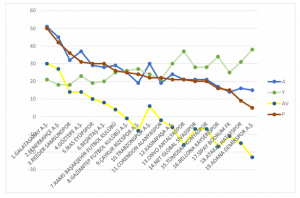
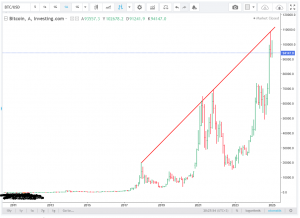
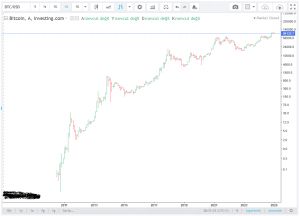
Bu son cümleyi yadırgamış olanlar için Tarih’in kıyısından bir örnek vermek uygun olabilir. Bilindiği gibi, enerjisi E frekansı da 1/τ olan dalga için Einstein kuvantum bağıntısı ile doğrusal momentumu P, dalga boyu da λ olan dalga için De Broglie bağıntıları şöyle yazılabilir; Eτ=Pλ=h (=Planck Sabiti). Bunun gibi, şu anki dağılımda tüm ülkeler genelinde nüfusu N kadar (N ile ΔN arasında) olan kent, kasaba gibi yerleşke sayısı n ise, şu bağıntı empirik olarak saptanmış durumdadır; Nn=1. Yani, nüfusu N kadar olan n kadar yerleşke varsa, nüfusu N’ kadar olan n’=(N/N’)n kadar yerleşke vardır.
İşitir gibiyim; ‘İyi de, bir üst paragraftaki Pareto_Zipf yasası (*) Tarih’e değil, şimdiki zamana ve demografiye ait.’
Öyle olsa bile, aynı dağılım geçmiş zaman içinde oluşmadı mı? Ayrıca, geçmiş zamanda yani Dünya nüfusu bugünküne kıyasla çok daha az olduğu zamanlarda yerleşke nüfusu ve sayısı arasındaki ilişki acep aynı mı idi? (**)
Tarih’in daha az itiraz edilebilir ve hatta hiç itiraz edilemeyecek olan yasalarından da söz edeceğiz.
(*) https://www.google.com/search?q=Pareto_Zipf+yasas%C4%B1
(**) i) arXiv:0802.4064 A theoretical approach for Pareto-Zipf law Authors: Caglar Tuncay
Abstract: We suggest an analytical approach for Pareto-Zipf law, where we assume random multiplicative noise and fragmentation processes for the growth of the number of citizens of each city and the number of the cities, respectively.
ii) arXiv:0710.2023, Model of World; her cities, languages and countries Authors: Caglar Tuncay
Abstract: The time evolution of Earth with her cities, languages and countries is considered in terms of the multiplicative noise and the fragmentation- processes, where the related families, size distributions, lifetimes, bilinguals, etc. are studied. Earlier we treated the cities and the languages differently (and as connected; languages split since cities split, etc.). Hence, two dis- tributions are ob… ▽ More
iii) https://www.tandfonline.com/doi/abs/10.1080/00222500212987 The nonlinear and scaled growth of the ottoman and Roman empires, Güngör Gündüz.
Abstract
In this work, mathematical models for the growth of the Ottoman and Roman Empires are found. The time interval considered for both cases covers the time from the birth of the empire to the end of the fast expansion period. These empires are assumed to be nonlinearly growing and self-multiplying systems. This approach utilizes the concepts of chaos theory, and scaling. The area governed by the empire is taken as the measure of its growth. It was found that the expansion of each empire on lands, seas, and on both (i.e., lands+seas) can be expressed by power laws. In the Ottoman Empire, the nonlinear growth power of total area is approximately equal to the golden ratio, and the nonlinear growth power of the expansion on lands is approximately equal to the square root of 2. In the case of the Romans, some numbers associated with the golden ratio, or the square root of 2, appear as the power of the nonlinear growth term. The appearance of both the golden ratio and the square root of 2 show that both empires had intention on achieving stability during their growth.
Yukarıdaki makalelerdeki referanslara da bakılabilir, https://arxiv.org/ arama motorundan da yararlanılabilir, https://www.jstor.org/ arama motorundan da.