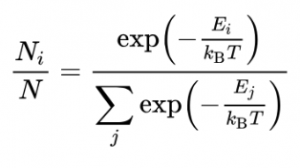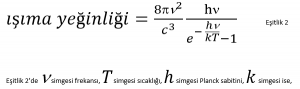FİZİK -4 / a-
İçerik: Zeno, Maxwell, Boltzmann, Einstein, fırın, karacisim ve azıcık matematik
Zeno’dan Einstein’a gelen kuvantum yolu James Clerck Maxwell ile Ludwig Eduard Boltzmann’a uğrar. Kapalı, yani dışı ile etkileşimi sıfır olan bir sistem içindeki toplam olarak N_tane noktasal parçacıktan, enerjisi Ei olan ‘microstate’ kapsamında Ni tane noktasal parçacık varsa, bu parçacıkların dağılımı alttaki Maxwell-Boltzman formülü ile tanımlanır. (*) Bu formülün paydasındaki J indisi parçacıkların her birini sayar. Dikkate değer, N sayısı bilinen herhangi bir doğal sayıdır; açıkçası, sonsuz (adet tanecik olamayacağı olmadığı için) değildir.
Gelgelelim, pek çok olguyu açıklamakta kullanılan bu temel formülün çok sıradan, her gün herkesin rastladığı rastlayabileceği bir olguyu açıklamakta yetersiz kaldığı çok geçmeden anlaşıldı.
Hemen her evde bir elektrikli fırın vardır. Hemen her evin yakınlarında da bir simit veya ekmek fırını vardır. Bu fırınların ortak özelliklerinden biri şudur: Her fırının içindeki sıcaklık dört yüz Celsius derece kadar olmasına karşın, fırının gözleme penceresi veya kapağı açıldığında bakanı hemen hiç rahatsız etmez. Çünkü o mertebede ısı çıkmaz o aralıktan. Bu tür, yani sahip olduğu enerjiyi yayımlamayıp yahut en fazlası çok küçük bir orandakini yayımlayan nesnelere KARACİSİM denir.
Bu karacisimlerin bir ortak özelliği de şudur: yaydıkları ışımanın içinde her frekanstan (her dalga boyundan dense de doğrudur) ışın vardır.
Şöyle düşünelim. Diyelim ki, bir mikrodalga fırını sabit bir frekanstan ısıtma yapıyor. Yani, fırına gelen elektrik, ısıtıcıyı sabit bir frekansta titreştirip bu frekansta ışıma yayılmasına sebep oluyor. Bu mikrodalga fırının kapağı açılıp çıkan (sızan dense de olur) ışımanın frekans dağılımı (izgesi, ‘spectrum’) incelendiğinde şu görülür: Fırın ısıtıcısının titreşim frekansını da içeren velâkin tüm frekanslarda ama yeğinliği (‘amplitude’) frekansa göre değişim gösteren bir dağılım gözlenir.
Oysa, J. C. Maxwell’in büyük katkılarıyla geliştirilen (Klasik) Elektromıknatıslık Kuramına göre tek frekansta (ısıtıcı frekansı) ve bu frekans değiştirilse bile bu frekansın karesi ile orantılı enerji yayılımı gözlenmesi gerekiyordu. Dahası, bu enerji yayılımı, mor ötesi frekansları gibi, X-ışını ve hele gamma-ışını frekansları yanında önemsenmeyecek denli küçük olan frekans değerlerinde bile, Dünya’da üretilemeyecek büyük miktarlarda enerjiye denk gelmekteydi. İşte bu çelişkiye de mor ötesi yıkım (‘ultraviolet catastrophe’) denmişti. Yıkım (‘catastrophe’) sözcüğü ile şu ima ediliyordu sanki: Maxwell kuramı yanlış mı veya hiç değilse eksik miydi acaba?
Bu soru uzun yıllar belini büktü fizikçilerin.
İlkin, tüm karacisimlerin enerji-frekans izgelerinin benzeş olduğu farkedildi. Çok düşük frekanslarda, frekansın karesi ile (parabolik) büyüyen enerji böyle devam etmiyor ama bir zirve yapıp büyük frekanslarda giderek azalıyordu.
Garip! Büyük frekanslarda ışıma enerjisi frekans ile artmıyor, tersine azalıyordu.
İkincileyin, bu gözlemsel karacisim ışıma izgesinin matematiksel formülü benzeştirme (‘fitting’) yöntemiyle elde edildi. Frekansa bağlı ışıma yeğinliğini veren formül şu şekildeydi:
Eşitlik 2’de simgesi frekansı, Tsimgesi sıcaklığı, h simgesi Planck sabitini, k simgesi ise, Boltzmann sabitini göstermektedir. İlgili grafik de şu bağlantıda incelenebilir: https://www.google.com/search?q=karacisim
Böylelikle ‘morötesi yıkım’ sorunsalı Eşitlik 2’deki formülün nasıl elde edileceği sorunsalına indirgenivermişti. Pek çok fizikçi ve pek çok matematikçi pek çok çeşitli simgelerin pek çok kombinasyonunu denedi o formülü elde edivermek için.
Öyle ya, ucuz malzemelerden altın elde etmeye çalışmış olanlar da aynı yöntemi izlememiş miydi? Isaac Newton da o ünlü kütleçekim formülünü (Mm/r2) elde etmek için önce bu çekimin sadece ve sadece cisimlerin kütlelerine ve aradaki uzaklığa bağlı olacağını varsayıp bu üç simgenin yerleriyle oynayarak Kepler Yasaları’nın üçünü birden veren o formülü deneyerek bulmamış mıydı? Bkz., Isaac Newton: The Principia, Mathematical principles of natural philosophy, a new translation” by I Bernard Cohen and Anne Whitman, preceded by “A Guide to Newton’s Principia” by I Bernard Cohen, University of California Press, 1999.
Gelgelelim ne denense olmuyordu taa ki, rivayete göre, Boltzmann’ın son derece önemli bir fikri Planck’ın kulağına fısıldayana dek. O müthiş büyük, çağ değiştirici fikir şuydu: Enerji sürekli olmayıp paketçikler halindedir.
Başka bir deyişle, sıcak cisimlerin yaydığı ışımadaki fotonların enerjisi sürekili olmayıp basamaklı yani paketçikli (‘quantised’) haldedir.
Bu fikrin ortaya çıkışından sonrası kolaydı.
İlkin, serbest bir fotonun enerjisi E=Planck sabiti çarpı frekans olarak tanımlandı. Hemencecik ardından da, T sıcaklığındaki kapalı bir (yani, yalıtılmış ve dışarı enerji ve parçacık sızdırmayan veya bu sızıntının ihmal edilebilecek denli küçük olduğu) sistemdeki fotonların paketleneceği ve her birinin enerjisinin, n bir doğal sayıyı göstermek üzere En=nxhxfrekans biçiminde yazılabileceği varsayıldı.
Acaba, bir fırının içindeki fotonların adedi sayılabilir mi? Sayılamaz elbette, hani ‘sonsuz’ denir ya o kabilden. (**)
Peki ya ‘sonsuz’ foton içeren fırında yeni fotonlar üretilebiliyorsa? İşte bu soruyu sormakta iseniz, Hilbert’in Sonsuz Oteli’ndesiniz demektir. “—Hoş geldiniz!” Bir koltuğa veya kanepeye kurulup veya yatağınıza uzanıp 1, 2, 3, … SONSUZ başlıklı yazıyı okuyabilirsiniz. Bkz., https://blog.metu.edu.tr/caglart/?s=Hilbert
Herhangi bir enerji değerine sahip foton sayısının belirsizliği nedeniyle bu yazının tepesindeki Eşitlik 1’in fotonlar için revize edilmesi gerekmekteydi. Bunu da, devamı olan Zeno-Planck-Einstein ilişkisine de bir sonraki Fizik – 4 / b- Zeno’dan Einstein’a Kuvantum yazımızda değinelim.
(*) https://en.m.wikipedia.org/wiki/Maxwell%E2%80%93Boltzmann_distribution
https://www.gtu.edu.tr/Files/UserFiles/90/MF1-KARA_CSM_IIMASI.pdf
(**) ‘Sayılabilir sonsuzluk’ (‘countable infinity’) ile ‘sayılamaz sonsuzluk’ (‘uncountable infinity’) konusunu tartışmayı bir başka yazıya bırakıyoruz.