Monthly Archives: August 2025
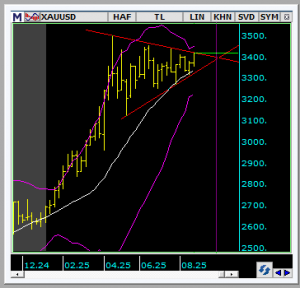
NOT 57 ONS ALTIN (XAUUSD) fiyatları
Matematik’te ve Felsefe’de Evrensel Set -4-
Diyelim ki, günlerden Pazartesi ve 3000 odalı bir Hilbert Oteli’nde 1 misafir kapı numarası 1 olan odada konaklamakta. Salı günü 1000 yeni misafir gelirse, konaklayabilirler. Çarşamba günü 1000 yeni misafir gelse bile tüm misafirler konaklayabilir. Peki, Perşembe günü de 1000 yeni misafir gelirse ne olur?
Sonsuz Odalı Hilbert Sonsuz Oteli’ndeki gibi tıpkı; her misafir bir büyük kapı numaralı odaya kaydırılır. Böylelikle, tüm misafirlerin otelde barınması sağlanabilir.
Ne ki, dikkatli okuyucu fark etmiştir ki, otel koridorlarında hareketlilik asla durmayacaktır. Tıpkı, Sonsuz Odalı Hilbert Sonsuz Oteli’ndeki gibi.
Bitti.
Matematik’te ve Felsefe’de Evrensel Set -3-
“Düşünüyorum; demek ki, varım.” önermesi doğru olsa bile, düşündüğüm her şey var olmayabilir; “Evrensel Set düşünüyorum; demek ki Evrensel Set var.” önermesi gibi.
Ara saptama; olmayan şeyleri de düşünebiliyorum. Bir başka örnek şudur; gerçeklikte var olmayan rüyalar görebiliyorum!
Bu durumda, “Düşünüyorum; demek ki, varım.” önermesinin doğru olduğunu iddia edemem.
Devam edeceğiz.
Matematik’te ve Felsefe’de Evrensel Set -2-
Evrenin ne(ler)den yapılı olduğunu bilmiyoruz. Dolayısı ile, evren elementleri olup olmadığını da bilmiyoruz. Ama, zihin jimnastiği yapmanın herhangi bir (ciddi) sakıncası olmadığına göre, evrenin birbirinden ayrık ve dolayısı ile sayılabilen ve dahası değişmez (‘stable’) elementlerden (=içeriklerden) oluştuğunu varsaymanın da sakıncası yoktur.
Bu durumda evreni bir set (E) ile temsil edebiliriz;
E=[e1, e2, …, eN] .
Evren içeriklerini, unsurlarını sayılabilir diye kabul ettiğimiz için N bir Artılı Tam Sayı (Doğal Sayı) olmalıdır. (Yani, N ‘finite’ olmalıdır.) Dahası, E kendini içeremez çünkü E (gerçek) evrene ait değildir, hayâl alemine aittir.
Dikkatli okuyucu fark etmiş olmalı ki, evren elementlerinin birbirine dönüşmediğini varsaydık. Bu da ‘N sayısı sabitir.’ demektir.
Eğer evren içerikleri birbirine dönüşüyor, evriliyor ise Evrensel Set’imiz E’nin de zamanla değişmesi gerekir. Bu koşul altında E(t)←E ve N(t)←N yazılması gerekir.
Devam edeceğiz.
Matematik’te ve Felsefe’de Evrensel Set -1-
Ön not: Konunun ilgilisi hayli uzun bir kaynakça listesine sahiptir elbet. Yeni ilgilenebilecek okuyucu ise, şu iki toplu kaynaktan seçim yapabilir. (*)
Önceki pek çok yazımızda çeşitli sözüm ona paradokslara değinmiş idik. Örneğin Zeno Paradoksları’nda, görünüşteki zorluğun tamamen sözcüklerden kaynaklandığını değerlendirmiştik. İkinci örnek olarak değerlendirdiğimiz Hilbert’in Sonsuz Oteli (**) konusu hakkında da pek çok hem de pek eğlenceli kaynak mevcuttur. Asla yapılamayacak olan, yapılmasının mümkün olmadığı bir sözüm ona sonsuz odalı otel hakkında ahkâm kesmenin tadına doyulabilir mi?
Başka herhangi bir kişinin üstünde durduğuna şahit olmadığım bir soruya burada yer vereyim. Oda sayısı sınırlı, yani oda sayısı (diyelim ki, 100’den veya 1000’den yahut 10000’den) herhangi bir Tam Sayı’dan küçük ama alanı sonsuz olan hayali bir otele gelen misafir sayısı bilinen her Tam Sayı’dan büyük (yani, yaygınca kullanılan sözcükle ‘sonsuz’) olsaydı ne yapmak gerekirdi; tüm misafirlerin o otel odalarında konaklamasını sağlamak için?
Biraz daha açalım.
Diyelim ki, 10000 odalı böyle bir otelde 100 misafir konaklamakta. Ertesi gün 1000 misafir daha geldi. Ama, bir sonraki günde ‘sonsuz’ misafir geldi. (Sonsuz sayı değildir. Bu nedenle de şu ifade yanlıştır, anlamsızdır: “Ama, bir sonraki günde ‘sonsuz’ sayıda misafir geldi.”)
Bu son gelen misafirlerin bu otelde konaklamasını sağlamak mümkün müdür?
İPUCU: Bu sorunun yanıtı, Hilbert Oteli’nin çözümüne gider.
Gelgelelim, Hilbert Oteli’ni çözmeye çalışmak da eskilerin deyimiyle, abesle iştigaldir. Zira, Hilbert Oteli (gerçek) evrenin parçası, unsuru değildir; eskilerin deyimiyle ‘hayâl âlemi’ne aittir.
(*) https://plato.stanford.edu/search/searcher.py?query=frege
https://plato.stanford.edu/search/search?query=universal+set
https://www.jstor.org/action/doBasicSearch?Query=frege&so=rel
https://www.jstor.org/action/doBasicSearch?Query=universal+set&so=rel
(**) https://www.youtube.com/watch?v=1DdN-RXSSlo
Devam edeceğiz.
NOT 56 ONS ALTIN (XAUUSD) haftalık
grafiğinde fiyat çubukları ile 20 haftalık basit hareketli ortalama çizgisi (BOLLİNGER Bant ortası) arasındaki ilişkiyi yakından incelemek hayli kazanç sağlayabilir.
İPUCU: Neredeyse 2023’den bu yana fiyatlar, yukarıda belirtilen ortalamanın altında seyretmemiş.
NOT 55 Alım amaçlı olarak
Lattice Semiconductor Corp. NASDAQ: LSCC şirketi yakından incelenmeye ve izlenmeye değer doğrusu.
NOT: Televizyondaki yaygınca izlenen ekonomi-finans içerikli programlardan birinde önerildi.
NOT 54 Elimde BTCUSD yok. Ama,
olsaydı; $120k üstü veya oraları görmeksizin $110k altına düşerse tereddütsüz satardım.
NOT: Bu konuda herhangi bir duyumum falan yok.
NOT 2: BTCUSD (ve diğer kripto araçları) ile pek de ilgili olmadığım, ilk yüklemedeki fiyat yanlışlıklarından belli. Şimdi düzeltildi.
NOT 53 Finansal okumaz yazmaz Mahmut çiziktiriyor mu ABD’de de?
Olabilir! ABD hisse senetlerinin grafiklerini gösteren platformlara girilir; özellikle inşaat, enerji gibi alanlarda iş yapanlar seçilir. Örneğin BUILDING sözcüğü imlece ‘save’ edilir ve uygun grafikler seçilip değerlendirilir.