FİNANS FİZİĞİ -19-
Bakınız, çeşitli fiyat zaman serilerinden, örneğin NASDAQ 100 vadeli endeksinden başka ve hayali fiyat grafikleri nasıl elde edilebilir, örnekleyelim?!
GCM’nin veri deposundan NASDAQ 100’e ait günlük açılış (O), yüksek (H), düşük (L) ve kapanış (C) değerlerini tarih sırasıyla indirelim. Bu veri setini, ilk beş satırı boş bırakılmış bir Excel çalışma sayfasına da tarih, O, H, L ve C olmak üzere sırayla A, B, C, D ve E sütunlarına yerleştirerek, bu yazıda kullanacağımız zaman serilerini elde edelim. Altıncı satırın A, B, C, D ve E sütunlarında sırayla tarih, O, H, L ve C yazısı olsun. F sütununa
=(C6-B6)/B6
formülü ile hesaplanmış ve sonra alta doğru kopyalanmış günlük en fazla bağıl yükseliş değerlerini yerleştirelim. G sütununa
=(B6-D6)/B6
formülü ile hesaplanmış ve sonra alta doğru kopyalanmış günlük en fazla bağıl düşüş değerlerini yerleştirelim.
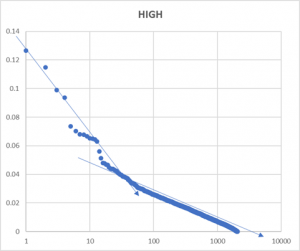
Şimdi de, H sütununa 6_ıncı satıra 1 yazarak alta doğru 1’er artırıp (H7=H6+1), (H8=H7+1), … gibi, bir sıra sütunu elde edelim. I sütununa ise, F sütunundaki değerleri nümerik (nominal) olarak kopyalayalım. Sonra da, H ve G sütunlarındaki değerleri G sütunundaki değerler büyükten küçüğe sıralayıp çerçeveledikten sonra EKLE–>ÖNERİLEN GRAFİKLER–>TÜM GRAFİKLER’den (X.Y) DAĞILIM’ı seçip ilk grafiğimizi (GRAFİK 1) elde edelim. GRAFİK 1 giderek azalan bir çizgi verecektir. Yatay ekseni LOGARİTMİK yaptığımızda alttaki görünüşü elde ederiz ki, burada küçük değerler için üslü (‘exponential’) azalış düzenliliği bağıl olarak büyük değerler ise rassal azalış gösterdiği açıkça görülebilir.
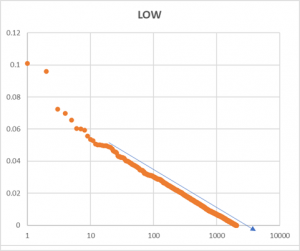
Aynı yaklaşım, en çok düşüşler için de kullanıldığında GRAFİK 2 elde edilir.
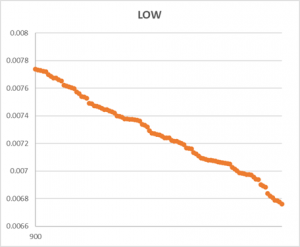
GRAFİK 1 ve GRAFİK 2’de azalış düzenliliği zahiridir (sanki, görünüşte, ‘apparent’). Örneğin, GRAFİK 2’deki logaritmik yatay eksen 900 ile 1000 arasına, dikey eksen de 0,0066 ile 0,0080 arasına alındığında GRAFİK 3’deki gibi bir rassallık açıkça gözlenebilir.
Gelgelelim, H sütunundaki veri daha az önemli değildir. Herhangi bir gün içi en büyük yükselişin hangi sıradaki gün içinde oluştuğu bilgisini taşımaktadır. Bu yazıda 26.07.2017 işlem gününden bu yazının yazılmaya başladığı tarih olan 17.06.2025’ye dek 2055 güne ait veri seti kullanılmıştır ve örneğin GRAFİK 1’deki en büyük gün içi yükseliş 2007_inci günde yani 09.04.2025 tarihinde gerçekleşmiştir. H sütunundaki sayıların 1’den 2055’e dek birer birer değiştiği dikkate şayandır. Aynı sayıların 0 (hariç) ile 2055 arasında rassal düzgün (‘homogeneous’) dağılım gösterdiği de dikkate şayandır. Aksi durum, manüplatif işlemler yapılmış olduğunu ima eder.
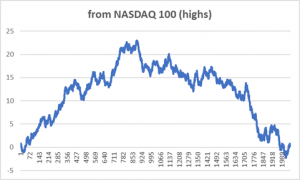
Şimdi de aynı yani H sütunundaki sayıları 2055’e bölüp J sütünuna yerleştirerek 0 (hariç) ile 1 arasında rassal düzgün (‘homogeneous’) dağılan bir dağılım elde edelim. Bu sayılardan yani J sütunundakilerden 0,5 çıkarıp K sütununa yazalım. K sütunundaki serinin integralini de L6=K5+L6 formülün kullanıp alta doğru kopyalayarak alalım ve L sütununa yazıp grafiğini çizelim. Sonuç bir fiyat grafiğinin benzeri çıkacaktır, azalan/artan eğilimler, yerel tepeler, yerel dipler vd. içerebilen. Bkz., GRAFİK 4.
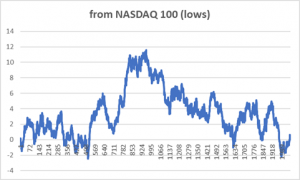
Hemen yukarıdaki yaklaşımı (Open-Low)/Open formülü kullanılarak elde edilmiş günlük bağıl düşüşler için de uygulayabiliriz. Bkz., GRAFİK 5.
GRAFİK 4 ve GRAFİK 5’i beğenmez olursanız da ilgili sütunları, örneğin L sütunundakileri rassal olarak karıp (‘shuffling’) yeniden grafik çizdirebilirsiniz.