Fizik – 7 –
İçerik: Sizin dalgaboyunuz ne kadar?
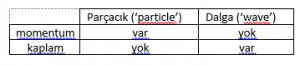
Tarihsel silsile içinde, önce Planck (ve Boltzmann (?)) ışık enerjisinin Planck sabiti (h) ve dalga frekansı (f) çarpımına eşit olduğunu ileri sürüp kanıtlamışlardı. Sonra Einstein geldi ve Fotoelektrik olgusunu açıklamak için, ışığın doğrusal momentumunun da (p) olduğunu ileri sürdü. Bu tez, başka hiçbir kuramla açıklanamayan Fotoelektrik deney sonuçlarını tamamen açıklıyordu. Einstein, 1905 yılında bu momentumun değerinin p=E/c olduğunu da kanıtladı. Böylece, ortaya gerçek bir paradoks çıktı. Çünkü, o zamanki bilgiye göre, parçacığın iki özelliği doğrusal momentum (=kütle çarpı doğrusal hız) sahibi olması ama uzayda herhangi bir en, boy, derinlik gibi kaplamının (‘extension’) olmayışıdır. Buna karşılık dalganın iki özelliği ise, tam tersine, uzayda yayılması ve dolayısı ile kaplamının olması ama kütlesinin olmayışı nedeniyle doğrusal momentumunun olmayışıdır.
Her ne kadar, 1000 yılı dolayında yaşamış Müslüman bilimciler, bugün Geometrik Optik diye bilinen her şeyi keşfetmiş ve kitaplara nak’şetmişlerdi. I. Newton da, ışığın top mermileri gibi dümdüz giden parçacıklardan oluştuğunu kitabında (*) yazmıştı. Ama, özellikle Christiaan Huygens’in ve Augustin-Jean Fresnel’in deneyleri ve tezleri, ışığın dalgalı ırasını (karakterini), doğasını (naturasını) kuşkusuz bir şekilde insanlığın bilim dağarcığına katmıştı. Işık dalgaları da uzayda, tıpkı su dalgalarının suda yayıldığı gibi yayılmaktaydı. Örneğin ışık, çift yarıktan geçerken, her dalganın yaptığı gibi, girişim saçakları oluşturmaktaydı.
İşte bu kuşkusuzluğu Einstein’ın p=E/c denklemi epeyce sarsmıştı. Demek ki, madde ile etkileşmez sanılan ışık, momentuma sahip olması nedeniyle maddeyi apaçık bir şekilde etkileyebiliyordu.
Dahası, E=hf bağıntısı kullanılarak, Einstein denklemi, d simgesi dalga boyunu temsil ederek, p=hf/c=h/d haline dönüşmekteydi. Çünkü, her dalga için, v dalga hızı olmak üzere, d=v/f idi.
Epey ilginç, değil mi!? Işığın dalgaboyu ile momentumunun çarpımı sabit idi ve bu değer tam da Planck sabitine eşitti.
Şaşkınlık uzun sürdü.
Gel zaman git zaman bu konuda yaprak kımıldamadı adeta. Ta ki, Fransa’nın Broglie yöresi dükü olan Louis-Victor Pierre Raymond, p=h/d eşitliğini, d=h/p şeklinde yazana dek, 1924-1927 arasında. Yazınca ne mi oldu?
Yer yerinden oynadı adeta ve kuvantum fiziği ortaya çıktı. Oysa, başarılan iki simgenin yer değiş_TİRİL_mesiydi aslnda; hani şu bayağı kesir işlemlerindeki içler dışlar çarpımı konusu.
Herşey bu denli yalındı; Einstein eşitliğindeki p paydaya gitmiş, yerine paydadaki dalga boyu simgesi gelmişti. Hepsi hepsi bu kadardı işte! Hani güzel Türkçe’mizdeki şu deyim bir kez daha doğrulanmıştı adeta: “Ha Ali Veli, ha Veli Ali!”
Lâkin, “Veli’nin kerrakesi” pek de öyle değildi. Matematikle oynamak çocuk işi de gerçek neydi, nasıldı acaba? Hem aynı yer değiştirmeyi Planck, Boltzmann, Einstein ve diğer ulular niçin başar_A_mamıştı? Akıl mı edememişlerdi?
Zinhar hayır! Mutlaka akıl etmişlerdi ama bu tezi ileri sürebilmek için ellerinde herhangi bir görgül (‘empirical’) olgu yoktu. De Broglie’nin ise, ağabeyi Maurice de Broglie’nin (**) zamanına göre hayli gelişkin olan bir fizik laboratuvarı vardı ve burada birlikte yaptıkları Röntgen’in X-Işınları ve Einstein’ın Fotoelektronları üstündeki deneysel ve kuramsal çalışmaları bilim dergilerinde yayınlanmıştı. Aynı laboratuvarda çeşitli parçacıkların örneğin elektronların çift yarıktan geçerken oluşturdukları girişim saçaklarını ve bu saçakların dağılımından da elektronların hızına bağlı olarak dalgaboylarının nasıl değiştiğini ve sonuçta m kütle ve v doğrusal hız simgesi olmak üzere hep (h/p)=h/(mv) bağıntısına uygun dalgaboyuna sahip olacak şekilde davrandıklarını deneyle saptamış olmalılar.
Yirmi yıl kadarlık bir arayla da olsa, ardı ardına geliveren bunca büyük buluş, pek çok insanın da aklını karıştırıverecekti elbette. Örneğin, işbu yazının tamamlandığı gün internette varlığını sürdürmekte olan şu söz külliyen yanlıştır: “Hareket eden bir parçacığa bir dalga eşlik eder hipotezi Louis de Broglie’ye aittir.” https://tr.wikipedia.org/wiki/Louis_de_Broglie
Yani, “bir parçacığa” dalga eşlik etmez. Hareketli bir parçacığın bizatihi kendisi dalgadır da. Onun tanecik özelliklerini yani kütle ve hızını ölçmek için, momentum alışverişinin (etkileşiminin) yer aldığı bir deney yaparsınız. Yok eğer, dalga özelliklerini ölçek amacındaysanız da, çift yarık ve benzeri dalgaboyu, frekans ve benzeri dalga değerlerini açığa çıkaracak bir deney yaparsınız.
Kan değerlerini ölçmek için tıp merkezlerinde kan alınır, sindirim bozukluklarını saptamak için ise, başka tür tahliller yapılır.
Veya daha yalını; ağırlığınızı öğrenmek için tartı aletine, basküle çıkarsınız; boyunuzu öğrenmek için ise, örneğin terzi mezurası kullanırsınız. Tersten; baskül boyunuzu söylemez, mezura da ağırlığınızı söylemez.
Ama, kim bilir, bakarsınız hızınıza bağlı örneğin koşarkenki dalgaboyunuzu ölçüp bildiriverecek telefon uygulamaları yakında piyasaya sürülüverir.
(*) Bkz., Principia.
Oysa, Newton’u önceleyen Galileo denklemlerinde mermilerin parabolik yörüngeler izlediği açıktı.
(**) Paul Langevin’in öğrencisi olarak 1908’de Fizik Doktorası almıştı.