Projects

Estimation of Time-Varying Graph Signals from Incomplete Observations (TUBITAK 1001 Project)

Many applications nowadays involve the acquisition of data over certain time intervals on platforms such as social networks, communication networks and irregular sensor arrays. Such data types can be modeled as time-varying graph signals. In many practical applications, it is not possible to observe graph signals as a complete data set with no missing samples; hence the need for estimating the unavailable observations of the graph signal using the available ones arises as an important need. Among many applications involving time-varying graph signals, some examples are the prediction of how an epidemic will evolve in a society, the estimation of lost data in a sensor network due to sensor failure or communication problems, the prediction of the tendencies of individuals in a social network such as their consumption habits. The purpose of this project is to develop novel methods for the modeling and estimation of time-varying graph signals.

Project Start Date: January 15, 2021

Project Duration: 30 months

 

Publications

  • E. T. Güneyi, B. Yaldız, A. Canbolat, and E. Vural, “Learning Graph ARMA Processes from Time-Vertex Spectra”, Submitted to IEEE Transactions on Signal Processing. [Online] Available: https://arxiv.org/abs/2302.06887

Abstract: The modeling of time-varying graph signals as stationary time-vertex stochastic processes permits the inference of missing signal values by efficiently employing the correlation patterns of the process across different graph nodes and time instants. In this study, we propose an algorithm for computing graph autoregressive moving average (graph ARMA) processes based on learning the joint time-vertex power spectral density of the process from its incomplete realizations for the task of signal interpolation. Our solution relies on first roughly estimating the joint spectrum of the process from partially observed realizations and then refining this estimate by projecting it onto the spectrum manifold of the graph ARMA process through convex relaxations. The initially missing signal values are then estimated based on the learnt model. Experimental results show that the proposed approach achieves high accuracy in time-vertex signal estimation problems.

  • A. Canbolat and E. Vural, “Locally Stationary Graph Processes”, Submitted to IEEE Transactions on Signal Processing. [Online] Available: https://arxiv.org/abs/2309.01657

Abstract: Stationary graph process models are commonly used in the analysis and inference of data sets collected on irregular network topologies. While most of the existing methods represent graph signals with a single stationary process model that is globally valid on the entire graph, in many practical problems, the characteristics of the process may be subject to local variations in different regions of the graph. In this work, we propose a locally stationary graph process (LSGP) model that aims to extend the classical concept of local stationarity to irregular graph domains. We characterize local stationarity by expressing the overall process as the combination of a set of component processes such that the extent to which the process adheres to each component varies smoothly over the graph. We propose an algorithm for computing LSGP models from realizations of the process, and also study the approximation of LSGPs locally with WSS processes. Experiments on signal interpolation problems show that the proposed process model provides accurate signal representations competitive with the state of the art. 

  • Canbolat and E. Vural, “Estimation of Locally Stationary Graph Processes from Incomplete Realizations”, IEEE International Workshop on Machine Learning for Signal Processing, 2022. 

Abstract: Stationarity is a well-studied concept in signal processing and the concept of stationary random processes has been extended to graph domains in several recent works. Meanwhile, in many scenarios a globally stationary process model may fail to accurately represent the correlation patterns of the data on the whole graph, e.g. when data is acquired on big graphs or when the behavior of the process varies significantly throughout the graph. In this work, we first propose a locally stationary graph process model, where the overall graph process is expressed through a combination of several local models. We then propose an algorithm that learns a locally stationary graph process model from partially observed realizations of the process. Experimental results show that the proposed locally stationary process model can provide significant gain in signal estimation performance compared to globally stationary models, even in cases where the process is highly stationary.

  • O. F. Kar, G. Turhan and E. Vural, “Learning Graph Signal Representations with Narrowband Spectral Kernels”, IEEE International Workshop on Machine Learning for Signal Processing, 2022.

Abstract: In this work, we study the problem of learning graph dictionary models from partially observed graph signals. We represent graph signals in terms of atoms generated by narrowband graph kernels. We formulate an optimization problem where the kernel parameters are learnt jointly with the signal representations under a triple regularization scheme: While the first regularization term aims to control the spectrum of the narrowband kernels, the second term encourages the reconstructed graph signals to vary smoothly on the graph, and the third term enforces that similar graph signals have similar representations over the learnt dictionaries. Once the graph kernels and signal representations are learnt, the initially unknown values of the signals are estimated based on the computed model. Experimental results show that the proposed method gives significant improvements in the estimation performance compared to reference approaches. 

  • A. B. Acar and E. Vural, “Learning Time-Vertex Dictionaries for Estimating Time-Varying Graph Signals”, IEEE International Workshop on Machine Learning for Signal Processing, 2022.

Abstract: In this work, we study the problem of learning time-vertex dictionaries for the modeling and estimation of time-varying graph signals. We consider a setting with a collection of partially observed time-varying graph signals, and propose a solution for the estimation of the missing signal observations by learning time-vertex dictionaries from the available observations. We adopt a time-vertex dictionary model defined through a set of joint time-vertex spectral kernels, each of which captures a different spectral component of the signals in their joint time-vertex spectrum. The kernel parameters are optimized along with the representations of the signals so as to be coherent with the available signal observations. Experimental results show that the proposed method yields promising estimation performance in comparison with non-adaptive graph dictionary models and baseline classical graph regression methods.

  • O. F. Kar, G. Turhan ve E. Vural, “Çizge Sinyallerinin Dar Bantlı Spektral Kernel Öğrenimi ile Kestirimi”, 30. IEEE Sinyal İşleme ve İletişim Uygulamaları Kurultayı, 2022.

Abstract: In this work, we study the problem of estimating graph signals from incomplete observations. We propose a method that learns the spectrum of the graph signal collection at hand by fitting a set of narrowband graph kernels to the observed signal values. The unobserved graph signal values are then estimated using the sparse representations of the signals in the graph dictionary formed by the learnt kernels. Experimental results on graph data sets show that the proposed method compares favorably to baseline graph-based semi-supervised regression solutions.

  • A. B. Acar ve E. Vural, “Zamanda Değişen Graf Sinyallerinin Kestirimi için Graflarda Sözlük Öğrenme”, 30. IEEE Sinyal İşleme ve İletişim Uygulamaları Kurultayı, 2022.

Abstract: We study the problem of estimating time-varying graph signals from missing observations. We propose a method based on learning graph dictionaries specified by a set of time-vertex kernels in the joint spectral domain. The parameters of the time-vertex kernels are optimized jointly with the sparse representation coefficients of the signals, so that the learnt representation fits well to the available observations of the time-vertex signals at hand. The missing observations of the signals are then estimated based on their reconstruction with the learnt model. Experimental results on real graph signal data sets show that the proposed method outperforms classical graph-based regression approaches.

  •  E. T. Güneyi, A. Canbolat and E. Vural, “Learning Parametric Time-Vertex Graph Processes from Incomplete Realizations,” 2021 IEEE 31st International Workshop on Machine Learning for Signal Processing (MLSP), 2021. (pdf)

Abstract: We consider the problem of estimating time-varying graph signals with missing observations, which is of interest in many applications involving data acquisition on irregular topologies. We model time-varying graph signals as jointly stationary time-vertex ARMA graph processes. We formulate the learning of ARMA process parameters as an optimization problem where the joint power spectral density of the model is fit to a rough empirical estimate of the process covariance matrix. We propose a convex relaxation of this problem, which results in an algorithm more flexible than existing methods regarding the pattern of available and missing observations of the process. Experimental results on meteorological signals show that the proposed method compares favorably to reference state-of-the-art algorithms.

An example realization of a time-varying graph signal modeled as a graph ARMA process. The illustration shows the values of the process taken at consecutive time instants.

  • G. Turhan and E. Vural, “Estimating Partially Observed Graph Signals by Learning Spectrally Concentrated Graph Kernels,” 2021 IEEE 31st International Workshop on Machine Learning for Signal Processing (MLSP), 2021. (pdf)

Abstract: Graph models provide flexible tools for the representation and analysis of signals defined over irregular domains such as social or sensor networks. However, in real applications data observations are often not available over the whole graph, due to practical problems such as sensor failure or connection loss. In this paper, we study the estimation of partially observed graph signals on multiple graphs. We learn a sparse representation of partially observed graph signals over spectrally concentrated graph dictionaries. Our dictionary model consists of several sub-dictionaries each of which is generated from a Gaussian kernel centered at a certain graph frequency in order to capture a particular spectral component of the graph signals at hand. The problem of jointly learning the spectral kernels and the sparse codes is solved with an alternating optimization approach. Finally, the incomplete entries of the given graph signals are estimated using the learnt dictionaries and the sparse coefficients. Experimental results on synthetic and real graph data sets suggest that the proposed method yields promising performance in comparison to reference solutions.

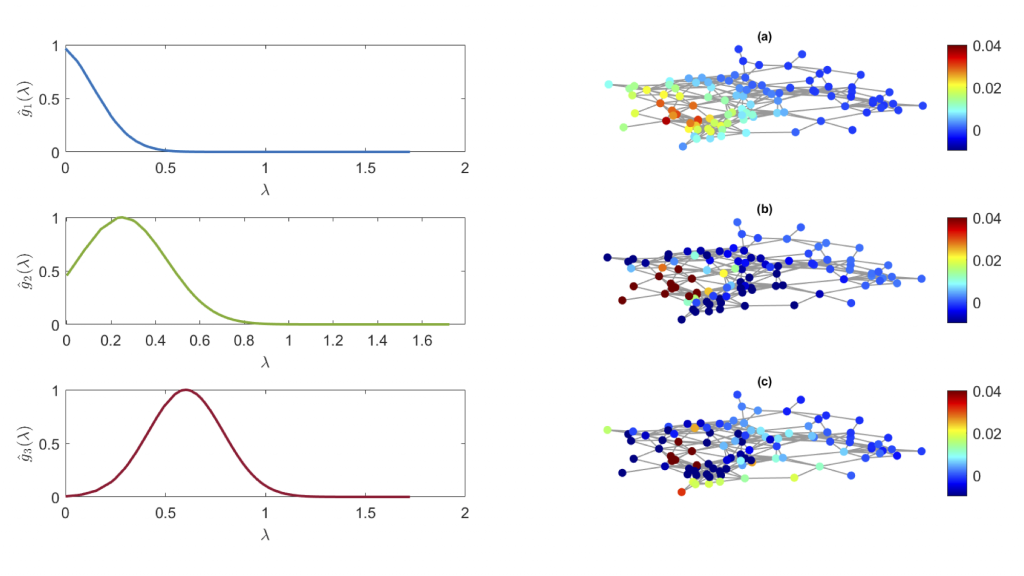
A low-pass Gaussian kernel and two different band-pass Gaussian kernels are shown together with the dictionary atoms they generate, localized at the same graph node. As the spectra of the atoms shift to high frequencies, their variation over the graph becomes more rapid.

Talks