Estimation of Time-Varying Graph Signals from Incomplete Observations
Many applications nowadays involve the acquisition of data over certain time intervals on platforms such as social networks, communication networks and irregular sensor arrays. Such data types can be modeled as time-varying graph signals. In many practical applications, it is not possible to observe graph signals as a complete data set with no missing samples; hence the need for estimating the unavailable observations of the graph signal using the available ones arises as an important need. Among many applications involving time-varying graph signals, some examples are the prediction of how an epidemic will evolve in a society, the estimation of lost data in a sensor network due to sensor failure or communication problems, the prediction of the tendencies of individuals in a social network such as their consumption habits. The purpose of this project is to develop novel methods for the modeling and estimation of time-varying graph signals. (View project page)
Domain Adaptation on Graphs
Most classification algorithms rely on the assumption that the labeled and unlabeled data samples at hand are drawn from the same distribution. However, in many practical data classification problems, the labeled training samples and the unlabeled test samples may have different statistics. Domain adaptation methods make use of the class labels sufficiently available in a source domain in order to infer the label information in a target domain where labeled data are much more scarce. In order to be able to “transfer” the information from one domain to another, some inherent relation must exist between the two domains.
We focus on settings where the source and the target data are represented with a graph in each domain. We consider that the source and the target graphs are related in such a way that the spectra of the source and the target class label functions on the two graphs share similar characteristics.
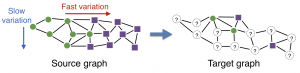
The idea in this work is to learn the spectrum of the label function in a source graph with many labeled nodes, and to transfer it to the spectrum of the target graph with fewer labeled nodes. A generic face manifold is illustrated in the figure below. Face images of three different individuals are indicated with different colors. While the class label function varies slowly along the blue direction, it has a relatively fast variation along the red direction.
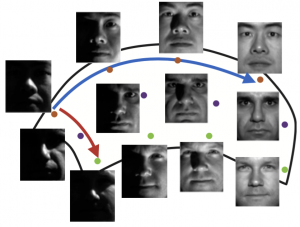
The graph domain adaptation problem we study is illustrated below. Given that the source label function has slow and fast variations along the indicated directions, the idea in our work is to transfer this label spectrum information to the target graph in order to estimate the target label function more accurately.
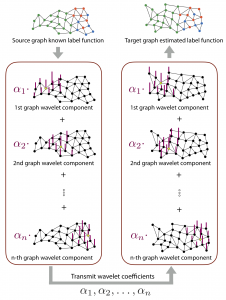
The transfer of information between two or more graphs can also be done in different ways, e.g. using localized bases for representing graph signals. In this study, we represent label functions in terms of Spectral Graph Wavelets (proposed by Hammond et al.) and transmit the wavelet coefficients of the label function between two graphs. This is illustrated in the figure below.
In order to get the best of graph domain adaptation methods, it is important to theoretically understand their performance limits. The classification performance significantly depends on the structures of the source and the target graphs and the similarity between them. In particular, in problems where the graphs are constructed from data samples coming from data manifolds, the properties of the graphs such as the locations and the weights of the edges, and the number of neighbors of graph nodes largely influence the performance of learning.
In this work, we propose a theoretical characterization of the performance of classification on the target graph in a graph domain adaptation setting. Our theoretical analysis suggests that very sparse graphs with too few edges and very dense graphs with too many edges should be avoided, as well as too small edge weights. The smoothness of the label function is shown to positively influence the performance of learning. We then use these theoretical findings to propose a graph domain adaptation algorithm that jointly estimates the class labels of the source and the target data and the topologies of the source and the target graphs.
Dimensionality Reduction
Traditional algorithms such as PCA and LDA learn a linear projection that reduces the dimensionality of data while capturing its main and discriminative properties. During the last two decades, many studies have aimed to take into account the nonlinear but low-dimensional intrinsic structure of data in order to learn efficient models and classifiers, which are called manifold learning methods. Supervised manifold learning methods learn a mapping for better separability of different classes, as illustrated below.
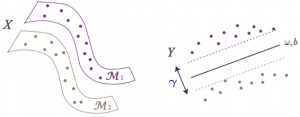
Supervised manifold-learning methods often focus on learning an embedding for the training data that achieves favourable separation between different classes. However, the extension of these embeddings for initially unavailable samples and the generalization performance of these embeddings to new data samples have rather been overlooked. We address these problems by proposing generalization bounds for supervised manifold learning algorithms and semi-supervised out-of-sample extensions.
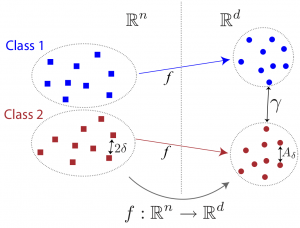
Our generalization bounds show that for successfully generalizing the learnt embedding to new samples, the Lipschitz regularity of the interpolation function f should be made sufficiently small, taking into account the separation between different classes and the preservation of the local geometry (illustrated in the figure below). These theoretical results can then be used for improving the performance of supervised manifold learning algorithms. Motivated by these theoretical findings, we propose in this study a supervised manifold learning method that computes a nonlinear embedding while constructing a smooth and regular interpolation function that extends the embedding to the whole data space in order to achieve satisfactory generalization. The embedding and the interpolator are jointly learnt such that the Lipschitz regularity of the interpolator is imposed while ensuring the separation between different classes.
Multi-modal Learning
With the increasing accessibility of data acquisition and storing technologies, the need for successfully analyzing and interpreting multi-modal data collections has become more important. Many applications involve the acquirement or analysis of data collections available in multiple modalities. In this work, we have studied the problem of learning supervised nonlinear representations for multi-modal classification and cross-modal retrieval applications.
We have first theoretically analyzed the learning of multi-modal nonlinear embeddings in a supervised setting. The studied multi-modal embedding setting is illustrated below. In this example, modalities u (image) and v (text) are mapped to the common domain via interpolators f(u) and f(v). The parameters η, Rδ, and γ respectively measure the alignment between different modalities, the within-class compactness, and the separation between different classes. (Images: wikipedia.org)
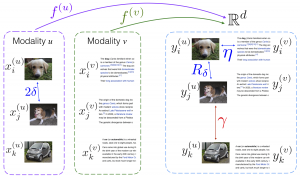
Our performance bounds indicate that for successful generalization in multi- modal classification and retrieval problems, the regularity of the interpolation functions extending the embedding to the whole data space is as important as the between-class separation and cross-modal alignment criteria. We have then used these results to propose a multi-modal nonlinear representation learning algorithm, where the embeddings of the training samples are optimized jointly with the Lipschitz regularity of the interpolators.