4.2 Mekanizmalarda Hız ve İvme Analizi -2

Örnek:

Cismin A ve B noktalarının hızları şekilde gösterildiği gibidir. S noktasının hız vektörünü bulun.

v_A ve v_B hız vektörleri o_v başlangıç noktasından çizildiğinde uçları a ve b noktaları olarak işaretlenecektir. Hız poligonunda oluşacak olan abs üçgeni ile cisim üzerinde mevcut ABS üçgenlerinin benzer yapacak şekilde oluşturulması gerekmektedir. Benzer üçgenlerin açıları aynıdır. Bu nedenle b noktasından xb doğrusunu ∠xba = ∠SBA olacak şekilde ve a noktasından ua doğrusunu ∠uab = ∠SAB olacak şekilde çizdiğimizde ua ve xb doğrularının kesim noktası s dir ve o_v s vektörü S noktasının v_S hız vektörüdür (Şekil b).

Örnek:

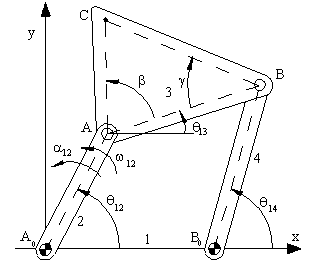
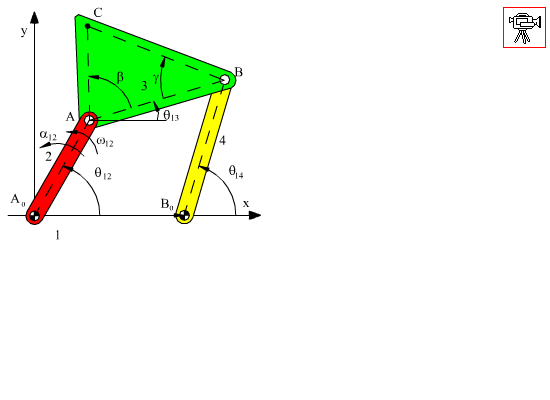
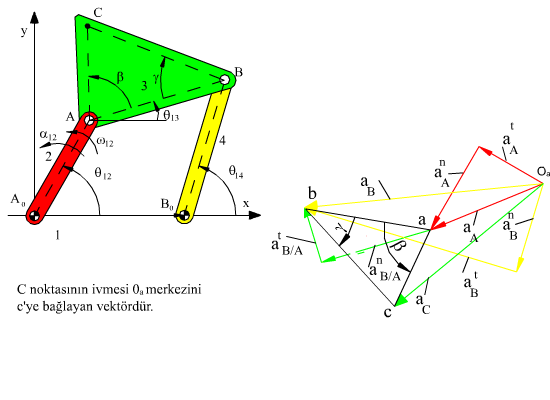
Şekilde gösterilen bir dört-çubuk mekanizmasında |A₀B₀| = a₁, |A₀A| = a₂, |AB| = a₃, |AC| = b₃, |B₀B| = a₄. Hız ve ivme analizini yapalım. Devre kapalılık denklemi ve eşleniği:

a₂e^iθ₁₂ + a₃e^iθ₁₃ = a₁ + a₄e^iθ₁₄

a₂e^−iθ₁₂ + a₃e^−iθ₁₃ = a₁ + a₄e^-iθ₁₄

Devre kapalılık denkleminin birinci türevi alındığında elde edilen hız devre denklemi:

ia₂ω₁₂e^iθ₁₂ + ia₃ω₁₃e^iθ₁₃ = ia₄ω₁₄e^iθ₁₄

−ia₂ω₁₂e^−iθ₁₂ − ia₃ω₁₃e^−iθ₁₃ = −ia₄ω₁₄e^−iθ₁₄

elde edilecektir. Dikkat edilir ise, hız devre denklemi vektörel olarak:

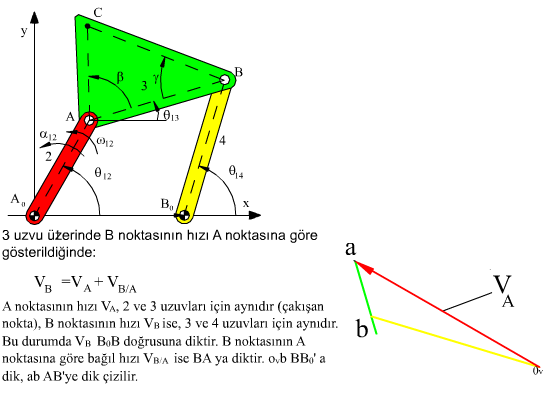
v_A + v_B/A = v_B

denklemidir. Karmaşık sayılarla yazılmış olan her bir hız teriminin tanımı genellikle kolayca yapılabilir ve mutlaka bağıl hız kavramı ile elde edilecek vektör eşitlik denklemi ile aynı sonuç vermesi gereklidir. Bir başka anlatımla, karmaşık sayılar ile yazılan hız devre denklemleri, vektörel hız denklemlerinin farklı bir yazılış şeklidir. Vektörel hız denklemleri analitik veya geometrik yöntemle çözülebilir. Analitik olarak karmaşık sayılar ile yazılmış olan hız devre denklemlerinin bilinmeyen hız denklemlerine göre çözümü genellikle daha basit sonuç vermektedir. Denklemler verilen giriş hızı ω₁₂ ile bilinmeyen ω₁₃ ve ω₁₄ açısal hız değişkenlerine göre lineer olup eğer konum analizi önceden yapılmış ve verilen θ₁₂ açısına göre θ₁₃ ile θ₁₄ açılarının o konumda aldığı değerler bulunmuş ise ω₁₃ ve ω₁₄ hız değişkenlerine Cramer kuralı kullanılarak çözüm yapılabilir:

\displaystyle {{\text{ω}}_{{13}}}=\frac{{\left| {\begin{array}{cc} {-{{\text{a}}_{2}}{{\text{ω}}_{{12}}}{{\text{e}}^{{\text{i}{{\text{θ}}_{{12}}}}}}} & {-{{\text{a}}_{4}}{{\text{e}}^{{\text{i}{{\text{θ}}_{{14}}}}}}} \\ {-{{\text{a}}_{2}}{{\text{ω}}_{{12}}}{{\text{e}}^{{-\text{i}{{\text{θ}}_{{12}}}}}}} & {-{{\text{a}}_{4}}{{\text{e}}^{{-\text{i}{{\text{θ}}_{{14}}}}}}} \end{array}} \right|}}{{\left| {\begin{array}{cc} {{{\text{a}}_{3}}{{\text{e}}^{{\text{i}{{\text{θ}}_{{13}}}}}}} & {-{{\text{a}}_{4}}{{\text{e}}^{{\text{i}{{\text{θ}}_{{14}}}}}}} \\ {{{\text{a}}_{3}}{{\text{e}}^{{-\text{i}{{\text{θ}}_{{13}}}}}}} & {-{{\text{a}}_{4}}{{\text{e}}^{{-\text{i}{{\text{θ}}_{{14}}}}}}} \end{array}} \right|}}=\frac{{{{\text{a}}_{2}}{{\text{a}}_{4}}\left( {{{\text{e}}^{{\text{i}\left( {{{\text{θ}}_{{12}}}-{{\text{θ}}_{{14}}}} \right)}}}-{{\text{e}}^{{-\text{i}\left( {{{\text{θ}}_{{12}}}-{{\text{θ}}_{{14}}}} \right)}}}} \right)}}{{{{\text{a}}_{3}}{{\text{a}}_{4}}\left( {-{{\text{e}}^{{-\text{i}\left( {{{\text{θ}}_{{14}}}-{{\text{θ}}_{{13}}}} \right)}}}+{{\text{e}}^{{\text{i}\left( {{{\text{θ}}_{{14}}}-{{\text{θ}}_{{13}}}} \right)}}}} \right)}}{{\text{ω}}_{{12}}}=\frac{{{{\text{a}}_{2}}}}{{{{\text{a}}_{3}}}}\frac{{\sin \left( {{{\text{θ}}_{{12}}}-{{\text{θ}}_{{14}}}} \right)}}{{\sin \left( {{{\text{θ}}_{{14}}}-{{\text{θ}}_{{13}}}} \right)}}{{\text{ω}}_{{12}}}

Benzer bir şekilde:

\displaystyle {{\text{ω}}_{{14}}}=\frac{{\left| {\begin{array}{cc} {{{\text{a}}_{3}}{{\text{e}}^{{\text{i}{{\text{θ}}_{{13}}}}}}} & {-{{\text{a}}_{2}}{{\text{ω}}_{{12}}}{{\text{e}}^{{\text{i}{{\text{θ}}_{{12}}}}}}} \\ {{{\text{a}}_{3}}{{\text{e}}^{{-\text{i}{{\text{θ}}_{{13}}}}}}} & {-{{\text{a}}_{2}}{{\text{ω}}_{{12}}}{{\text{e}}^{{-\text{i}{{\text{θ}}_{{12}}}}}}} \end{array}} \right|}}{{\left| {\begin{array}{cc} {{{\text{a}}_{3}}{{\text{e}}^{{\text{i}{{\text{θ}}_{{13}}}}}}} & {-{{\text{a}}_{4}}{{\text{e}}^{{\text{i}{{\text{θ}}_{{14}}}}}}} \\ {{{\text{a}}_{3}}{{\text{e}}^{{-\text{i}{{\text{θ}}_{{13}}}}}}} & {-{{\text{a}}_{4}}{{\text{e}}^{{-\text{i}{{\text{θ}}_{{14}}}}}}} \end{array}} \right|}}=\frac{{{{\text{a}}_{3}}{{\text{a}}_{2}}\left( {-{{\text{e}}^{{-\text{i}\left( {{{\text{θ}}_{{12}}}-{{\text{θ}}_{{13}}}} \right)}}}+{{\text{e}}^{{\text{i}\left( {{{\text{θ}}_{{12}}}-{{\text{θ}}_{{13}}}} \right)}}}} \right)}}{{{{\text{a}}_{3}}{{\text{a}}_{4}}\left( {-{{\text{e}}^{{-\text{i}\left( {{{\text{θ}}_{{14}}}-{{\text{θ}}_{{13}}}} \right)}}}+{{\text{e}}^{{-\text{i}\left( {{{\text{θ}}_{{14}}}-{{\text{θ}}_{{13}}}} \right)}}}} \right)}}{{\text{ω}}_{{12}}}=\frac{{{{\text{a}}_{2}}}}{{{{\text{a}}_{4}}}}\frac{{\sin \left( {{{\text{θ}}_{{12}}}-{{\text{θ}}_{{13}}}} \right)}}{{\sin \left( {{{\text{θ}}_{{14}}}-{{\text{θ}}_{{13}}}} \right)}}{{\text{ω}}_{{12}}}

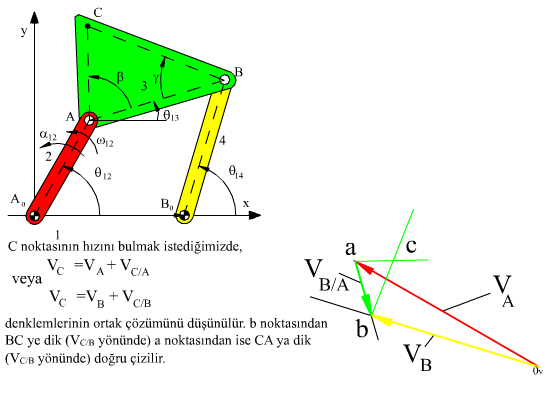
C noktasının hızı isteniyor ise, C nin konum vektörü:

r_C = a₂e^iθ₁₂ + b₃e^{i(θ₁₃ + β)}

r_C konum vektörünün zamana göre türevi, C noktasının hız vektörünü tanımlar:

v_C = \displaystyle {\dot{\text{x}}} _C + i \displaystyle {\dot{\text{y}}} _C = ia₂ω₁₂e^iθ₁₂ + ib₃ω₁₃e^{i(θ₁₃ + β)}

Bu denklem

v_C = v_A + v_C/A

vektörel hız denklemidir. x ve y bileşenleri:

\displaystyle {\dot{\text{x}}} _C = −ia₂ω₁₂sinθ₁₂ − ib₃ω₁₃sin(θ₁₃ + β)

\displaystyle {\dot{\text{y}}} _C = a₂ω₁₂cosθ₁₂ + b₃ω₁₃cos(θ₁₃ + β)

dır. Eğer devre kapalılık denklemi ve hız devre denklemleri önceden çözülmüş ise, yukarıda verilmiş olan denklemlerin sağ tarafında kalan terimlerin tümü bilinmektedir. Hızın x ve y bileşenleri çözüldükten sonra istenildiğinde kutupsal koordinat sistemi kullanılarak hız bir şiddet ve yön açısı ile gösterilebilir. Bu durumda C noktasının hız vektörü karmaşık sayı ile

v_C = v_Ce^iη

dır. Bu denklemde v_C = \displaystyle \sqrt{{{{{\dot{\text{x}}}}_{\text{C}}}^{2}+{{{\dot{\text{y}}}}_{\text{C}}}^{2}}} hız şiddeti ve η = tan^-1( \displaystyle {\dot{\text{y}}} _C/ \displaystyle {\dot{\text{x}}} _C) hız vektörünün pozitif x eksenine göre yaptığı açıdır.

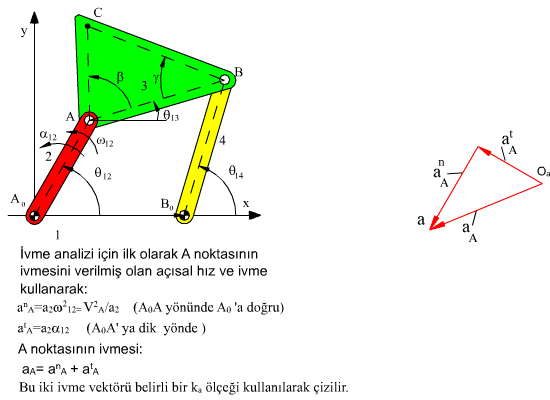
İvme analizi için karmaşık sayı ile yazılmış olan hız devre denkleminin türevi alınarak ivme devre denklemi elde edilecektir:

ia₂α₁₂e^iθ₁₂ − a₂ω₁₂²e^iθ₁₂ + ia₃α₁₃e^iθ₁₃ − a₃ω₁₃²e^iθ₁₃ = ia₄α₁₄e^iθ₁₄ − a₄ω₁₄²e^iθ₁₄

−ia₂α₁₂e^−iθ₁₂ − a₂ω₁₂²e^−iθ₁₂ − ia₃α₁₃e^−iθ₁₃ − a₃ω₁₃²e^−iθ₁₃ = −ia₄α₁₄e^−iθ₁₄ − a₄ω₁₄²e^−iθ₁₄

Dikkat edilir ise yazılmış olan hız devre denklemi vektörel olarak:

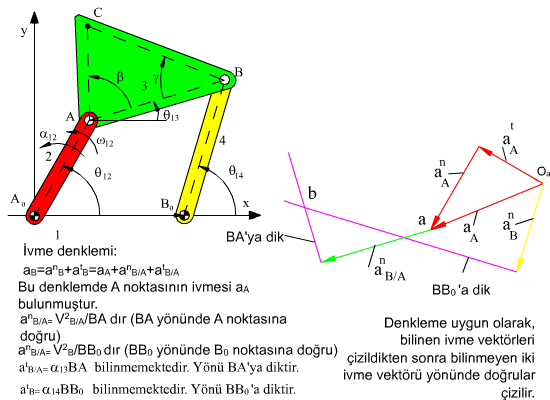
a^t_A + aⁿ_A + a^t_B/A + aⁿ_B/A = a^t_B + aⁿ_B

denkleminden farklı değildir. İvme devre denkleminde bilinen terimleri denklemin sağ tarafında kümeler isek:

  ia₃α₁₃e^iθ₁₃ − ia₄α₁₄e^iθ₁₄ = −ia₂α₁₂e^iθ₁₂ + a₂ω₁₂²e^iθ₁₂ + a₃ω₁₃²e^iθ₁₃ − a₄ω₁₄²e^iθ₁₄

−ia₃α₁₃e^−iθ₁₃ + ia₄α₁₄e^−iθ₁₄ = ia₂α₁₂e^−iθ₁₂ + a₂ω₁₂²e^−iθ₁₂ + a₃ω₁₃²e^−iθ₁₃ − a₄ω₁₄²e^−iθ₁₄

Denklemi bilinmeyen ivme değişkenleri α₁₃ ve α₁₄ için çözdüğümüzde:

α₁₃ = \displaystyle \frac{{{{\text{a}}_{2}}{{\text{α}}_{{12}}}\sin \left( {{{\text{θ}}_{{12}}}-{{\text{θ}}_{{14}}}} \right)+{{\text{a}}_{2}}{{\text{ω}}_{{12}}}^{2}\cos \left( {{{\text{θ}}_{{12}}}-{{\text{θ}}_{{14}}}} \right)-{{\text{a}}_{4}}{{\text{ω}}_{{12}}}^{2}+{{\text{a}}_{3}}{{\text{ω}}_{{13}}}^{2}\cos \left( {{{\text{θ}}_{{14}}}-{{\text{θ}}_{{13}}}} \right)}}{{{{\text{a}}_{3}}\sin \left( {{{\text{θ}}_{{14}}}-{{\text{θ}}_{{13}}}} \right)}}

ve

α₁₄ = \displaystyle \frac{{{{\text{a}}_{2}}{{\text{α}}_{{12}}}\sin \left( {{{\text{θ}}_{{12}}}-{{\text{θ}}_{{13}}}} \right)+{{\text{a}}_{2}}{{\text{ω}}_{{12}}}^{2}\cos \left( {{{\text{θ}}_{{12}}}-{{\text{θ}}_{{13}}}} \right)-{{\text{a}}_{3}}{{\text{ω}}_{{12}}}^{2}\cos \left( {{{\text{θ}}_{{14}}}-{{\text{θ}}_{{13}}}} \right)+{{\text{a}}_{3}}{{\text{ω}}_{{13}}}^{2}}}{{{{\text{a}}_{4}}\sin \left( {{{\text{θ}}_{{14}}}-{{\text{θ}}_{{13}}}} \right)}}

C noktasının ivmesi ise C noktasının hız vektörünün zamana göre türevi alınarak elde edilir.

a_C = ia₂α₁₂e^iθ₁₂ − a₂ω₁₂²e^iθ₁₂ + ib₃α₁₃e^{i(θ₁₃ + β)} − b₃ω₁₃²e^{i(θ₁₃ + β)}

Dikkat edilir ise, devre kapalılık denklemi, hız ve ivme devre denklemleri çözülmüş ise, sağ tarafta bulunan terimler bilinen değerlerdir. Bu denklem vektörel olarak

a_C = aⁿ_A + a^t_A + aⁿ_C/A + a^t_C/A

denklemi ile aynıdır. Görüldüğü gibi devre kapalılık denklemi ve türevleri olan hız ve ivme denklemleri çözüldükten sonra mekanizmada bulunan her hangi bir uzvun üzerinde bir noktanın konumu, hızı ve ivmesi kolaylıkla belirlenebilir.

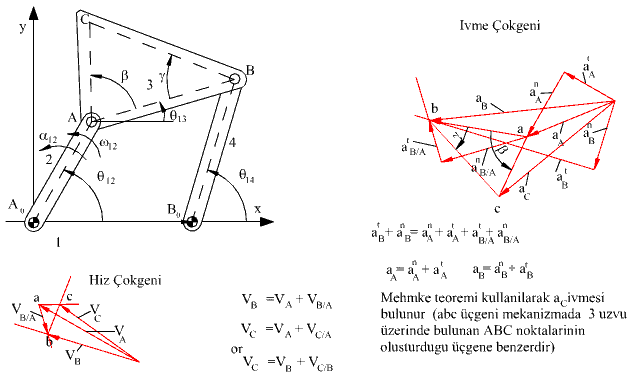
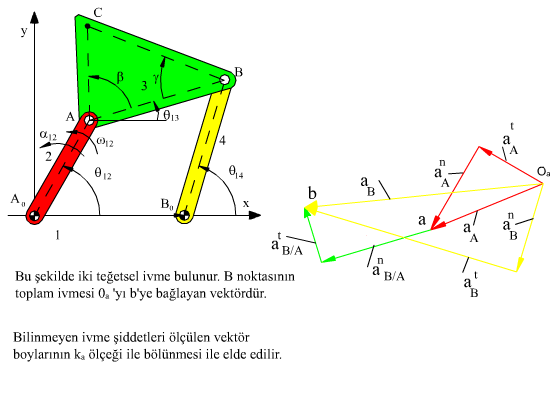
Yukarıda ki şekilde dört-çubuk mekanizması için hız ve ivme analizinin grafik çözümü gösterilmiştir.

Hız ve ivme analizini kademe kademe incelemek için aşağıda verilen flash animasyonunu kullanabilirsiniz.

Yukarıda gösterilmiş olan şeklin Autocad kütüğü için tıklayınız: –DortCubuk.dwg–

Hız ve ivme devre denklemleri daima hız ve ivme değişkenlerine göre lineerdir. Devre kapalılık denklemleri, konum değişkenlerine göre lineer olmadıklarından dolayı, çözümü lineer denklem çözümüne göre belirli zorluk gösterir (veya deneme-yanılma gerektiren bir çözüm gerekebilir).

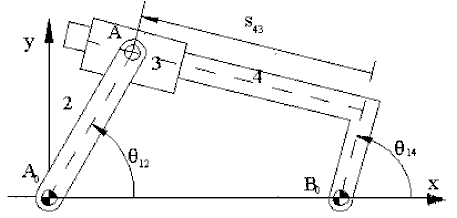
Yukarıda gösterilen kol-kızak mekanizmasında |A₀B₀| = a₁, |A₀A| = a₂, |B₀B| = a₄ (ofset). Devre kapalılık denklemi:

a₂e^iθ₁₂ = a₁ + a₄e^iθ₁₄ + is₄₃e^iθ₁₄

olacaktır. Zamana göre türevi alındığında hız devre denklemi:

iω₁₂a₂e^iθ₁₂ = iω₁₄a₄e^iθ₁₄ − ω₁₄s₄₃e^iθ₁₄ + i \displaystyle {\dot{\text{s}}}₄₃e^iθ₁₄

Terimler tekrar gruplandırıldığında:

iω₁₂a₂e^iθ₁₂ = iω₁₄(a₄ + is₄₃)e^iθ₁₄ + i \displaystyle {\dot{\text{s}}}₄₃e^iθ₁₄

Bu hız devre denklemi hız vektörleri ile yazıldığında:

v_A2 = v_A3 = v_A4 + v_A3/A4

Hız denkleminde solda görülen birinci terim 2 uzvu üzerinde bulunan A₂ noktasının hızıdır. Bu hızın şiddeti, noktanın merkezden uzaklığı (|A₀A| = a₂) ile 2 uzvunun açısal hızının (ω₁₂) çarpımıdır. A₂ ve A₃ noktaları daima çakışan noktalar olduğundan, konumları ve hızları aynı olacaktır. Denklemin sağında bulunan birinci terim ise 4 uzvu üzerinde bulunan A₄ noktasının hızıdır. Bu hızın şiddeti bu noktanın dönme merkezinden uzaklığının (|B₀B| = a₄), 4 uzvunun açısal hızı ile (ω₁₄) çarpımıdır. İkinci terim ise A₃ noktasının 4 uzvuna göre yaptığı bağıl hızdır. Bu hızın yönü 3 ve 4 uzuvları arasında bulunan kayar çift eksenine paraleldir.

İvme devre denklemi hız devre denkleminin zamana göre türevi ile elde edilir:

iα₁₂a₂e^iθ₁₂ − ω₁₂²a₂e^iθ₁₂ = iα₁₄(a₄ + is₄₃)e^iθ₁₄ − iω₁₄²(a₄ + is₄₃)e^iθ₁₄ + i \displaystyle {\ddot{\text{s}}}₄₃e^iθ₁₄ − 2 \displaystyle {\dot{\text{s}}}₄₃ω₁₄e^iθ₁₄

Dikkat edildiğinde bu denklem vektörel olarak

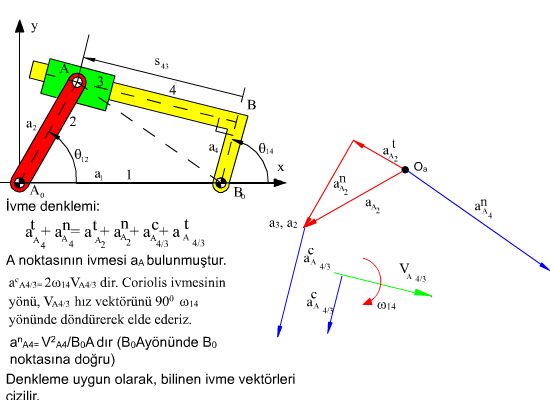
a^t_A2 + aⁿ_A2 = a^t_A3 + aⁿ_A3 = a^t_A4 + aⁿ_A4 + a^t_A3/A4 + a^c_A3/A4

olur. A₂ ve A₃ noktalarının ivmeleri birbirlerine eşittir. Normal ivme aⁿ_A2 şiddeti iki uzvunun açısal hızının karesi ile noktanın dönme merkezine uzaklığı ile çarpımı, yönü ise o noktadan dönme merkezine doğrudur. Teğetsel ivme a^t_A2 ise noktanın merkeze uzaklığı ile açısal ivmenin çarpımı, yönü ise noktayı merkeze bağlayan doğruya diktir. Benzer bir şekilde A₄ noktasının normal ve teğetsel ivmeleri sırası ile AB₀ yönünde veya B₀A ya dik yöndedir. Üçüncü terim ise bağıl teğetsel ivme olup 3 ve 4 uzuvları arsındaki kayar çift eksenine paralel yöndedir. Şiddeti ise \displaystyle {\ddot{s}}₄₃ dür. Son terim ise Coriolis ivmesi olup şiddeti bağıl hız ile 4 uzvunun açısal hızının çarpımının iki katı olup (2 \displaystyle {\dot{s}}₄₃ω₁₄) yönü kayar mafsal eksenine diktir.

Aşağıda verilmiş olan şeklin AutoCad kütüğü için tıklayınız: –KolKızak.dwg–

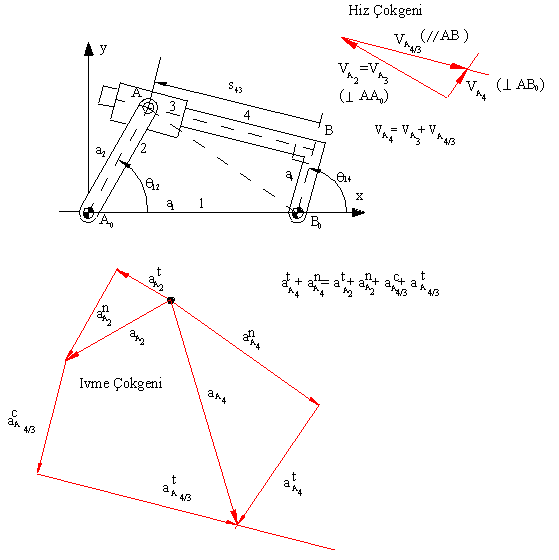
Yukarıda gösterilen şekilde grafik olarak hız ve ivme poligonları görülmektedir. Dikkat edilir ise çizilen hız poligonu:

v_A4 = v_A3 + v_A4/A3

denklemi ile uyumludur (denklemin her bir tarafında bir bilinmeyen kalması için). v_A3 = v_A2 dir ve bu vektörün şiddeti ω₁₂|AA₀| dır. ω₁₂ bilinen açısal hız ise, vektörün şiddeti ve yönü (A₀A ya dik) bilinmektedir. v_A4 hızı, AB₀‘a diktir. v_A4/A3 bağıl hız vektörü ise kayar mafsal eksenine paralel olacaktır. İlk olarak v_A3 belirli bir ölçek ile çizilir. Daha sonra bu vektörün uç noktasından kayar mafsal eksenine paralel v_A4/A3 yönünde bir doğru, başlangıç noktasından ise AB₀‘a dik v_A4 yönünde doğru çizilir. Bu doğruların kesiştiği nokta bu iki vektörün uç noktasıdır. v_A4 ve v_A4/A3 hız vektörlerinin şiddeti, bulunan uzunlukların v_A2 hız vektörünü çizerken kullanılan ölçek ile bölünmesi ile bulunur. v_A4 hız vektörünün bulunması ile şiddetinin AB₀‘a bölünmesi ile ω₁₃ = ω₁₄ açısal hızı da bulunabilir (3 ve 4 uzuvları arasında kayar mafsal olduğundan bu iki uzuv aynı miktarda açısal dönme yapabilirler ve açısal hız ve ivmeleri aynı olmalıdır). v_A4 hız vektörünün yönüne göre, ω₁₄ hız vektörü saat yelkovanı yönünde olmalıdır.

İvme analizi için ivme devre denklemi :

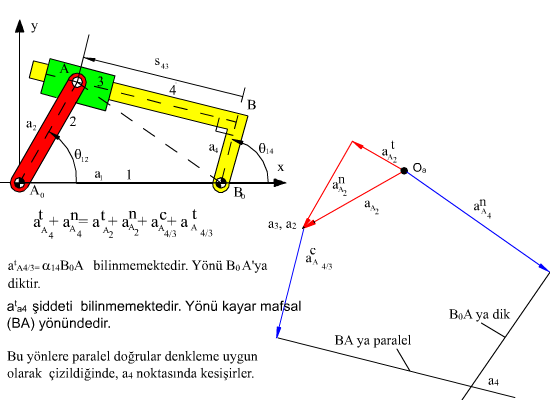
a^t_A4 + aⁿ_A4 = a^t_A3 + aⁿ_A3 + a^c_A4/A3 + a^t_A4/A3

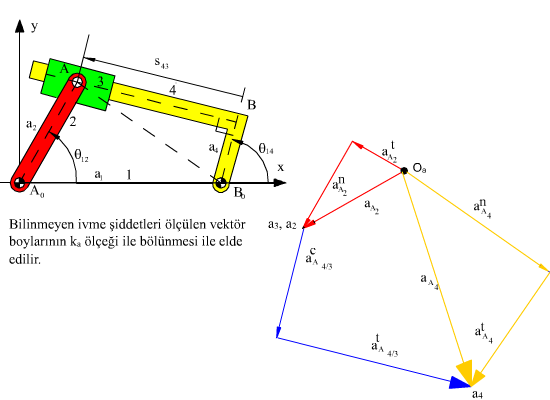
olarak yazılabilir. Bu değişik yazımın tek nedeni denklemin her iki tarafında bir bilinmeyen bırakmak içindir. Grafik ivme analizine bilinen ivme vektörlerinin belirli bir ölçek ile çizilmesi ile başlanılır. Örneğin a^t_A3 = a^t_A2 nin şiddeti α₁₂|AA₀| ve yönü AA₀‘a dik olacaktır ve aⁿ_A3 = aⁿ_A2 nin şiddeti ω₁₂²|AA₀| olup, yönü AA₀ yönünde A₀‘a doğru olacaktır. Her iki ivme vektörü istenilen sırada uc uca çizilir. İki ivme vektörünün toplamı A₂ veya A₃ noktasının toplam ivmesidir (a_A3 = a_A2). Bundan sonra Coriolis ivme bileşkesinin şiddeti 2ω₁₄ \displaystyle {\dot{s}}₄₃ olarak bulunur. Bu terimde bulunan bağıl hız ve açısal hız değerleri hız analizi yapıldı ise bilinmektedir. Coriolis ivmesinin yönünü belirlemek için bağıl hız vektörü göz önüne alınır ve bu vektörün 90⁰ açısal hız yönünde döndürülmesi bize Coriolis ivmesinin yönünü gösterir. Yönü ve şiddeti bulunan coriolis ivmesi a^c_A4/A3, a_A2 ivme vektörünün uç noktasından, kullanılan aynı ölçek ile çizilir. Bu yönde son olarak şiddeti bilinmeyen ancak yönü kayar mafsal eksenine paralel olması gereken a^t_A4/A3 ivme vektörünün yönünü belirleyen kayar çift eksenine paralel doğru, coriolis ivme vektörünün ucundan çizilir. Denklemin sağ tarafında bulunan terimleri ele aldığımızda A₄ noktasının normal ivmesi aⁿ_A4 ün şiddeti ω₁₃²|AB₀| (veya v_A4²/|AB₀|) olduğu ve yönünün ise AB₀ yönünde ve dönme merkezi B₀ a doğru olduğu görülür. Dikkat edilir ise ivme denkleminde bulunan tüm normal ivme ve Coriolis ivme terimleri hız analizine bağlıdır ve hız analizi yapıldı ise gerek şiddetleri ve gerek yönleri bilinmektedir. a_A2 ivme vektörünün başlangıç noktasından ilk olarak diğer vektörler için kullanılmış olan ölçek kullanılarak aⁿ_A4 ivmesi çizilir. A₄ noktasının teğetsel ivmesi, a^t_A4 vektörünün şiddeti bilinmemetedir ancak yönü, 4 uzvu dönme yaptığından AB₀ doğrusuna dik olmalıdır. Öyle ise normal ivmenin uç noktasından AB₀‘a dik doğru çizilir. Bu doğru ile bağıl teğetsel ivme yönü için çizmiş olduğumuz kayar mafsal eksenine paralel doğrunun kesim noktası ivme poligonunun çözümüdür.

Hız ve ivme analizini kademe kademe incelemek için aşağıda verilen animasyonu inceleyiniz.

Verilmiş olan AutoCad Çizim kütüğünü kullanarak:

a) Hangi hız ve ivme teriminin mekanizmada neye paralel veya dik olduğunu belirleyin.

b) Sabit giriş kolu açısal hızı ω₁₂ = 1 rad/s için hız ve ivme değerlerinin boyutlarını belirleyin.

Bundan sonraki iki bölümde verilmiş olan örneklerde bazı düzlemsel mekanizmaların konum hız ve ivme analizleri grafik veya analitik olarak yapılmıştır.