Design of Drag-link Mechanisms with optimum transmission angle
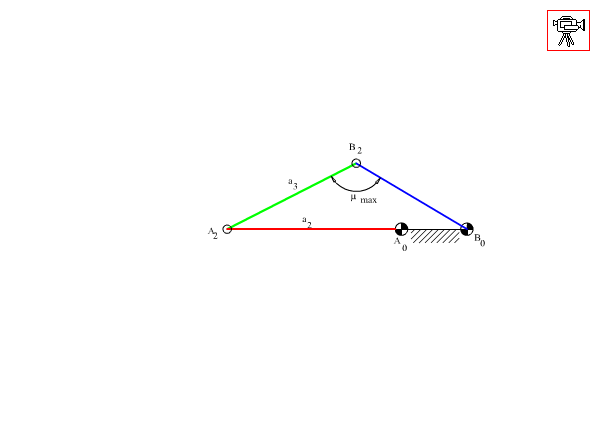
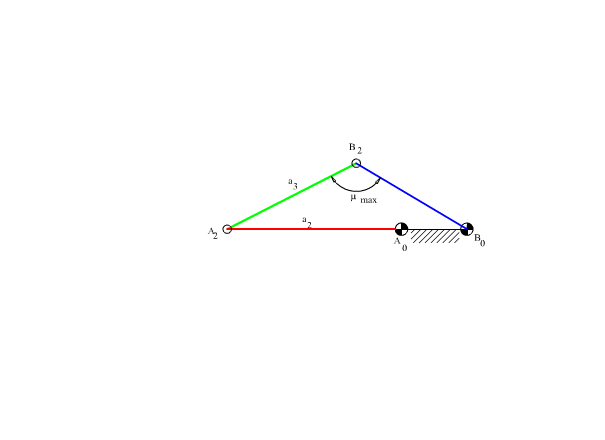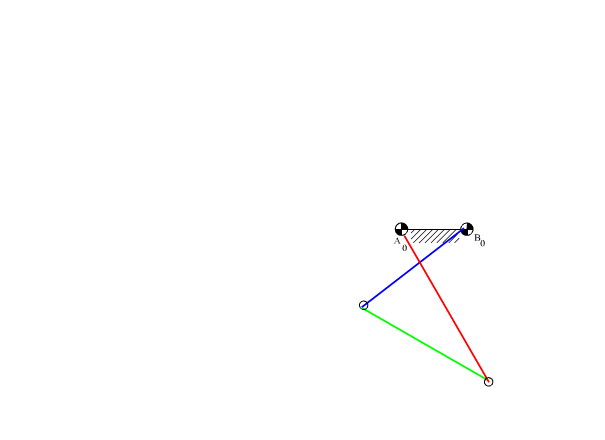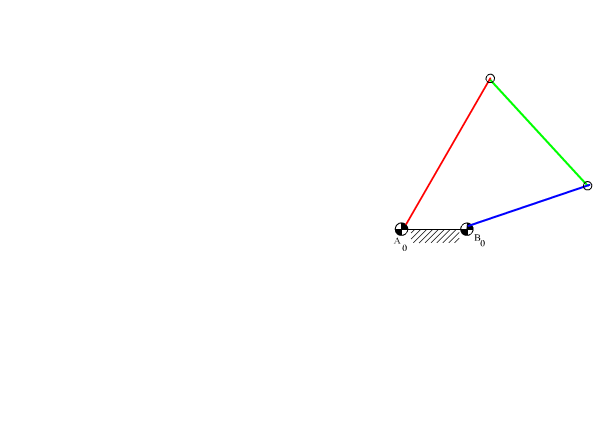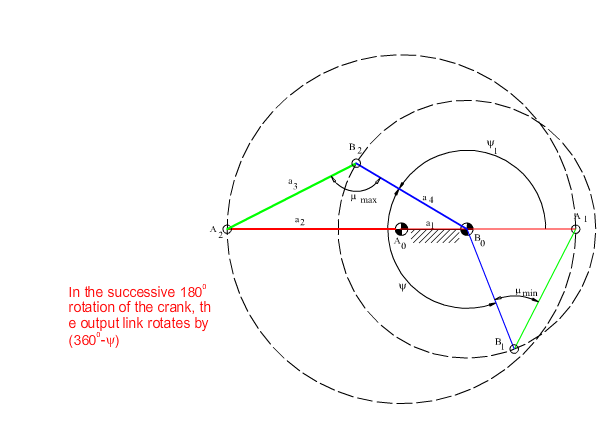
Drag-link mechanisms are used to convert a uniform continuous rotation into a nonuniform continuous rotary motion. They can be used in series with crank-rocker mechanism to obtain a different motion characteristics. In figure below the four-bar mechanism with drag-link proportions is shown in positions where the deviation of the transmission angle from 900 is maximum (the input crank and the fixed link are collinear). It develops that the transmission angle is optimum when the two maximum deviations are equal (mmax-900=900–mmin).
Corresponding to 1800 input crank rotation, the output link will be required to rotate by y (Note that y <1800, since the output link will rotate 3600–y for the next 1800 rotation of the crank). Let us also assume a minimum value of the transmission angle mmin. The two extreme positions will be as shown in Fig. 7.16. For the best transmission angle characteristics, at these two extreme positions if we equate the transmission angle deviations, we obtain the loop equations as:
| −a1 − a2 + a3ei(ψ1 − π + μmin) = a4eiψ1 | (1) |
| −a1 + a2 + a3ei(ψ1 + ψ − μmin) = a4ei(ψ1 + ψ) | (2) |
In addition, in order to obtain equal transmission angle deviations at the two extreme positions:
| a12 + a22 = a32 + a42 | (3) |
using a1 =1 (scaling) , λ = a4/a3 and letting Z = a3eiψ1, equations (1) and (2) can be written as:
| −1 − a2 − Zeiμmin = λZ | (4) |
| −1 + a2 + Zei(ψ − μmin) = λZeiψ | (5) |
Eliminating Z from equations (4) and (5):
| \displaystyle \frac{{1+{{\text{a}}_{2}}}}{{1-{{\text{a}}_{2}}}}=\frac{{\text{λ}+{{\text{e}}^{{\text{i}{{\text{μ}}_{{\text{min}}}}}}}}}{{{{\text{e}}^{{\text{iψ}}}}\left( {\text{λ}-{{\text{e}}^{{\text{i}{{\text{μ}}_{{\text{min}}}}}}}} \right)}} | (6) |
Which can be put into the form:
| a2[λcos(ψ/2) − i sin(ψ/2 − μmin)] + i λsin(ψ/2) − cos(ψ/2 − μmin) = 0 | (7) |

Equating the real and imaginary parts to zero and solving for l and a2 yields:
| \displaystyle {{\text{λ}}^{2}}=\frac{{\sin \left( {\text{ψ}-2{{\text{μ}}_{{\text{min}}}}} \right)}}{{\sin \left( \text{ψ} \right)}} | (8) |
| \displaystyle {{\text{a}}_{2}}^{2}=\frac{{\tan \left( {\text{ψ}/2} \right)}}{{\tan \left( {\text{ψ}/2-{{\text{μ}}_{{\text{min}}}}} \right)}} | (9) |
since 0< y <1800, siny>0 for l2=0 , y-2mmin >0 or mmin< y /2. In other words, the minimum transmission angle can not be better than y /2 for drag link proportions. Hence, as we decrease y, the maximum deviation of the transmission angle from 900 will tend to increase (when l=1, the mechanism will form a folded position i.e. the sum of the lengths of the longest and shortest link lengths will be equal to the sum of the two intermediate link lengths)
Since \displaystyle {\text{a}_{3}}^{2}=\text{Z}\bar{\text{Z}} , we have:
| \displaystyle {{\text{a}}_{3}}^{2}=\frac{{{{{\left( {{{\text{a}}_{2}}+1} \right)}}^{2}}}}{{\left( {\text{λ}+{{\text{e}}^{{\text{i}{{\text{μ}}_{{\text{min}}}}}}}} \right)\left( {\text{λ}+{{\text{e}}^{{\text{-i}{{\text{μ}}_{{\text{min}}}}}}}} \right)}} | (10) |
or
| \displaystyle {{\text{a}}_{3}}^{2}=\frac{{\sin \left( \text{ψ} \right)}}{{\sin \left( {2{{\text{μ}}_{{\text{min}}}}} \right)}}\left[ {\frac{{\tan \left( {\text{ψ}/2} \right)}}{{\tan \left( {\text{ψ}/2-{{\text{μ}}_{{\text{min}}}}} \right)}}-1} \right]=\frac{{\sin \left( \text{ψ} \right)}}{{\sin \left( {2{{\text{μ}}_{{\text{min}}}}} \right)}}\left( {{{\text{a}}_{2}}^{2}-1} \right) | (11) |
and a4 =la3. Note that the resulting mechanism must be checked for movability.
Example 4.5.
Determine the four-bar mechanism with drag-link proportions for which for half a revolution of the input link the output link rotates by 1500. The minimum transmission angle must be greater than 450. Let the distance between the cranks be equal to 100 mm
Taking y=1500 and mmin=450 and a1=100 mm, from equations (8), (9) and (11):
\displaystyle {{\text{λ}}^{2}}=\frac{{\sin \left( {\text{150}{}^\circ -90{}^\circ } \right)}}{{\sin \left( {150{}^\circ } \right)}}=1.73205\text{ }\Rightarrow \text{ λ}=1.31607
\displaystyle {{\text{a}}_{2}}^{2}=\frac{{\tan \left( {75{}^\circ } \right)}}{{\tan \left( {75{}^\circ -45{}^\circ } \right)}}=6.464101\text{ }\Rightarrow \text{ }{{\text{a}}_{2}}=2.54246
\displaystyle {{\text{a}}_{3}}^{2}=\frac{{\sin \left( {150{}^\circ } \right)}}{{\sin \left( {90{}^\circ } \right)}}\left( {\frac{{\tan \left( {75{}^\circ } \right)}}{{\tan \left( {75{}^\circ -45{}^\circ } \right)}}-1} \right)=2.73205\text{ }\Rightarrow \text{ }{{\text{a}}_{3}}=1.65289
a4 = λa3 = 2.17533
a4 =la3 =2.17533. When a1 =100 mm a2 =254 mm a3 =165 mm and a4=218 mm. According to Grashof’s rule, the mechanism is of drag-link proportions.