7.1 Four Link Mechanisms

A four-link mechanism with four revolute joints is commonly called a four-bar mechanism. Application of four-bar mechanisms to machinery is numerous. Some typical applications will involve:

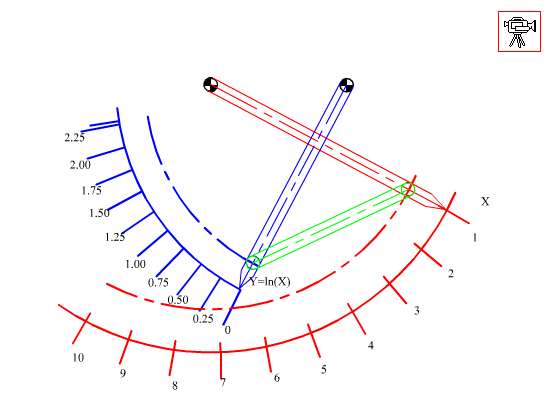
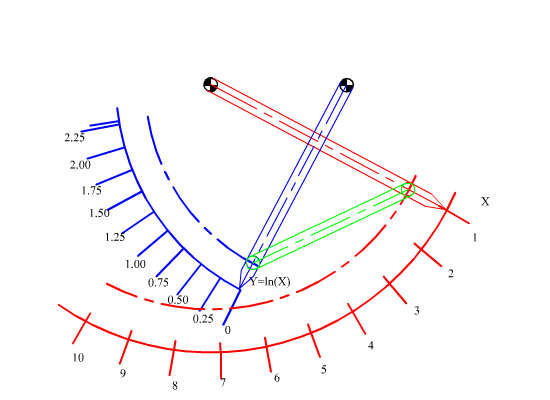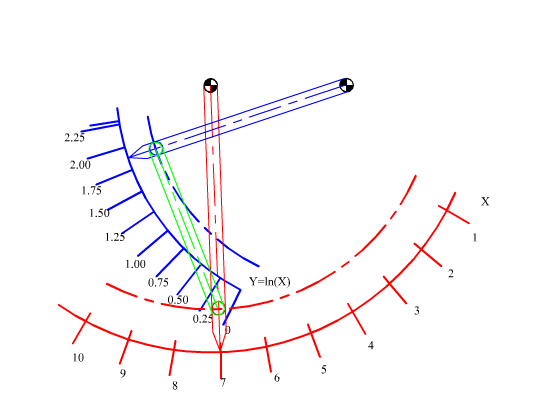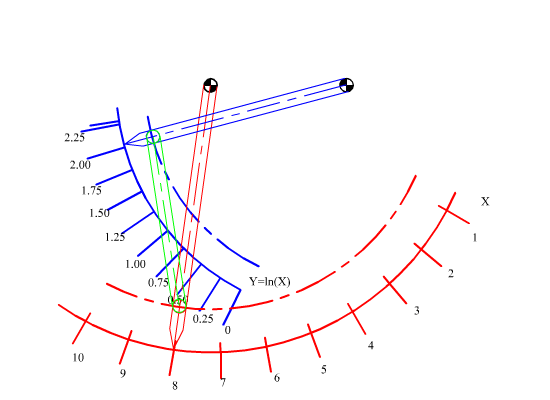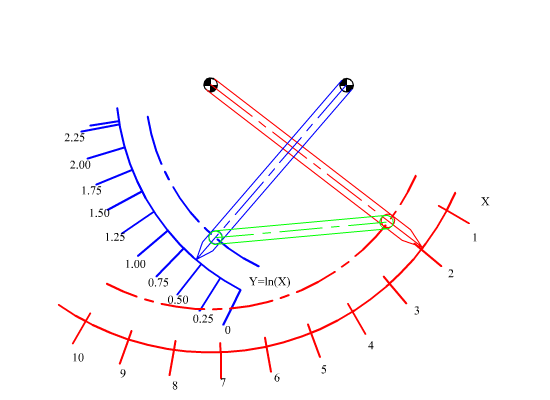
a) Correlation of the angular rotations of the links connected to the fixed link (commonly known as correlation of crank angles or function generation). In such applications we would like to have a certain functional relation such as q₁₄ = f(q₁₂) to be realised by the four-bar mechanism. A simple example will be to convert a linear scale to a logarithmic scale within a certain range.

b) Link that has no connection to the fixed link is known as the coupler link. A point on this link (which is known as the coupler point) will describe a path on the fixed link, which is called the coupler-point-curve. By proper choice of link dimensions useful curves, such as a straight-line or a circular arc, may be found. This coupler point curve can be used as the output of the four-bar mechanism (such as the intermittent film drive shown below

c) The positions of the coupler-link may be used as the output of the four-bar mechanism. As shown in figure below, the four-bar mechanism used for the dump truck requires that the center of gravity of the dumper to move on an inclined straight line while it is being tilted (why?).

The above applications can be solved by the methods of synthesis which is beyond the topic. In this chapter we shall discuss some basic characteristics of the four-bar.

7.1.1. Grasshof’s Theorem

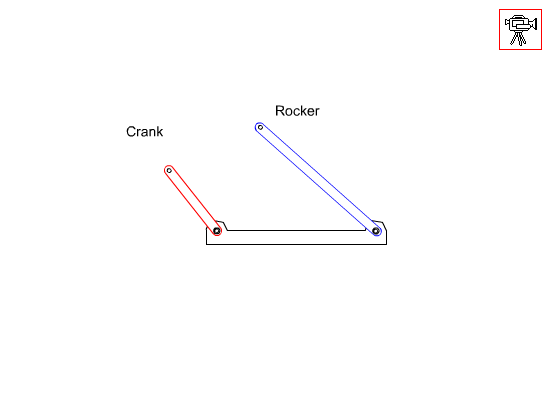
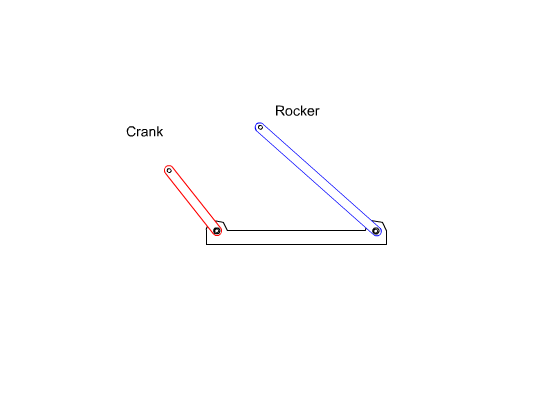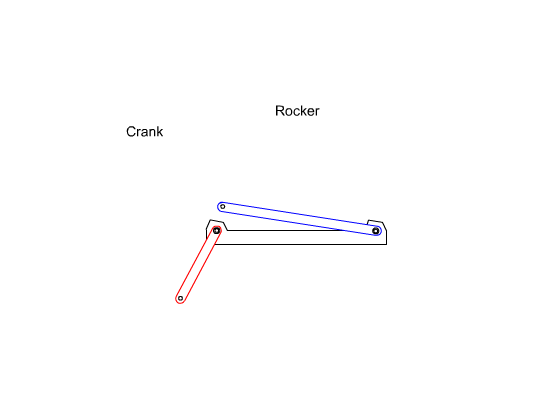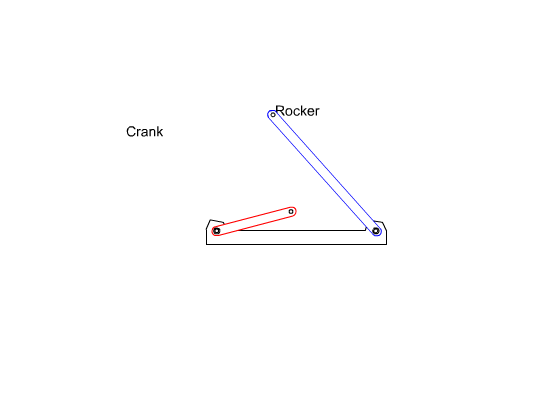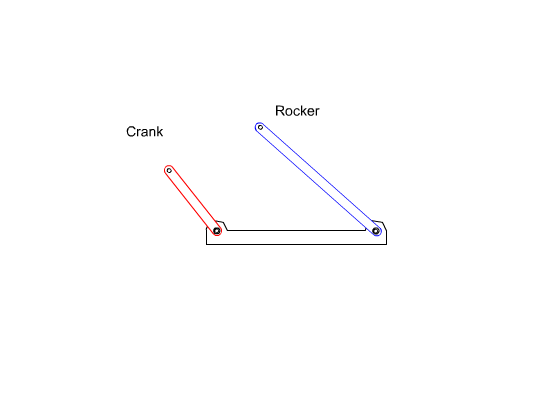
The motion characteristics of a-four-bar mechanism will depend on the ratio of the link length dimensions. The links that are connected to the fixed link can possibly have two different types of motion:

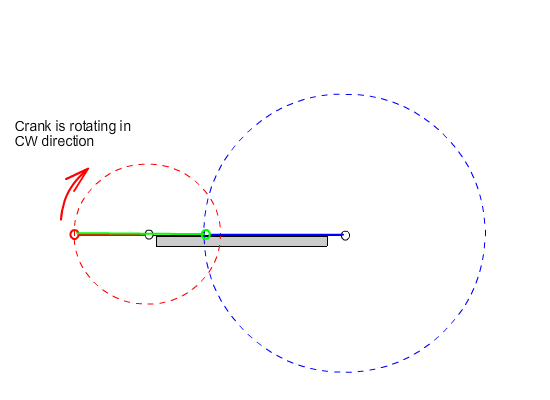
i) The link may have a full rotation about the fixed axis (we call this type of link crank)

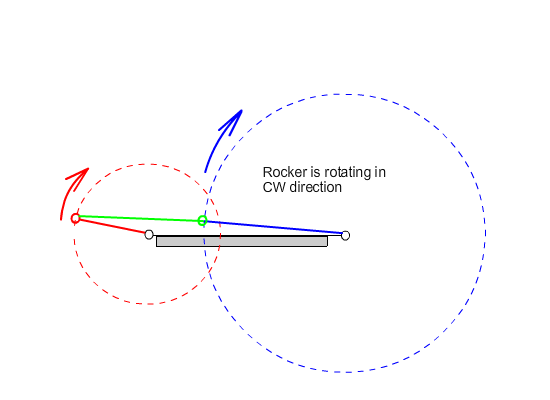
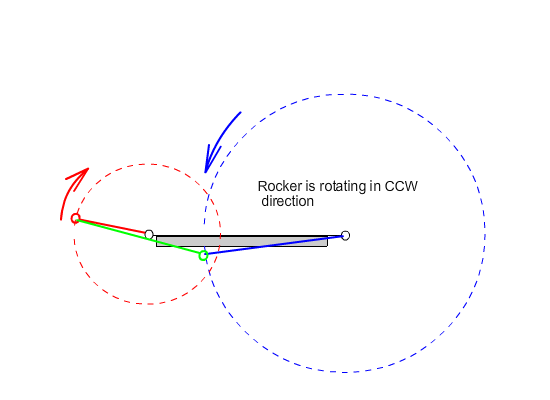
The link may oscillate (swing) between two limiting angles (we call this type of link rocker).

In a four-bar mechanism we can have the following three different types of motion:
i) Both of the links connected to the fixed link can have a full rotation. This type of four-bar is called double-crank or drag-link.
ii) Both of the links connected to the fixed link can only oscillate. This type of four-bar is called double-rocker.

iii) One of the links connected to the fixed link oscillates while the other has a full rotation. This type of four-bar is called crank-rocker.

The type of motion is a function of the link lengths. Grashof’s theorem (or Grashof’s rule) gives the criteria for these various conditions as follows:

Let us identify the link lengths in a four-bar chain as:
l = length of the longest link
s = length of the shortest link
p, q = length of the two intermediate links

The following statements are valid (stated without proof. One can prove these statements by using the input-output equation of a four-bar See Appendix AIII for the proof of the theorem):
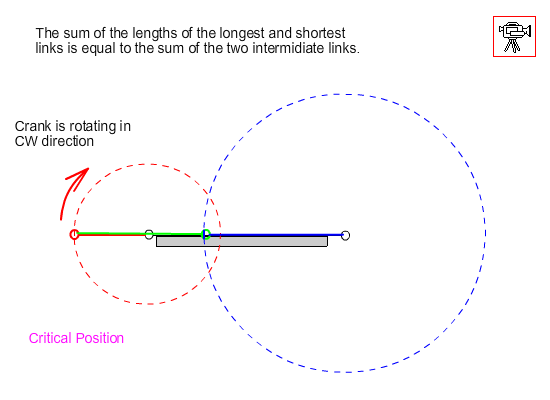
1. If l + s < p + q (if the sum of the lengths of the shortest and the longest links is less than the sum of the two intermediate links)

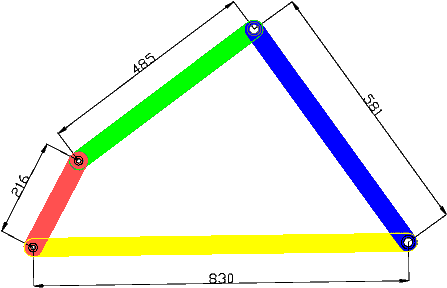
l = 830, s = 216 , p = 485 , q = 581

830 + 216 = 1046 < 485 + 581 = 1066

Then:

a, b) Two different crank-rocker mechanisms are possible. In each case the shortest link is the crank, the fixed link is either of the adjacent links.

c) One double-crank (drag-link) is possible when the shortest link is the frame.

d) One double-rocker mechanism is possible when the link opposite the shortest link is the frame.

If l + s > p + q (if the sum of the longest and the shortest link lengths is greater than the sum of the lengths of the two intermediate links).

Only double-rocker mechanisms are possible (four different mechanisms, depending on the fixed link).

If l + s = p + q the four possible mechanisms in (1) will result. However these mechanisms will suffer from a condition known as the change point. The center lines of all the links are collinear at this position. The follower linkage may change the direction of rotation. This is an undetermined position.

4. i) A parallelogram linkage is a special case of (3) where the opposite links are equal. All four-possible mechanisms are double-crank suffering from the condition of change point. It is possible to control the mechanisms at the change point by a configuration as shown

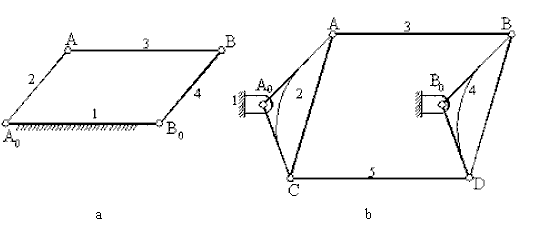
ii) A deltoid linkage is another special case of (3), in which two equal links are connected to two equal longer links as shown. With the long link as the frame a crank-rocker mechanism is possible. The frame as the short link may give a double-crank mechanism, in which the short link may rotate twice while the long link as the follower will rotate once (this mechanism is also known as the Galloway mechanism which was patented in 1844).

Note that if we multiply or divide all the link lengths by a constant, the ratio of the length of the links, hence the type of four-bar or the angular rotations of the links will not be effected. Therefore it is the ratio of the link lengths, not the link lengths as a whole, which determines the type of four-bar. If our interest is the rotation of the links only, the mechanisms with the same link length ratios will have the same motion characteristics no matter how big or small the mechanism is constructed (this scaling is like multiplying the loop equation by some constant).

Out of these types of four-bar mechanisms crank-rocker mechanism has a particular importance in machine design since a continuous rotation may be converted to an oscillation through this type of a four-bar (this statement does not necessarily mean that the other four-bar proportions are not used). We shall now discuss the four-bar mechanism with crank-rocker proportions and important problem related to it.

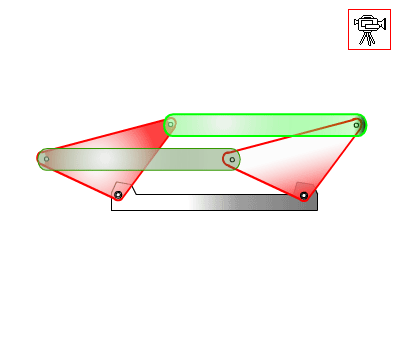
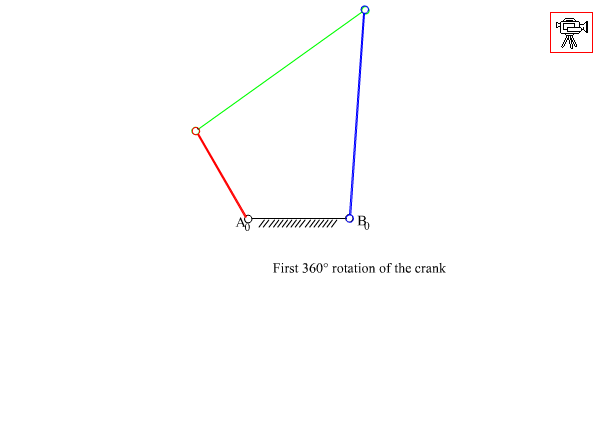
7.1.2. Dead-Center Positions of Crank-Rocker Mechanisms
In crank-rocker mechanisms the rocker oscillates between two limiting angles (In general, the crank is the input and rocker is the output). The positions of the mechanism when the rocker is at a limit position are called the dead-center positions of the four-bar. We can also define the dead centre position by considering the velocity of the rocker at these limiting angles. Since the rocker is moving in one direction before it reaches the limiting angle and since it moves in opposite direction after it passes this limit position, the velocity of the rocker at the limiting position must be zero. Hence, we can define a dead-center position as the position in which the rocker has instantaneously zero velocity. Consider a crank-rocker mechanism at an arbitrary position. Assuming that the crank is rotating with a speed ω₁₂, the angular velocity of the rocker is (refer to the velocity analysis of a four-bar mechanism):

$\displaystyle {\text{ω}_{{14}}}=\frac{{{\text{a}_{2}}}}{{{\text{a}_{4}}}}\frac{{\sin \left( {{\text{θ}_{{12}}}-{\text{θ}_{{13}}}} \right)}}{{\sin \left( {{\text{θ}_{{14}}}-{\text{θ}_{{13}}}} \right)}}{\text{ω}_{{12}}}$

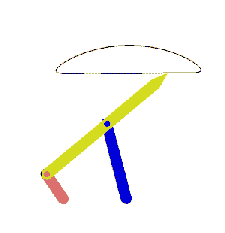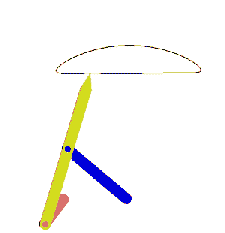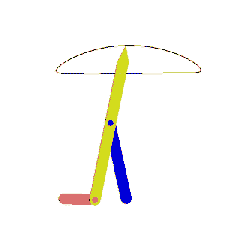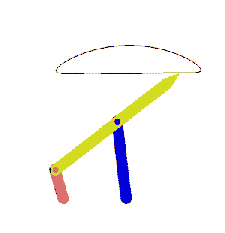
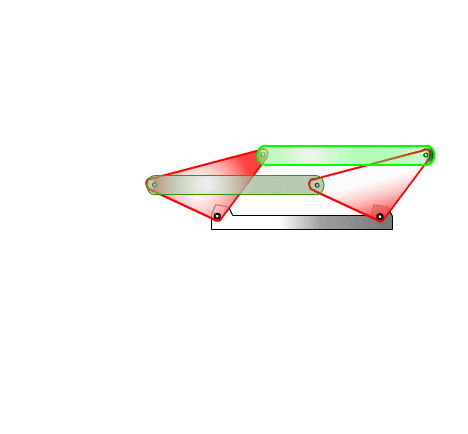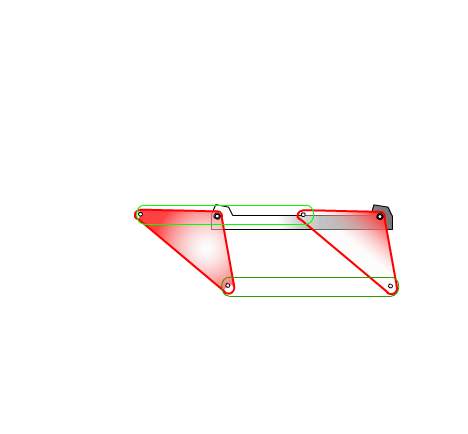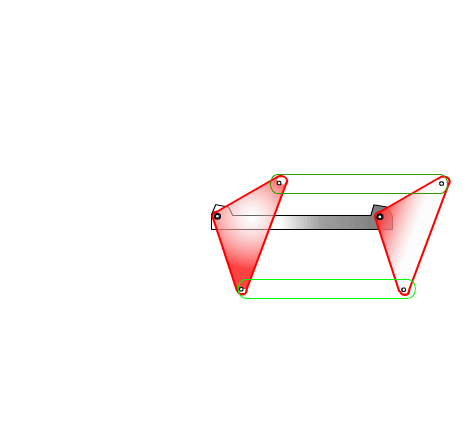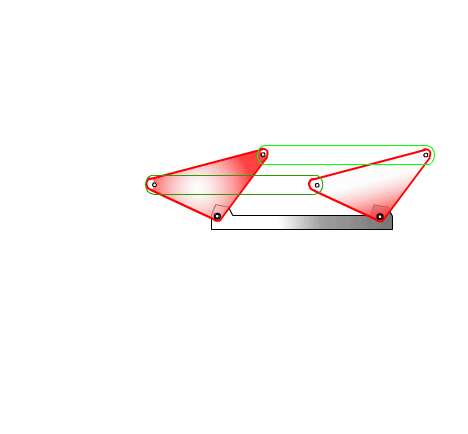
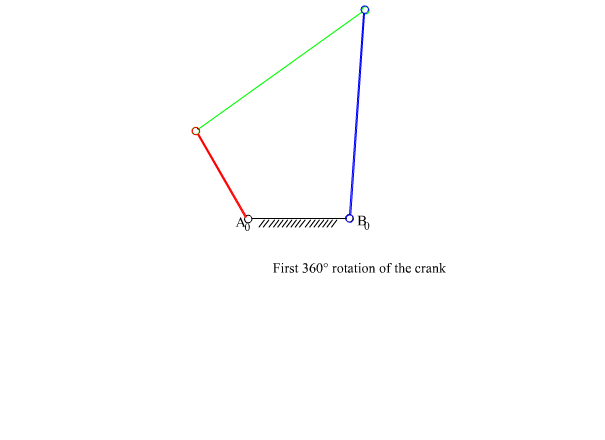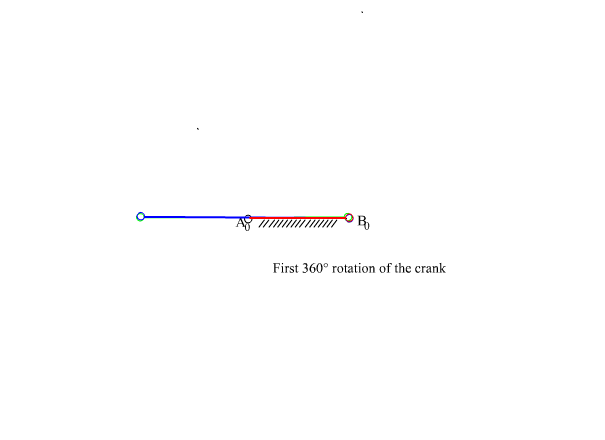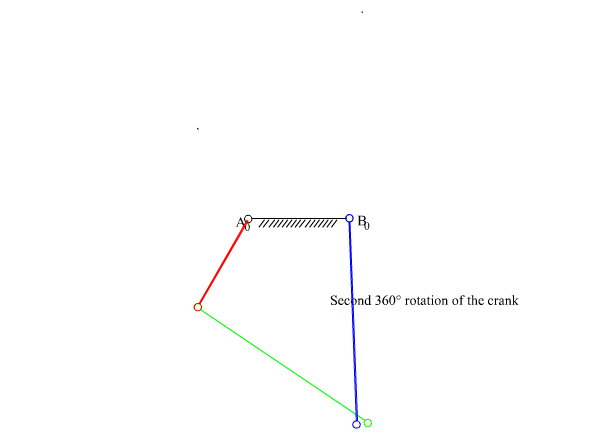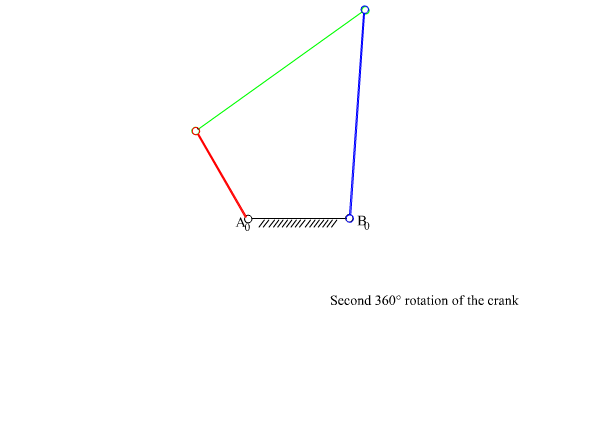
From this equation we can state that the rocker angular velocity will be zero when sin(q₁₂ – q₁₃) = 0 or when q_12 –q₁₃ = 0 or π. At these positions the coupler and crank angles are equal or differ by π (the coupler and the crank are collinear along the same line in extended or folded position). Hence we obtain the two limiting positions of the rocker as shown below.

Extended dead-center position is when the crank and the coupler links are extended (q₁₂ = q₁₃) and folded dead-center position is when the crank and the coupler are folded on top of each other (q₁₃ = q₁₂ + π). The oscillation angle of the rocker between the dead-center positions and measured from the extended dead-center to the folded dead-center position is called the swing angle, y. There is a corresponding crank rotation, ϕ. Sometimes, rather than the corresponding crank angle, time-ratio between the forward and reverse oscillations (strokes) is used. If we assume that the crank is rotating at a constant speed, we define the time ratio as:

$\displaystyle {\text{TR}=\frac{\text{time it takes for forward stroke}}{\text{time it takes for reverse troke}}=\frac{\text{ϕ}}{360°-\text{ϕ}}}$

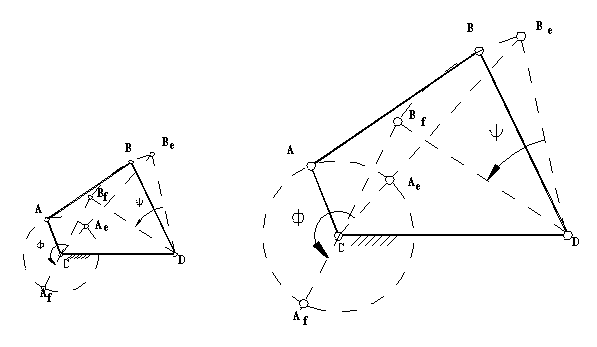
Forward stroke of the rocker is when the rocker is moving from extended to folded dead-center position in counterclockwise direction (In machinery forward stroke is the direction of motion during which the rocker is doing work. This definition need not correspond to the kinematic definition given above).
In case of four-bar mechanisms with crank-rocker proportions, if we take the mirror image of the mechanism with respect to the fixed link, we obtain another four bar mechanism of crank-rocker proportions and the same swing angle, y. However, when the crank rotates from the extended dead center position to the folded position in counter-clockwise direction the rocker will rotate in clockwise direction and the crank rotation is 360° – ϕ.
The reason why the limiting position is called the dead-centre position is that when the mechanism is at this position and if there is a force applied to the rocker, the mechanism will not move, e.g. the mechanism is locked with respect to an input motion or force from the rocker. This characteristics may sometimes be very useful.

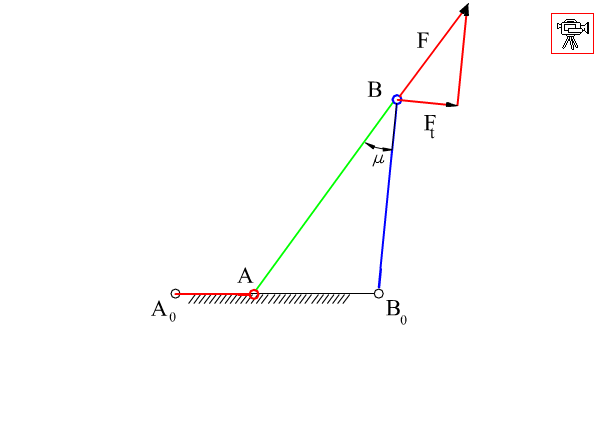
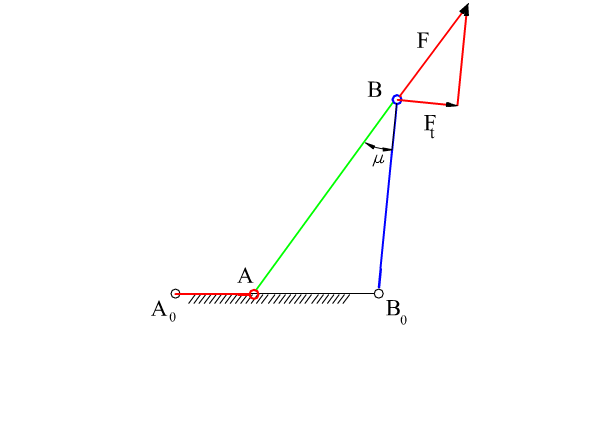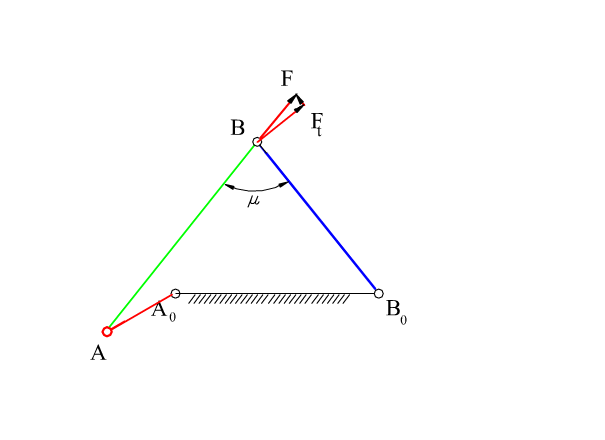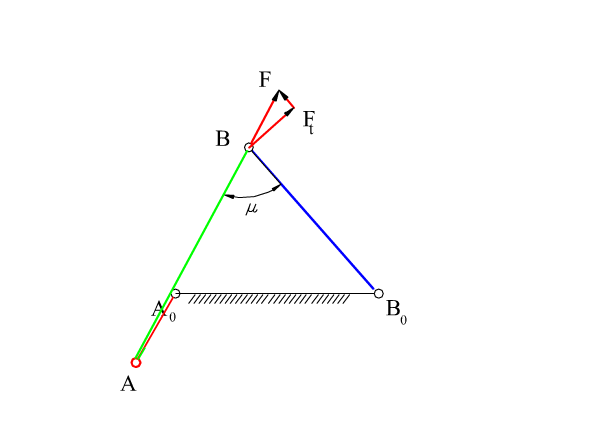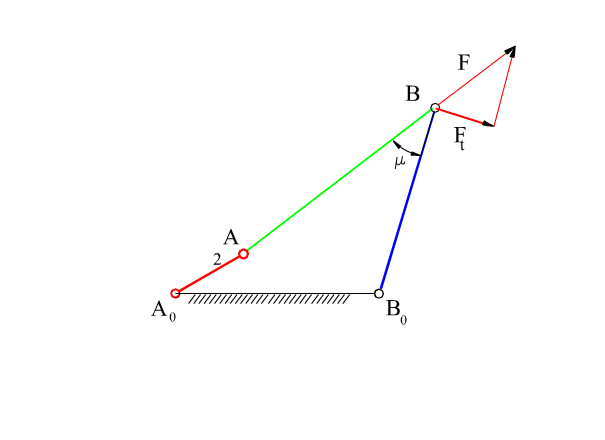
7.1.3. Transmission Angle

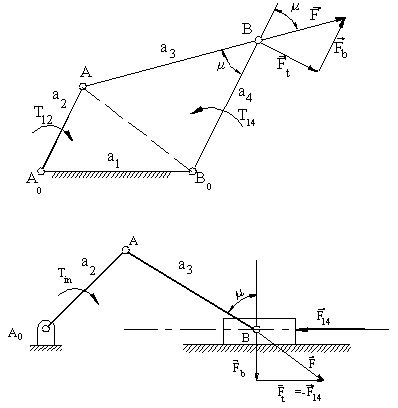
It is rather important to understand how the mechanism will function under loaded conditions in practice while the kinematic characteristics of the mechanism is being considered. By the performance of the mechanism we mean the effective transmission of motion (and force) from the input link to the output link. This also means that for a constant torque input, in a well performing mechanism we must obtain the maximum torque output that is possible and the bearing forces must be a minimum. Of course, torque and force are not the quantities that has been in the kinematics and whatever kinematic quantity we use to define the performance of the mechanism, this quantity will only approximate the static force characteristics of the mechanism. The dynamic characteristics, which is a function of mass and moment of inertia of the rigid bodies, may be several times more than the static forces and the behaviour of the mechanism under the dynamic forces cannot be predicted by kinematics. Still, some rule-of-thumb of the behaviour of the mechanism under load is better then none. Alt defined the transmission angle as:

$\displaystyle {\tan \text{μ}=\frac{\text{Force component tending to move driven link}}{\text{Force component tending yo apply pressure on driven link bearings}}=\frac{\text{F}_\text{t}}{\text{F}_\text{b}}}$

or, the transmission angle can be defined as:

$\displaystyle {\sin \text{μ}=\frac{\text{Force component tending to move driven link}}{\text{Total force applied to the driven link}}=\frac{\text{F}_\text{t}}{\text{F}}}$

The transmission angle for a four-bar mechanism and for a slider-crank mechanisms are shown below. It is a simple parameter in which neither the forces nor the velocities are taken into consideration. However, one can judge the performance of the mechanism in the kinematic design stage.

Clearly, the optimum value of the transmission angle is 90º. Since the angle will be constantly changing during the motion cycle of the mechanism, there will be a position at which the transmission angle will deviate most from 90º. In practice it has been found out that if the maximum deviation of the transmission angle from 90º exceeds 40º or 50º (depending on the type of application), the mechanism will lock. In certain cases this maximum deviation must be kept within 20º (e.g. reciprocating pumps) and in certain other applications maximum deviations of up to 70º may be permissible (e.g. aircraft landing gears). One must consider the practical application of a mechanism in order to give a limit to this deviation (whenever in doubt, try to keep this deviation to less that 40º or 50º).

One can express the transmission angle in terms of the crank angle and the link lengths as (by writing the cosine theorem for AB₀ using the triangles A₀AB₀ and ABB₀ and equating the length AB₀).

cosμ = (a₁² + a₂² − a₃² − a₄² + 2a₁a₂cosθ₁₂)/(2a₃a₄)

(1)

\displaystyle {\cos \text{μ}=\frac{{{{\text{a}}_{3}}^{2}+{{\text{a}}_{4}}^{2}-{{\text{a}}_{1}}^{2}-{{\text{a}}_{2}}^{2}}}{{2{{\text{a}}_{3}}{{\text{a}}_{4}}}}+\frac{{{{\text{a}}_{1}}{{\text{a}}_{2}}}}{{{{\text{a}}_{3}}{{\text{a}}_{4}}}}\cos {{\text{θ}}_{{12}}}}

(2)

The minimum and the maximum of the transmission angle can be determined by taking the derivative of the equation (2) with respect to θ₁₂ and equating to zero:

\displaystyle {\sin \text{μ} \frac{\text{dμ}}{\text{dθ}_{12}}=\frac{{{{\text{a}}_{1}}{{\text{a}}_{2}}}}{{{{\text{a}}_{3}}{{\text{a}}_{4}}}}\sin {{\text{θ}}_{{12}}} = 0}

(3)

The minimum and the maximum values of the transmission angle will be when sin(θ₁₂) = 0 or when θ₁₂ = 0 or π (when the crank and the fixed link are collinear in extended or folded positions). The minimum and the maximum value of the transmission angle for the four-bar mechanism will be given by:

\displaystyle {\cos \text{μ}_{\begin{smallmatrix} \text{min} \\ \text{max} \end{smallmatrix}}=\frac{{{{\text{a}}_{3}}^{2}+{{\text{a}}_{4}}^{2}-{{\text{a}}_{1}}^{2}-{{\text{a}}_{2}}^{2}}}{{2{{\text{a}}_{3}}{{\text{a}}_{4}}}} \pm \frac{{{{\text{a}}_{1}}{{\text{a}}_{2}}}}{{{{\text{a}}_{3}}{{\text{a}}_{4}}}}}

(4)

Δ₁ = |90° − μ_min| Δ₂ = |90° − μ_max|

Δ_max = max(Δ₁, Δ₂)

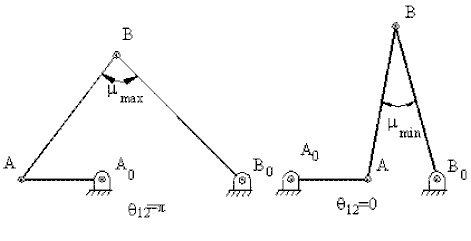
The critical transmission angle is either μ_min or μ_max, whichever deviates most from 90°. Sometimes, for the transmission angles greater than 90°, 180° – μ is used instead of μ for the value of the transmission angle. In such a case, there are two minimum values of the transmission angle (μ_min1 = μ_min, μ_min2 = 180° – μ_max). The most critical transmission angle is the minimum of m_min1 and m_min2. Note that the deviation of the transmission angle from 90° at the two extreme positions will be equal if:

a₁² + a₂² = a₃² + a₄²

(6)

Such four-bar mechanisms are known as centric four-bar. In centric four-bar mechanisms the time ratio is unity (the crank rotation between dead-centers is 180°) and they will have a better force transmission characteristics as compared with the other crank-rocker proportions.

Example:

Determine the swing angle, corresponding crank rotation and the maximum deviation of the transmission angle from 90⁰ for the four-bar mechanism whose link lengths are: a₂ = 4, a₃ = 8, a₄ = 6, a₁ = 7.

Since the sum of the longest and the shortest link lengths (4 + 8 = 12) is less then the lengths of the two intermediate links (6 + 7 = 13) the mechanism is of crank-rocker type and link 2 is the crank. At the dead center positions since the crank and the coupler links are collinear, the four-bar mechanism is of triangular form. Applying the cosine theorem for the extended dead-center:

$\displaystyle \cos \text{β}=\frac{{{{{\left( {8+4} \right)}}^{2}}+{{7}^{2}}-{{6}^{2}}}}{{2\cdot 7\cdot \left( {8+4} \right)}}=\frac{{157}}{{168}}=0.934524$

or β = 20.85° and

$\displaystyle \cos \left( {\text{π}-{{\text{ψ}}_{1}}} \right)=\frac{{{{7}^{2}}+{{6}^{2}}-{{{\left( {8+4} \right)}}^{2}}}}{{2\cdot 7\cdot 6}}=\frac{{-59}}{{84}}=-0.702381$

or ψ₁ = 45.38°. For the folded dead-center:

$\displaystyle \cos \left( {\text{β}+\text{ϕ}-\text{π}} \right)=\frac{{{{{\left( {8-4} \right)}}^{2}}+{{7}^{2}}-{{6}^{2}}}}{{2\cdot 7\cdot \left( {8-4} \right)}}=\frac{{29}}{{56}}=0.517857$

or ϕ = 217.96° and

$\displaystyle \cos \left( {\text{π}-{{\text{ψ}}_{1}}-\text{ψ}} \right)=\frac{{{{7}^{2}}+{{6}^{2}}-{{{\left( {8-4} \right)}}^{2}}}}{{2\cdot 7\cdot 6}}=\frac{{69}}{{84}}=0.821429$

or ψ = 99.85°. The maximum and the minimum transmission angle is:

$\displaystyle {\cos \text{μ}_{\begin{smallmatrix} \text{min} \\ \text{max} \end{smallmatrix}}=\frac{{{{6}^{2}}+{{8}^{2}}-{{7}^{2}}-{{4}^{2}}}}{{2\cdot 6\cdot 8}}\pm \frac{{4\cdot 7}}{{6\cdot 8}}=\frac{{35}}{{96}}\pm \frac{{28}}{{48}}=0.364583\pm 0.583333}$

μ_min = 18.57° (Δ1 = 71.43°) and μ_max = 102.64° (Δ₂ = 12.64°)

μ_min = 18.57° (D₁ = 71.43°) and μ_max = 102.64° (D₂ = 12.64°). since μ_min deviates most from 90°, μ_min is the critical transmission angle.

7.1 Four Link Mechanisms

The Classical Transmission Angle Problem

Design of Drag-link Mechanisms with Optimum Transmission Angle