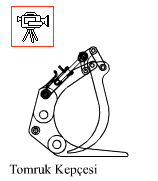
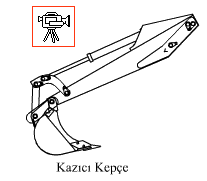
2.5 Mekanizmaların ve Kinematik Zincirlerin Enümerasyonu

“Enümerasyon” listeleme veya sayma olarak dilimize çevrilebilir. Kinematik açıdan enümerasyon önceden belirlenmiş kriterleri sağlayan kinematik zincirlerin veya mekanizmaların belirlenmesidir. Mekanizmaların enümerasyonu için çeşitli matematiksel yöntemler bulunmaktadır (çizge kuramı gibi). Burada sadece basit enümerasyon problemleri gösterilecektir.

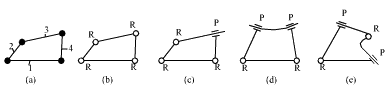
Enümerasyona bir örnek olarak Grübler denklemini sağlayan (yani, bir serbestlik dereceli, düzlemsel, kayar veya döner mafsallara sahip mekanizmalar) ve en az uzva sahip mekanizmaların listelenmesini ele alalım. Minimum uzuv sayısı 4 olmalıdır, çünkü iki elemanlı uzuv sayısı en az dörttür. Mafsal tipi gözardı edilir ise 4 uzvun dört mafsal ile tek bir şekilde bağlanabileceği görülür Her bir mafsalın döner veya kayar olabileceği düşünülür ise, 4 değişik zincir oluşturulabilecektir (Şekil b, c, d ve e). Kinematik zincirde üç veya dört kayar mafsal bulunamaz (neden?). Bu dört zincir elde edildikten sonra, değişik uzuvları sabitleyerek değişik mekanizmalar elde edilebilir.

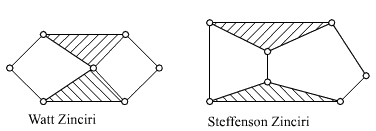
Dört uzuvlu mekanizmalardan sonra Grübler denklemini sağlayan mekanizmalarda 6 uzuv olabilir (5 uzuv olamaz çünkü Grübler denklemini sağlayan mekanizmalarda uzuv sayısı çift olmalıdır). Bu durumda mafsal sayısı, j, 7 olması gerekir. Grübler denklemi için çıkardığımız sonuçlara göre uzuvlardan 4ü iki elemanlı, 2 si ise üç elemanlı olmalıdır (2j = 2l₂ + 3l₃ ve j = 7 için l₂ = 4, l₃ = 2 bu denklemin tek tamsayılı ve pozitif değerli çözümüdür). Bu uzuvlar yedi mafsal ile (mafsal tipi göz önüne alınmadan) Şekilde gösterildiği gibi, iki değişik şekilde bir araya getirilebilir. “Watt Zinciri” olarak adlandırılan birinci zincirde iki üç kinematik elemanlı uzuv birbirlerine bağlı iken “Steffenson Zinciri” olarak adlandırılan ikinci zincirde ise üç kinematik elemanlı uzuvlar birbirlerine bağlı değildir (tarihsel olarak Bu iki zinciri ilk bulan kişiler, Watt ve Steffenson, aynı zamanda endüstriyel devrimi başlatan buharlı makinelerin kaşifleridirler). Kinematik zincirler için belirtilmiş olan kurallara uyarak mafsallar kayar veya döner olabilir ve değişik uzuvlar sabitlendiğinde çok sayıda mekanizma elde edilir.

Watt ve Steffenson zincirlerinde bulunan üç kinematik elemanlı uzvun birinde veya her ikisinde iki mafsal arasında kalan uzuv boyutu sıfır alınır ise, zincirde bir veya iki mafsalın derecesi iki olur. Bu zincirler aşağıda gösterilmiştir. Bu zincirlere Watt ve Steffenson zincirlerinin özel boyutlu durumları diyeceğiz.

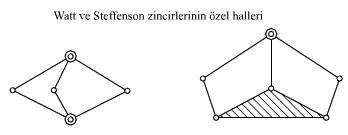
Mafsalların kayar ve döner olması ve değişik uzuvların sabitlenmesi ile çok değişik altı uzuvlu mekanizmalar elde edilebilecektir. Ancak bu mekanizmalar elde edilirken kayar ve döner mafsallardan oluşan kinematik zincirler için belirtilmiş olan sınırlamalar unutulmamalıdır.

Bir basit örnek olarak bir piston silindir ile tahrik edilen 6 uzuvlu mekanizmaları belirleyelim. Bu mekanizmalarda piston mutlaka sabit uzva bir döner mafsalla bağlı olsun ve ayrıca tüm diğer uzuvlar birbirlerine döner mafsallarla birleştirilsin.

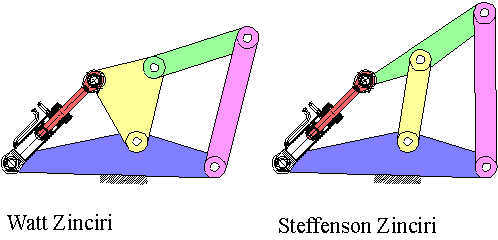
Piston silindir gurubu her biri iki elemanlı iki uzvun birbirlerine kayar mafsalla birleştirilmiş şekli olarak ele alınabilir. Bu durumda piston-silindir gurubu gerek Watt ve gerek Steffenson zincirlerinde birbirlerine bağlı iki elemanlı iki uzvun yerini alacaktır. Steffenson zincirinde bu grubun yerleştirilebileceği yer tektir. Watt zincirinde ise iki değişik yere yerleştirilebilir ise de, mekanizma simetrik olduğundan fark etmeyecektir. Pistonun sabit uzva bir döner mafsalla bağlı olması gerektiğinden her iki zincirde de üç elemanlı uzuvlardan birisi sabit olacaktır. Sonuç yukarıda görülmektedir.

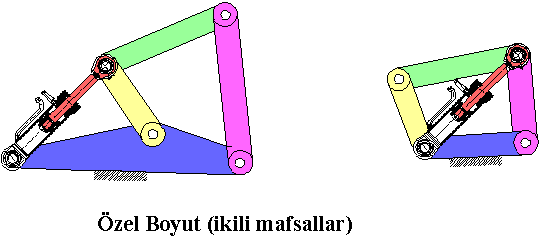
Üç elemanlı uzuvlardan birisinin veya her ikisinin mafsallar arasında uzaklığı sıfıra indirilmesi durumunda yukarıda gösterilen mekanizmalar elde edilecektir (mekanizma uzuv boyutları uygulamaya göre farklı şekiller alacaktır). Pratikte kamyon damperleri, beton pompalarının bomları, yükleyiciler, kepçeler elde edilen bu mekanizmaların uygulamasıdır. İki örnek aşağıda görülmektedir.