3.6 Step-Wise Solution of the Loop Closure Equation

As shown in the previous section, for simple mechanisms the solution of the loop closure equations reduces to the solution of a triangular relation. The triangular relations can as well be solved analytically. In this approach, rather than obtaining an explicit function between the input variable and other position variables, our aim will be to obtain a set of equations which, when solved in steps, will yield the value of all the unknown variables. Such a solution is a closed form solution and, furthermore, it is very suitable for a numerical solution using a computer, programmable calculator, or even on a simple calculator.

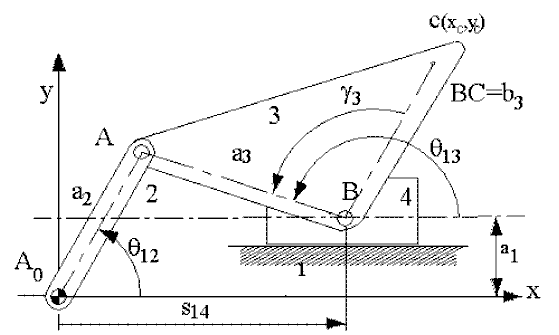
As a first example, consider a problem in which we want to determine the position of all the links of an off-set slider-crank mechanism shown below for different crank angles q₁₂. The link lengths denoted by a₁, a₂, a₃ are known.

The vector loop equation is:

A₀A = A₀B + BA

In rectangular form, these vectors can be written as:

A₀A = a₂(cosθ₁₂i + sinθ₁₂j)

A₀B = xi + a₁j

BA = a₃(cosθ₁₃i + sinθ₁₃j)

Equating x and y components separately, the loop closure equation will yield two scalar equations:

a2cosθ12 = s14 + a3cosθ13	(1)
a2sinθ12 = a1 + a3sinθ13	(2)

Rewriting these equations:

sinθ13 = (a2sinθ12 − a1)/a3	(3)
s14 = a2cosθ12 − a3cosθ13	(4)

For a given value of the input variable, θ₁₂, one can solve for θ₁₃ from (3) and substitute the values of θ₁₃ and θ₁₂ into equation (4) to obtain the corresponding value of s₁₄. The variable s₁₄ can be solved only after θ₁₃ is solved from (c). If we are to determine the co-ordinates of a point C (x_c, y_c), we can write:

xC = s14 + b3cos(θ13 − γ3)	(5)
yC = a1 + b3sin(θ13 − γ3)	(6)

Again equations (5) and (6) can be solved only after equations (3) and (4) are solved.

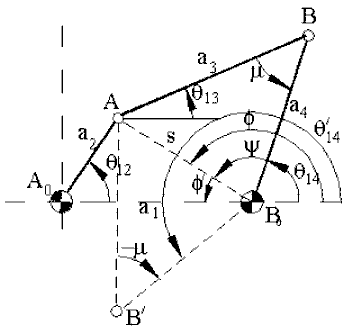
Since the scalar equations obtained from the loop closure equations are non-linear,  the method of solution will differ from one mechanism to the other. The method used for the analysis of a four-bar is known as the Raven’s Method. In the four-bar mechanism shown above, the link lengths (a₁, a₂, a₃, a₄) are given. We would like to determine the position of all the links for a given value of the input variable, q₁₂.

Similar to the method used in geometrical analysis, first consider the triangle  A₀AB₀. Since the two sides (a₁, a₂) and the included angle (q₁₂) are known, for this triangle the length of the third side (AB₀ = s) and angle ϕ of the triangle can be determined. Note that the length, s, and angle ϕ are variable. Using the cosine theorem:

s = \displaystyle \sqrt{{{{\text{a}}_{1}}^{2}+{\text{a}_{2}}^{2}-2{\text{a}_{1}}{{\text{a}}_{2}}\cos{{\text{θ}}_{{12}}}}}	(1)
ϕ′ = cos-1 \displaystyle \left[ {\frac{{{{\text{a}}_{1}}^{2}+{{\text{s}}^{2}}-{{\text{a}}_{2}}^{2}}}{{2{{\text{a}}_{1}}\text{s}}}} \right]     (ϕ = π − ϕ′)	(2)

Another form of calculating s and ϕ′, especially when a calculator has polar-to-rectangular conversion key, is to equate the x and y components:

s cosϕ = a2cosθ12 − a1 (horizontal component of B0A)	(1′)
s sinϕ = a2sinθ12 (vertical component of B0A)	(2′)

Now, if the values on the right-hand side of these equations are determined and if a rectangular-to-polar conversion is made, one will obtain s and ϕ as the output directly. This will give the correct quadrant for the angle ϕ at every instant. In computers a similar result can be obtained by using inverse tangent function with double argument (ATAN2 (x_s, y_s)) to obtain the correct quadrant for ϕ.

Referring to the triangle ABB₀ and applying cosine theorem:

μ = cos-1 \displaystyle \left[ {\frac{{{{\text{a}}_{3}}^{2}+{{\text{a}}_{4}}^{2}-{{\text{s}}^{2}}}}{{2{{\text{a}}_{3}}{{\text{a}}_{4}}}}} \right]	(3)
ψ = cos-1 \displaystyle \left[ {\frac{{{{\text{a}}_{4}}^{2}+{{\text{s}}^{2}}-{{\text{a}}_{3}}^{2}}}{{2{{\text{a}}_{4}}\text{s}}}} \right]	(4)

The magnitudes of ϕ′ and ψ are both less than 180° and ψ is always positive. If equations (1) and (2) are used,  than the sign of f’ must be checked (if you use rectangular-to-polar conversion the calculator gives the correct quadrant). The sign of sinϕ′ must be of the same sign as sinθ₁₂. The plus or minus sign for m refers to two different solutions of a four-bar mechanism as shown in the figure. The angle μ is known as the “transmission angle” whose importance is explained in Chapter 7.

The unknown position variables θ₁₃ and θ₁₄ can be easily determined as:

θ14′ = ϕ + ψ	(5′)
θ13′ = θ14 + μ	(6′)

Hence, we have obtained a set of equations which must be solved in steps.

In case of an inverted slider-crank mechanism shown below, the equations for the total position analysis are:

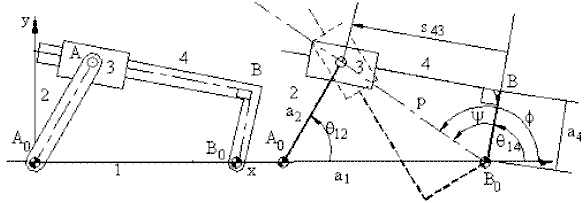
In case of an inverted slider-crank mechanism shown above, the equations for the total position analysis are:

p cosϕ = a2cosθ12 − a1	(1)
p sinϕ = a2sinθ12	(2)

(when solving with a calculator, use P – R conversion to determine p and ϕ)

ψ = cos-1(a4/p) s = \displaystyle \sqrt{{{{\text{p}}^{2}}-{{\text{a}}_{4}}^{2}}} θ14 = ϕ ± ψ	(3)
	(4)
	(5)

The derivation of these equations is left as an exercise (As a hint, the solution of the two triangles A₀AB and AB₀B in steps results with the above equations).

In great many mechanisms, the stepwise solution will require the solution of four-bar, slider-crank or inverted slider-crank loops in steps. For example, the quick-return mechanism shown below links 1, 2, 3 and 4 form an in-line inverted slider-crank mechanism while links 1, 4, 5 and 6 form a slider-crank mechanism. For a given value of the input variable, θ₁₂, the angle θ₁₄ and s can be determined. In case of the slider-crank mechanism, with θ₁₄ as the input variable, the position variables θ₁₅ and s₆ are found. In such an analysis, one must be concerned with the reference axes and how the variables are to be measured with respect to the reference axes.

 

 

 

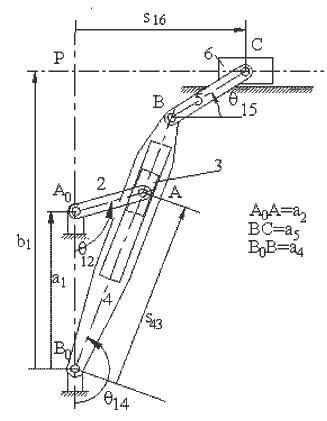
s₄₃cosθ₁₄ = a₂cosθ₁₂ − a₁

s₄₃sinθ₁₄ = a₂sinθ₁₂

θ₁₅ = sin^-1 \displaystyle \left[ {\frac{{{{\text{a}}_{4}}\cos{{\text{θ}}_{{14}}}+{{\text{b}}_{1}}}}{{{{\text{a}}_{5}}}}} \right]

s₁₆ = a₄sinθ₁₄ + a₅cosθ₁₅

 

 

The first two equations are the solution of the triangle A₀AB₀. The last two equations are the solution of the slider crank mechanism formed by links 1, 4, 5 and 6.

Example:

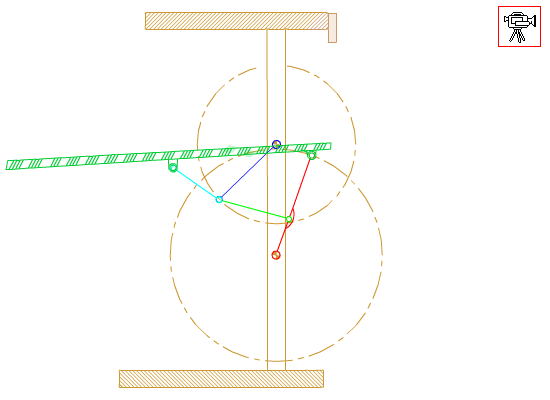
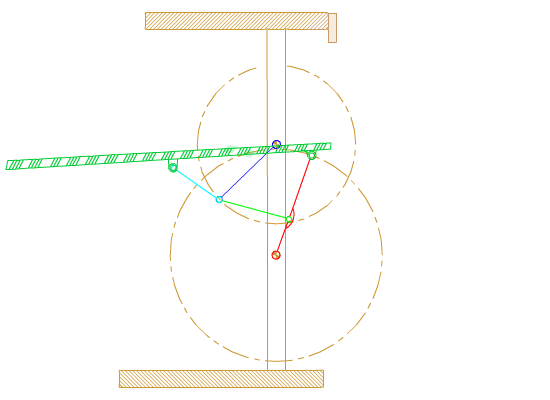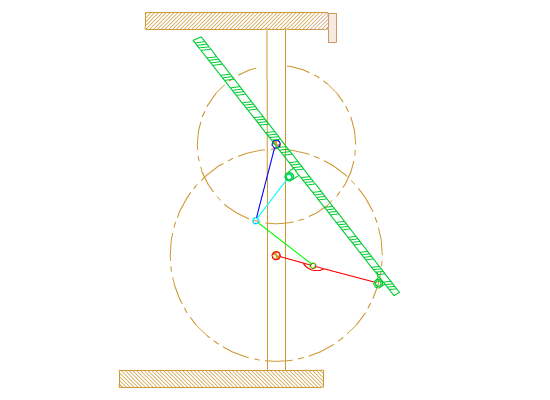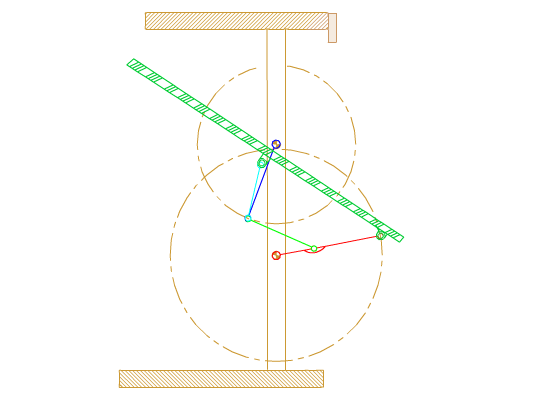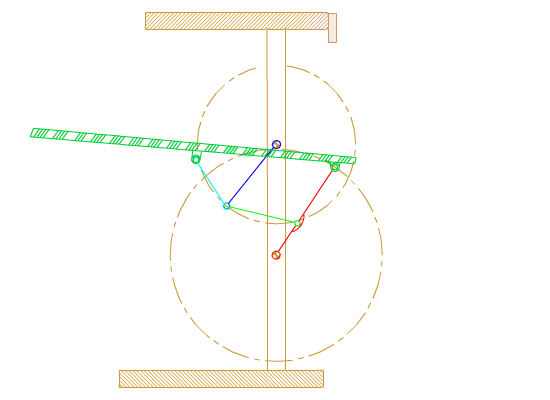
Consider the six link mechanism shown which is used as a garage door. We are to determine the position of the links when the input crank angle θ₁₂ is given. Let |A₀B₀| = a₁;  |A₀A| = a₂;  |A₀D| = b₂;  |AB| = a₃;  |BC| = b₅;  |BB₀| = a₄;  |CD| = a₆.

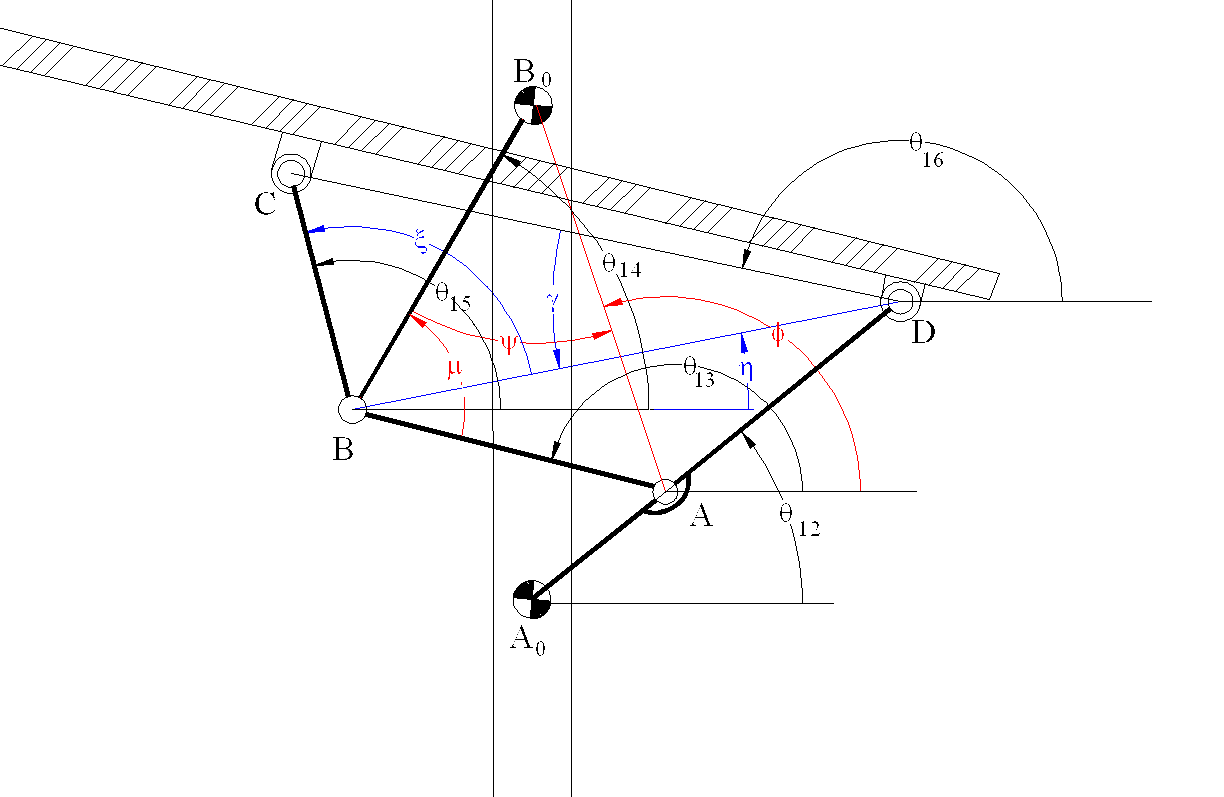
Noting that the links 1, 2, 3, 4 (A₀ABB₀) form a four-bar mechanism, referring to the equations derived for the four-bar:

     s cosϕ = −a₂cosq₁₂ : Horizontal component of AB₀ = x_s

     s cosϕ = −a₂cosq₁₂ + a₁ : Vertical component of AB₀ = y_s

     |B₀A|  = s = \displaystyle \sqrt{{{\text{x}}_{\text{s}}}^2+{{\text{y}}_{\text{s}}}^2} ;    f = tan^-1(x_s; y_s)

μ = cos^-1 \displaystyle \left( {\frac{{{{\text{a}}_{3}}^{2}+{{\text{a}}_{4}}^{2}-{{\text{s}}^{2}}}}{{2{{\text{a}}_{3}}{{\text{a}}_{4}}}}} \right)

ψ = cos^-1 \displaystyle \left( {\frac{{{{\text{a}}_{4}}^{2}+{{\text{s}}^{2}}-{{\text{a}}_{3}}^{2}}}{{2{{\text{a}}_{4}}\text{s}}}} \right)

θ₁₄ = ϕ − ψ

θ₁₃ = π − μ + θ₁₄

ψ, ϕ and μ are as defined for the four bar mechanism in the figure. The coordinates of points B and D relative to an xy-frame with center A₀ are:

    x_D = b₂cosθ₁₂

    y_D = b₂sinθ₁₂

    x_B = −a₄cosθ₁₄

    y_B = a₁ − a₄sinθ₁₄

The distance BD and the angle it makes with the horizontal is:

|BD| = s′ = \displaystyle \sqrt{{\left({\text{x}}_{\text{D}}-{\text{x}}_{\text{B}}\right)}^2+{\left({\text{y}}_{\text{D}}-{\text{y}}_{\text{B}}\right)}^2}

η = atan2(x_D − x_B; y_D − y_B)

From the triangle BDC:

ξ = cos^-1 \displaystyle \left( {\frac{{{{\text{a}}_{5}}^{2}+{{\text{s}}^\prime}^{2}-{{{\text{a}}_{6}}^{2}}}}{{2{{\text{a}}_{5}}{{\text{s}}^\prime}}}} \right)

γ = cos^-1 \displaystyle \left( {\frac{{{{\text{a}}_{6}}^{2}+{{\text{s}}^\prime}^{2}-{{{\text{a}}_{5}}^{2}}}}{{2{{\text{a}}_{6}}{{\text{s}}^\prime}}}} \right)

and

θ₁₅ = η + ζ

θ₁₆ = η + π − γ

Hence all the unknown position variables are determined in steps.These equations are valid for every position of θ₁₂. Note that these equations can be solved in steps (one after another). If the independent variable was selected as the angle of the door θ₁₆, then these equations must be solved simultaneously.