3.7 Position Analysis of Mechanisms By Means of Complex Numbers

We have seen that complex number utilisation is a simple and powerful technique for expressing the loop closure equations. The analytical or numerical solution of planar mechanisms can be easily performed by simple algebraic manipulations in complex numbers.

Considering the four-bar mechanism shown below, the loop closure equation in vectorial form is:

A₀A + AB = A₀B₀ + B₀B

or in complex numbers:

a2eiθ12 + a3eiθ13 = a1 + a4eiθ14

(1)

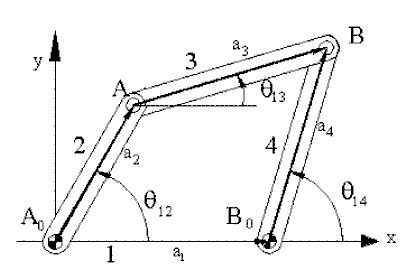
If we equate the real and imaginary parts of this equation separately, we obtain two scalar equations in three position variables (θ₁₂, θ₁₃ and θ₁₄). If one of the position variables is the input variable whose value is given, then we shall be able to solve for the values of the other two variables.

In complex plane, when we have an equation in complex numbers, the complex conjugate of the equation is also true (see Appendix I). The complex conjugate yields vectors which are the mirror image of the original vectors with respect to the real axis (x-axis); e.g. in case of a mechanism, if we place a mirror about the real axis, as we move the original mechanism its image will also move and corresponding to the original closed loop, the loop formed on the mirror image will also be closed at every position. Hence we obtain another loop closure equation in terms of complex numbers as:

a2e−iθ12 + a3e−iθ13 = a1 + a4e−iθ14

(2)

The original equation (1) and its complex conjugate (2) are the two independent equations in the complex plane (if we equate the real and imaginary parts of these equations they will yield the same two scalar equations in the real plane).

In general, the loop closure equations yield a non-linear relation between the position variables. The closed form solution of these equations is not straight forward. For simple mechanisms, utilising complex algebra one can solve for the unknown position variables. An iterative numerical solution of these equations will be explained in Section 2.5. In this section, closed form solution of the loop closure equations for simple mechanisms will be explained only.

Using the equations (1) and (2), if we are to find θ₁₄ as a function of θ₁₂, we have to eliminate θ₁₃ from the above equations. We can write the loop closure equations in the form:

a3eiθ13 = a1 + a4eiθ14 − a2eiθ12	(3)
a3e−iθ13 = a1 + a4e−iθ14 − a2e−iθ12	(4)

Multiplying equations (3) and (4):

a32ei(θ13 − θ13) = (a1 + a4eiθ14 − a2eiθ12)(a1 + a4e−iθ14 − a2e−iθ12)

(5)

Noting e^{i(θ − θ)} = eⁱ⁰ =1:

a32 = a12 + a42 + a22 + a1a4[eiθ14 − e−iθ14] − a1a2[eiθ12 + e−iθ12] − a2a4[ei(θ14 − θ12) − e−i(θ14 − θ12)]

(6)

Since cosθ = (e^iθ + e^−iθ)/2 equation (6) reduces to the form:

a₃² = a₁² + a₂² + a₄² + 2a₁a₄cosθ₁₄ − 2a₁a₂cosθ₁₂ − 2a₂a₄cos(θ₁₄ − θ₁₂)

or, dividing every term by 2a2a4:

K1cosθ14 − K2cosθ12 + K3 = cos(θ14 − θ12)

(7)

where K₁ = a₁/a₂ , K₂ = a₁/a₄ , K₃ = (a₁² + a₂² − a₃² + a₄² )/2a₂a₄

Equation (7) is called “Freudenstein’s Equation” which can be used for the synthesis of four-bar mechanisms. It gives an implicit relation between the position variables θ₁₄ and θ₁₂. In order to obtain an explicit expression for θ₁₄, Freudenstein’s equation can be written in the form:

K1cosθ14 − K2sinθ12 + K3 = cosθ12cosθ14 + sinθ12sinθ14

(8)

Substituting the trigonometric identities:

sinθ₁₄ = 2t/(1 + t²)     and     cosθ₁₄ = (1 − t²)/(1 + t²)

where t = tan(θ₁₄/2) (This is commonly known as half-tangent form of representation of the sine and cosine function).

Freudenstein’s equation results:

At2 + Bt + C = 0

(9)

where:

A = cosθ₁₂(1 − K₂) + K₃ − K₁

B = −2 sinθ₁₂

C = cosθ₁₂(1 + K₂) + K₃ + K₁

Equation (9) is a quadratic in terms of

\displaystyle \tan \left( {\frac{{{{\text{θ}}_{{14}}}}}{2}} \right)=\frac{{-\text{B}\pm \sqrt{{{{\text{B}}^{2}}-4\text{AC}}}}}{{2\text{A}}}

therefore:

\displaystyle {{{\text{θ}}_{{14}}}=2{{\tan }^{{-1}}}\left[ {\frac{{-\text{B}\pm \sqrt{{{{\text{B}}^{2}}-4\text{AC}}}}}{{2\text{A}}}} \right]}

(10)

Where the plus or minus sign refers to two different configurations of the four-bar mechanism. Also note that the coefficients of the quadratic (A, B and C) are functions of the link lengths and the input crank angle only. Therefore, if the input crank angle is given, θ₁₄ can be obtained from equation (10) directly.

One can perform a similar procedure to determine the coupler-link angle, θ₁₃, in terms of the input angle, θ₁₂. This is left as an exercise.

Another form of solving equation (8) is to rewrite it in the form:

(K1 − cosθ12)cosθ14 − sinθ14sinθ12 = K2cosθ12 − K3

(11)

If we let:

D cosϕ = K1 − cosθ12 D sinϕ = sinθ12

(12)

where

\displaystyle {\text{D}=\sqrt{{{{{\left( {{{\text{K}}_{1}}-\cos {{\text{θ}}_{{12}}}} \right)}}^{2}}+{{{\sin }}^{2}}{{\text{θ}}_{{12}}}}}=\sqrt{{1+{{\text{K}}_{1}}^{2}-2{{\text{K}}_{1}}\cos {{\text{θ}}_{{12}}}}}} \displaystyle {\text{ϕ} ={{\tan }^{{-1}}}\frac{{\sin {{\text{θ}}_{{12}}}}}{{{{\text{K}}_{1}}-\cos {{\text{θ}}_{{12}}}}}}

(13)

Equation (11) reduces to:

D cosϕ cosθ₁₄ − D sinϕ sinθ₁₄ = K₂cosθ₁₂ − K₃

Then using the trigonometric identity: cos (θ + ϕ) = cosθcosϕ − sinθsinϕ :

cos(θ14 + ϕ) = (K2 cosθ12 − K3)/D

(14)

or

θ14 = cos-1[(K2cosθ12 − K3)/D] − ϕ

(15)

When solving for ϕ in equation (13), one must remember that for a correct quadrant of the angle either the sign of the x and y components must be checked or double argument inverse tangent function must be used. In equation (15) the two different solutions for the inverse cosine function (= ±ϕ) will yield open or crossed configuration of the four-bar mechanism.

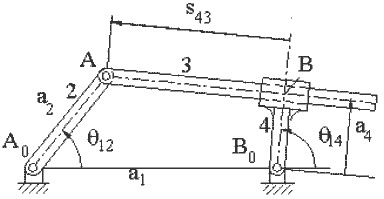
As another example for the solution of loop closure equations in complex numbers consider an inverted slider-crank mechanism where θ₁₄ is the input variable and θ₁₄ is the output variable. We would like to determine θ₁₄ as a function of θ₁₂.

Vector loop closure equation is: 

A₀A = A₀B₀ + B₀B + BA

  and in complex numbers:

a₂e^iθ₁₂ = a₁ + a₄e^iθ₁₄ + s₄₃e^{i(θ₁₄ + π/2)}

or

a2eiθ12 = a1 + a4eiθ14 + is43eiθ14

(1)

and its complex conjugate is:

a2e−iθ12 = a1 + a4e−iθ14 − is43e−iθ14

(2)

We would like to eliminate s₄₃ from the equations. Therefore:

is43eiθ14 = a2eiθ12 − a1 − a4eiθ14	(3)
is43e−iθ14 = a1 + a4e−iθ14 − a2e−iθ12	(4)

Taking the ratio of the two sides and cross-multiplying:

a₂e^{i(θ₁₂ − θ₁₄)} − a₁e^−iθ₁₄ − a₄ = a₁e^iθ₁₄ + a₄ − a₂e^{−i(θ₁₂ − θ₁₄)}

or

a2[ei(θ12 − θ14) + e−i(θ12 − θ14)]− a1[eiθ14 + e−iθ14] − 2a4 = 0

(5)

noting e^iθ + e^−iθ = 2cosθ:

a2cos(θ14 − θ12) − a1cosθ14 − a4 = 0

(6)

Using half-tangent form for cosq ₁₄ and sinq ₁₄ equation (6) reduces to a quadratic equation in t = tan(θ₁₄/2)  as

At2 + Bt + C = 0

(7)

where:

A = a₁ − a₄ − a₂cosθ₁₂

B = 2sinθ₁₂

C = a₂cosθ₁₂ − a₁ − a₄

The solution for Equation (7) can be obtained as in the four-bar example.

If we are to determine s₃₄ as a function of q₁₂, the loop closure equation and its complex conjugate can be written in the form:

(a₄ + is₄₃)e^iθ₁₄ = a₂e^iθ₁₂ − a₁

(a₄ − is₄₃)e^−iθ₁₄ = a₂e^−iθ₁₂ − a₁

Multiplying the two equations yields:

s₄₃² = a₁² + a₂² − a₄² − 2a₁a₂cosθ₁₂

In general, for closed form solutions, utilisation of half-tangent form for the trigonometric functions is preferred. The main reason is that the inverse sine and cosine functions are double valued and usually the inverse functions in calculators or computers yield only one of the values as the output (for y₁ = cos^-1(x), y₂ = sin^-1(x), y₃ = tan^-1(x), the range of function values are 0< y_l < p, −p/2< y₂ < p /2 and −p/2 < y₃< p /2 for any value of x). If one of these inverse functions are used, one must first determine the quadrant in which the variable angle lies for each position and then change the value obtained by adding or subtracting p. Because of this calculation difficulty, either half tangent form of the trigonometric functions or double argument inverse tangent (e.g. q = tan^-1(x, y)) or polar-to-rectangular conversion is used.