Bağlama Açısı En İyi Olan Çift Kol Mekanizması Tasarımı

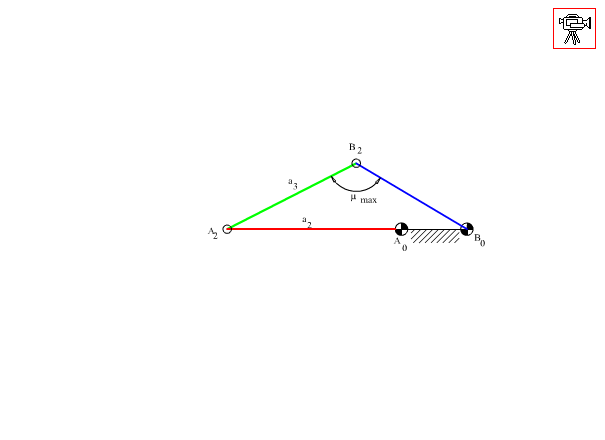
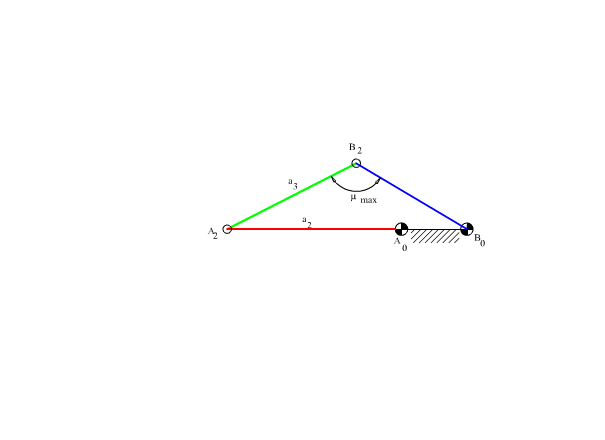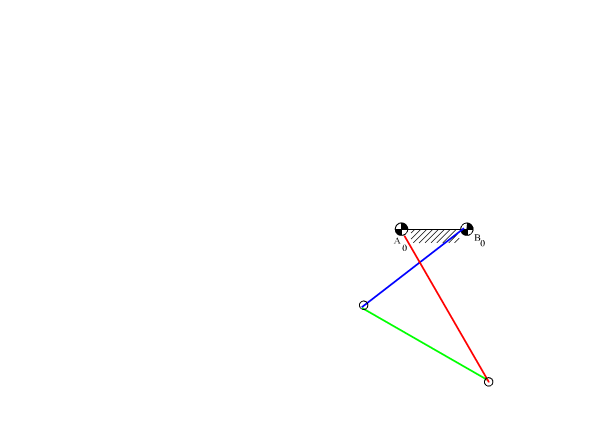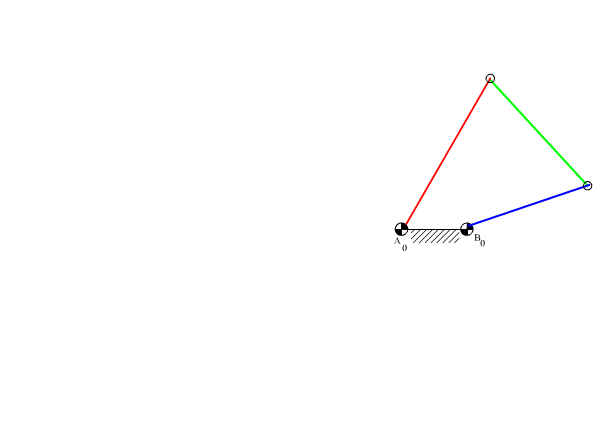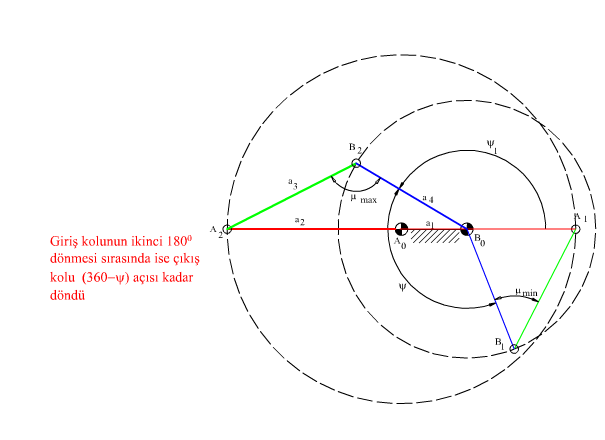
Çift kol mekanizması genel olarak düzgün bir dönme hareketini düzgün olmayan bir dönme hareketine dönüştürmek için kullanılır. Değişik hareket özellikleri için bazen bir kol-sarkaç mekanizması ile birlikte kullanılabilir (örneğin zaman oranını artırmak için bir çift-kol mekanizması ile bir kol-sarkaç mekanizmasının seri bağlanması ile elde edilen bir 6-çubuk mekanizması kullanılabilir). Şekilde çift kol oranlarında bir dört-çubuk mekanizması görülmektedir. Bağlama açısının 90° den sapmasının maksimum olduğu noktalar sabit uzuv ile giriş kolu olan krankın aynı doğrultuda olduğu konumlardır. Bağlama açısının dik açıdan yaptığı maksimum sapmanın azaltılabilmesi için bu iki sapma değerinin eşit olması gerekir (μ_max − 90° = 90° − μ_min).

Giriş kolunun 180° dönmesine karşı çıkış kolu bir ψ açısı kadar dönecek (ψ < 180° kabul edilecektir. Kalan ikinci 180° giriş kolu dönmesi sırasında çıkış kolu 360° − ψ kadar dönmesi gerekmektedir). Bağlama açısının en küçük değeri μ_min olsun. İki sınır değer şekilde görüldüğü gibidir. Bu iki sınır konum için bağlama açılarının dik açıdan sapmaları eşitlendikten sonra devre kapalılık denklemi yazılır ise:

−a₁ − a₂ + a₃e^{i(ψ₁ − π + μ_min)} = a₄e^iψ₁	(1)
−a₁ + a₂ + a₃e^{i(ψ₁ + ψ − μ_min)} = a₄e^{i(ψ₁ + ψ)}	(2)

elde edilir. Ayrıca bu maksimum ve minimum bağlama açısı değerlerinin birbirlerine eşit olması şartı kullanıldığında:

a₁² + a₂² = a₃² + a₄²

(3)

elde edilir. a₁ = 1 olarak alındığında λ = a₄/a₃ ve Z = a₃e^iψ₁ için denklem (1) ve (2)

−1 − a₂ − Ze^iμ_min = λZ	(4)
−1 + a₂ + Ze^{i(ψ − μ_min)} = λZe^iψ	(5)

olarak yazılabilir. Z parametresini (4) ve (5) denklemlerini kullanarak yok edersek

\displaystyle \frac{{1+{{\text{a}}_{2}}}}{{1-{{\text{a}}_{2}}}}=\frac{{\text{λ}+{{\text{e}}^{{\text{i}{{\text{μ}}_{{\text{min}}}}}}}}}{{{{\text{e}}^{{\text{iψ}}}}\left( {\text{λ}-{{\text{e}}^{{\text{i}{{\text{μ}}_{{\text{min}}}}}}}} \right)}}

(6)

elde edilir. Bu denklem

a₂[λcos(ψ/2) − i sin(ψ/2 − μ_min)] + i λsin(ψ/2) − cos(ψ/2 − μ_min) = 0

(7)

olarak yazılabilir. Denklemin sanal ve reel kısımlarını ayrı ayrı sıfıra eşitler, λ ve a₂ için çözüm yaparsak:

$\displaystyle {{\text{λ}}^{2}}=\frac{{\sin \left( {\text{ψ}-2{{\text{μ}}_{{\text{min}}}}} \right)}}{{\sin \left( \text{ψ} \right)}}$	(8)
$\displaystyle {{\text{a}}_{2}}^{2}=\frac{{\tan \left( {\text{ψ}/2} \right)}}{{\tan \left( {\text{ψ}/2-{{\text{μ}}_{{\text{min}}}}} \right)}}$	(9)

0< ψ <180° olduğundan sinψ > 0 ve λ² > 0 olacaktır ve ψ − 2μ_min > 0 veya μ_min < ψ/2 sonucu elde edilir. Farklı bir deyiş ile en küçük bağlama açısı değeri bir çift kol mekanizması için ψ/2 den daha iyi olamaz. Eğer ψ açısı küçülür ise, bağlama açısının 90° den sapması artacaktır (λ = 1 iken mekanizma katlanabilir bir konuma sahiptir, yani en kısa uzuv boyu ile en uzun uzuv boyu toplamı diğer iki uzuv boyu toplamına eşittir).

$\displaystyle {\text{a}_{3}}^{2}=\text{Z}\bar{\text{Z}}$ olduğundan a₃ uzuv boyutu:

\displaystyle {{\text{a}}_{3}}^{2}=\frac{{{{{\left( {{{\text{a}}_{2}}+1} \right)}}^{2}}}}{{\left( {\text{λ}+{{\text{e}}^{{\text{i}{{\text{μ}}_{{\text{min}}}}}}}} \right)\left( {\text{λ}+{{\text{e}}^{{\text{-i}{{\text{μ}}_{{\text{min}}}}}}}} \right)}}

(7)

(8) ve (9) numaralı denklemlerden a₂ ve λ değerleri kullanılır ise:

\displaystyle {{\text{a}}_{3}}^{2}=\frac{{\sin \left( \text{ψ} \right)}}{{\sin \left( {2{{\text{μ}}_{{\text{min}}}}} \right)}}\left[ {\frac{{\tan \left( {\text{ψ}/2} \right)}}{{\tan \left( {\text{ψ}/2-{{\text{μ}}_{{\text{min}}}}} \right)}}-1} \right]=\frac{{\sin \left( \text{ψ} \right)}}{{\sin \left( {2{{\text{μ}}_{{\text{min}}}}} \right)}}\left( {{{\text{a}}_{2}}^{2}-1} \right)

(11)

Ayrıca a₄ = λa₃ tür. Elde edilen sonuç mekanizma mutlaka Grashof kuralına göre kontrol edilmelidir.

Örnek:

Çift- kol oranında bir dört-çubuk mekanizmasında krankın ilk yarım tur dönüşünde çıkış kolunun 150° dönmesi istenilmekte ve minimum bağlama açısının 45° den fazla olması gerekmektedir. Sabit uzuv uzunluğu 100 mm olarak seçilmiştir.

ψ = 150°, μ_min = 45° ve a₁ = 100 mm olarak alındığında denklem (8), (9) ve (11) kullanılarak:

$\displaystyle {{\text{λ}}^{2}}=\frac{{\sin \left( {\text{150}{}^\circ -90{}^\circ } \right)}}{{\sin \left( {150{}^\circ } \right)}}=1.73205\text{ }\Rightarrow \text{ λ}=1.31607$

$\displaystyle {{\text{a}}_{2}}^{2}=\frac{{\tan \left( {75{}^\circ } \right)}}{{\tan \left( {75{}^\circ -45{}^\circ } \right)}}=6.464101\text{ }\Rightarrow \text{ }{{\text{a}}_{2}}=2.54246$

$\displaystyle {{\text{a}}_{3}}^{2}=\frac{{\sin \left( {150{}^\circ } \right)}}{{\sin \left( {90{}^\circ } \right)}}\left( {\frac{{\tan \left( {75{}^\circ } \right)}}{{\tan \left( {75{}^\circ -45{}^\circ } \right)}}-1} \right)=2.73205\text{ }\Rightarrow \text{ }{{\text{a}}_{3}}=1.65289$

a₄ = λa₃ = 2.17533

olur. a₁ = 100 mm alındığında a₂ = 254 mm, a₃ = 165 mm ve a₄ = 218 mm olacaktır. Grashof kuralına göre dört-çubuk mekanizması çift koldur. Sonuç şekilde görülmektedir.

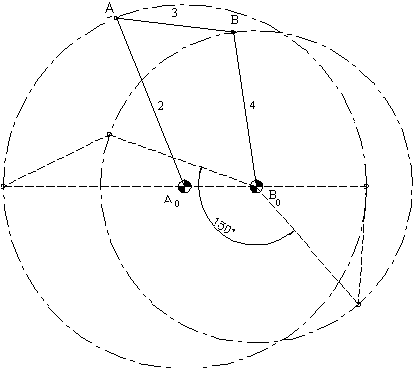
Yukarıda açıklanmış olan tasarım kolayca Excel programında yapılabilir. Excel kütüğü için tıklayınız.