4.2 Mekanizmalarda Hız ve İvme Analizi -3

Örnek:

Şekilde gösterilen mekanizmada pistonun (2 uzvu) yukarıya doğru sabit hızı v_B = v_2/1 = 180 mm/s dir. D noktasının hız ve ivmesini bulmamız istenmektedir. Aşağıda Excel programları kullanılarak sayısal çözüm gösterilmektedir. Devre denklemlerinden elde edilen bu denklemlerin çıkarılışı okuyucuya bırakılmıştır.

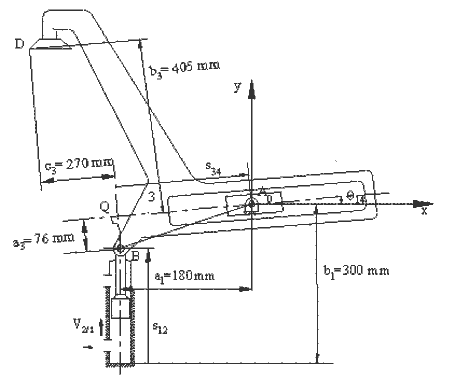
Konum analizi için gerekli olan denklemler:

s₃₄ = \displaystyle \sqrt{{{{{\left( {{{\text{b}}_{1}}-{{\text{s}}_{{12}}}} \right)}}^{2}}+{{\text{a}}_{1}}^{2}+{{\text{a}}_{3}}^{2}}}           γ = tan^-1(s₃₄/a₃)

ϕ = tan^-1[a₁/(b₁ − s₁₂)]          θ₁₄ = ϕ − γ

Şekilde θ₁₄ açısı gösterilmişdir. ϕ ve γ açıları bulunurken ATAN2() fonksiyonunun kullanılması doğru olacaktır. Karmaşık sayı ile D noktasının konum vektörü (A₀ merkezli ve x ekseni yatay olan bir referans koordinat ekseni kullanılmıştır):

r_D = (−s₃₄ − c₃ + ib₃)e^iθ₁₄

Reel sayıların kullanılması durumunda D noktası koordinatları (r_D = x_D + iy_D):

x_D = −(s₃₄ + c₃)cosθ₁₄ − b₃sinθ₁₄

y_D = −(s₃₄ + c₃)sinθ₁₄ + b₃cosθ₁₄

Hız analizi sırasında 2 uzvunun 180 mm/s hızla yukarıya doğru hareket ettiği kabul edilmiştir (v₁₂ = 180 mm/s). Hız denklemleri:

ω₁₄ = −(v₁₂/s₃₄)cosθ₁₄     ,    v₃₄ = \displaystyle {\dot{\text{s}}} ₃₄ = −(v₁₂/s₃₄)(a₃cosθ₁₄ + s₃₄sinθ₁₄)

D noktasının x ve y yönünde hız bileşenleri:

v_Dx = −y_Dω₁₄ − v₃₄cosθ₁₄     ,     v_Dy = x_Dω₁₄ − v₃₄sinθ₁₄

Yukarıda gösterilmiş olan bileşenler D noktasının hızını karmaşık sayılarla yazdığımızda (v_D = v_Dx + iv_Dy):

v_D = (−s₃₄ − c₃ + ib₃)iω₁₄e^iθ₁₄ − v₃₄e^iθ₁₄

Bu denklemin reel ve sanal kısımları ayrı, ayrı x ve y yönünde hız bileşenlerini verir.

2 pistonunun sabit hızda hareket ettiği düşünülerek ivme analizi yapıldığında elde edilen gerekli denklemler:

α₁₄ = (v₁₂/s₃₄²)(ω₁₄s₃₄sinθ₁₄ + v₃₄cosθ₁₄)

a₃₄ = \displaystyle {\ddot{\text{s}}} ₃₄ = (v₁₂/s₃₄²)[(a₃ω₁₄ − v₃₄)sinθ₁₄ − ω₁₄s₃₄cosθ₁₄]

D noktasının x ve y yönünde ivme bileşenleri:

a_Dx = −x_Dω₁₄² − y_Dα₁₄ + 2v₃₄ω₁₄sinθ₁₄ − a₃₄cosθ₁₄

a_Dy = −y_Dω₁₄² + x_Dα₁₄ + 2v₃₄ω₁₄cosθ₁₄ − a₃₄sinθ₁₄

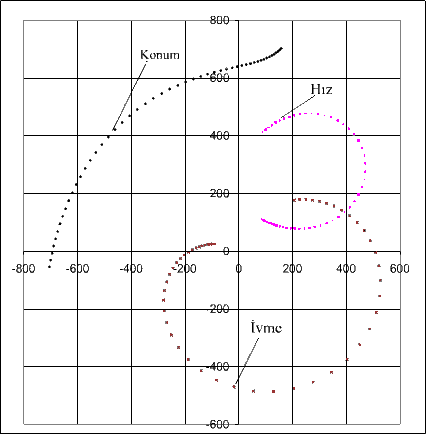
Denklemler Excel paket programı kullanılarak 60 mm < s < 500 mm aralığında her 10 mm için hesap edilerek şekilde gösterilen D noktasının konumu hızı ve ivmesi elde edilmiştir. Bu şekilde, konum hız ve ivme vektörleri (0, 0) noktasından ilgili eğri üzerinde bulunan noktaya giden vektördür. Yatay ve dikey eksenler konum için mm, hız için mm/s, ivme için ise mm/s² dir. Örneğin değer olarak s₁₂ = 60 mm iken:

s34 = 309.48 mm	θ14 = 39.33°	xD = −704.91 mm	yD = −54.03 mm
ω14 = −0.45 rad/s	v34 = −148.28 mm/s	vDx = 90.39 mm/s	vDy = 411.11 mm/s
α14 = −0.38 rad/s2	a34 = 0.34 mm/s2	aDx = 206.36 mm/s2	aDy = 176.38 mm/s2

olarak elde edilmiştir. s₁₂ = 200 mm iken ise:

s34= 219.49 mm	θ14 = 9.96°	xD = −552.14 mm	yD = 314.27 mm
ω14 = −0.81 rad/s	v34 = −92.51 mm/s	vDx = 344.96 mm/s	vDy = 461.97 mm/s
α14 = −0.46 rad/s2	a34 = 0.67 mm/s2	aDx = 528.39 mm/s2	aDy = −101.15 mm/s2

olarak elde edilmiştir.

Excel kütüğü için tıklayınız: –TransferMek.xls–

Aynı problemi grafik olarak çözmek istediğimizde

v_B4 = v_B3 + v_B4/3

vektör hız denkleminin çözümü gerekecektir. B₃ noktasının hızı, v_B3, B₂ noktasının hızına ve bu hız ise 2 uzvunun öteleme hızına eşittir (v_B3 = v_B2 = v₁₂). v_B4/3 bağıl hızının 3 ve 4 uzvu arasında bulunan kayar mafsal eksenine paralel olması gerekir. B₄ noktasının hızı, v_B4, 4 uzvu sabit bir eksen etrafında dönme yaptığından A₀B doğrusuna dik olmalıdır. İlk olarak v_B2 hız vektörünü k_v = 1 mm/(mm/s) ölçeği kullanarak mm şeklinde uzunluğa çevirdikten sonra bu uzunlukta 1 ve 2 uzvu arasında bulunan kayar çift eksenine paralel bir doğru olarak çizelim. Bu doğrunun başlangıç noktasından A₀B doğrusuna dik bir doğru ve uç noktasından 3 ve 4 uzvu arasında bulunan kayar çift eksenine paralel bir doğru çizelim. Bu iki doğrunun çakışma noktası bize v_B4 ve v_B4/3 hızlarının şiddetini verecektir (örneğin v_B4 = 176.8 mm/k_v = 176.8 mm/s). Bu hız poligonu çözüldükten sonra, 4 uzvunun açısal hızı: ω₁₄ = v_B4/|A₀B| = 176.77/239.54 = 0.74 rad/s olarak elde edilir. Bu açısal hız yönü v_B4 hız vektörüne göre saat yelkovanı yönünde olması gerekir. Ayrıca 3 ve 4 uzvu arasında kayar mafsaldan dolayı her hangi bir bağıl dönme olamayacağından ω₁₄ = ω₁₃ tür. Bu denklem çözüldükten sonra, D noktasının hızı için:

v_D = v_B3 + v_D/B3

hız denklemi yazılabilir. Bu denklemde v_D/B3 = ω₁₃|DB| = 0.738×551.41 = 406.9 mm/s dir ve v_D/B3 hız vektörü DB doğrusuna dik olmalıdır (ω₁₃ e göre DB doğrusu 90° saat yelkovanı yönünde döndürülecektir). Bu iki vektörün toplamı bize D noktasının hızını verir. Dikkat edilir ise, hız devre denklemine karşı gelen hız vektörü denklemi çözülmeden D noktasının hızını veren denklem çözülemez. Elde edilmiş olan sonuç, analitik olarak elde edilen sonuca sayısal olarak çok yakındır (Bunun nedeni her iki çözüm için bilgisayar kullanılmasındandır. Grafik çözüm pergel-cetvel ile yapılsa idi, fark görülür derecede olabilirdi).

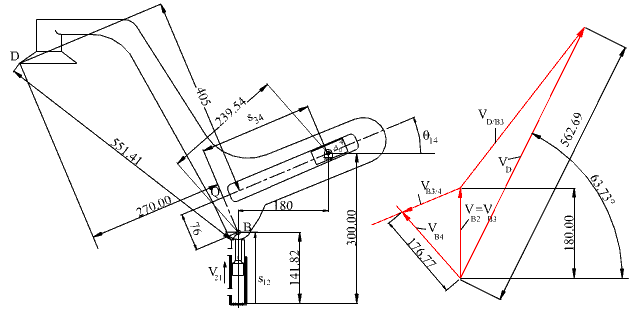
Bu şeklin AutoCad Kütüğü için tıklayınız: –TransferMek.dwg–

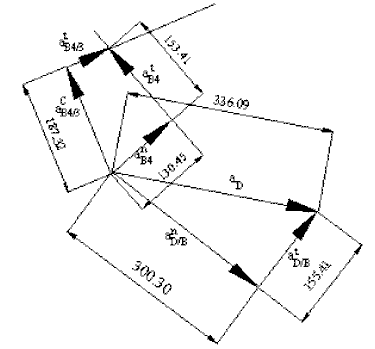
Aynı mekanizmanın grafik yöntemle ivme analizi için vektör ivme denklemi:

a^t_B4 + aⁿ_B4 = a_B3 + a^t_B4/3 + a^c_B4/2

olarak yazılabilir. B₄ noktasını ele aldığımızda a^t_B4 teğetsel ivmenin şiddeti α₁₄|BA₀| (α₁₄ bilinmiyor) ve yönü BA₀ olacaktır. aⁿ_B4 normal ivmenin ise şiddeti ω₁₄²|BA₀| = v_B4²/|BA₀| = 130.45 mm/s², yönü ise BA₀ yönünde ve A₀ a doğru olması gereklidir. B₃ ve B₂ noktaları daima çakışan noktalar olduğundan aynı hız ve ivmeye sahiptirler. Pistonun sabit bir hızla ötelediğini kabul eder isek: a_B2 = a_B3 = 0 dır. Teğetsel bağıl ivme a^t_B4/3 3 ve 4 uzvu arasında bulunan kayar mafsal ekseni yönünde bilinmeyen bir şiddetle oluşacaktır. a^c_B4/3 Coriolis ivmesine gelince, şiddeti 2ω₁₄v_B4/3 = 187.32 mm/s² dir, yönü ise v_B4/3 bağıl hız vektörünün ω₁₄ açısal hız vektörünün yönüne göre 90° döndürülmesi ile elde edilir. Bu ivme vektörleri bileşenlerini belirli bir ölçek kullanarak çizdiğimizde (k_a = 1 mm/(mm/s²) kullanılmıştır), a^t_B4 ve a^t_B4/3 ivmelerinin şiddeti bulunur (üstteki şekil).

D noktasının ivmesi için ise:

a_D = a_B3 + aⁿ_D/B + a^t_D/B

D noktasının yörüngesi bilinmediğinden dolayı, a_D ivmesini bileşkeleri ile yazmamız doğru olmayacaktır. a_B3 = 0 dır. aⁿ_D/B normal ivmesinin şiddeti ω₁₃²|BD| = 300.32 mm/s², yönü ise BD yönünde B ye doğru olacaktır. Bağıl teğetsel ivme, a^t_D/B nin şiddeti α₁₃|BD| dir. α₁₃ = α₁₄ = a^t_B4/|BA₀| = 0.640 rad/s² olduğundan a^t_D/B şiddeti 153.41 mm/s² bulunur ve yönü DB doğrusunun α₁₃ yönünde 90° döndürülmesi ile elde edilir. Yönleri ve şiddetleri bilinen bu vektörlerin toplamı D noktasının ivmesini şiddet ve yön olarak verecektir.