Engineering economy is “a collection of techniques that simplify comparisons of alternatives on an economic basis”
Sensitivity analysis has different implications, depends on the person evaluating the data and it is not within the scope of this course.
Interest Rate and Rate of Return
Interest: The difference between an ending amount of money and beginning amount. Another description is the money paid for the use of the borrowed money.
Interest paid: money borrowed and repaid a larger amount over time
Interest earned: money invested/lent and a larger amount is earned in time.
Interest = Amount owned now – Principal
Interest rate: The representation of the interest paid over a period of time.
Interest rate = (Interest accured per time unit/Principal)x100%
Interest period: The time unit of the interest rate. Commonly per year. If not indicated, assume
it is yearly
Basic Terminology and Fundamental Concepts
Earning power of money: the ability of making profit using the money to buy an item which
will lead to higher gain.
Time value of money: The change in the amount of money over a given time period is called the
“time value of money”. This is the most important concept in engineering economics. Money has
a time value, because it can earn more money over time and its purchasing power changes over time.
Earning power: ability of making profit/
money makes money
Inflation: the value of money goes down
Economic equivalence: different sums of money
at different times would be equal in “economic value”.
Evaluation criteria: In economic analysis “financial units” (Dollar, TL or any other currency) are generally used as the tangible basis for evaluation. For selecting the economically best alternative the alternative with the “lowest overall cost” or “highest overall net income” can be identified.
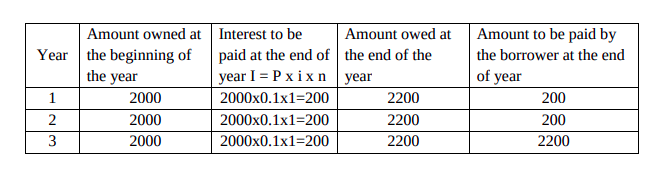
Simple and Compound Interest
Simple Interest (Basit faiz):

It is possible that a provision is made such that the interest earned is paid at the end of each
interest period. This can be explained as follows:
Cash flow (nakit akisi): It is the movement of money into and out of an account, business etc.
Cash flow is the estimated inflows (revenues/incomes) & outflows (costs) of money.
Cash inflows: Receipts, revenues, incomes, savings, salvage value etc. They are designated with a + sign.
Cash outflows: Costs (e.g. first cost, operating cost, maintenance cost etc.), taxes,
disbursements, expenses. They are designated with a – sign.
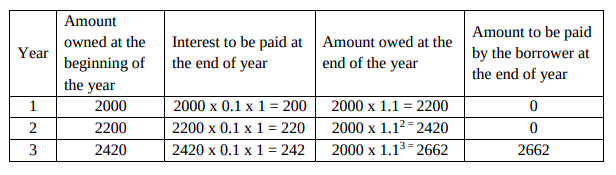
Compound Interest (Bileşik faiz):

Ex:
Single Payment Compound-amount Factor: finding the amount due at the end of the period by multiplying the principal by a factor
(1+i)n(1+i)^n
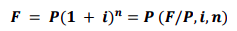
where,
- F = Value/amount of money accumulated after n periods of time. Also called Future Worth (FW)
or Future Value (FV). (Paranin gelecek degeri). Units: Dollars, Turkish Lira, Euro etc. - P = Principal amount, Value of money at the present. Also designated as present worth (PW),
present value (PV). (Paranin bugunki degeri). Units: Dollars, Turkish Lira, Euro etc.
7 - i = Interest rate/ rate of return per time period, units: % per year, % per month, % per day etc.
- n = Number of interest periods. Units: years, months, days, etc.
(X/Y, i, n) The letter X represents what is sought, while the letter Y represents what is given.
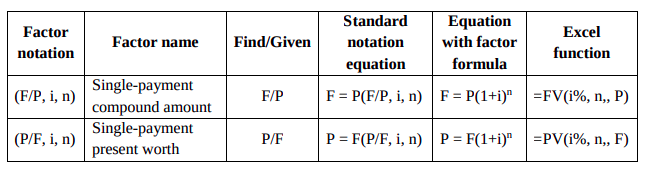
Single Payment Present Worth Factor (Tek ödemeli şimdiki değer faktörü)
Reverse the situation to determine P value for stated amount of F that occurs n
periods in the future
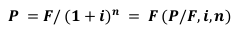
Equal Payment Series Compound Amount Factor (Eşit seri ödemeli akümüle değer
faktörü)
- a series of equal payments occurring at the end of each succeeding annual interest period is encountered.
A = Series of consecutive, equal, end-of-period amounts of money.
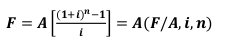
Equal Payment Series Sinking Fund Factor (Eşit seri ödemeli birikim fonu faktörü)
In order to find out the necessary year end payments A, in order to accumulate a future amount
F, the reverse formula is used.
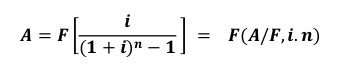
Equal Payment Series Capital Recovery Factor (Eşit seri ödemeli kapitali kurtarma faktörü)
Substitute F by P(1+i) n in equal series payment sinking fund factor.

Equal Payment Series Present Worth Factor (Eşit seri ödemeli bugünki değer faktörü)
1/capital recovery factor.
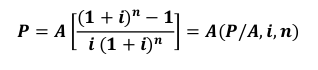
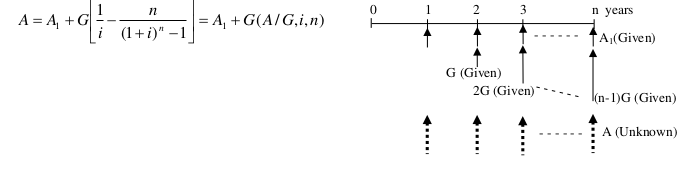
Uniform Gradient Series Factor (Düzenli artan/eksilen ödemeler faktörü):
In some cases, annual payments don’t occur in equal payment series. It is possible to have a uniformly increasing series, such as A 1 , A 1 +G, A 1 +2G, A 1 +3G, …, A 1 +(n-1)G.
A = A_1 + A_2 where,

Interest Factors
Single-payment compound-amount factor. (Tek ödemeli akümüle değer faktörü)

Single-payment present worth factor. (Tek ödemeli güncel değer faktörü)
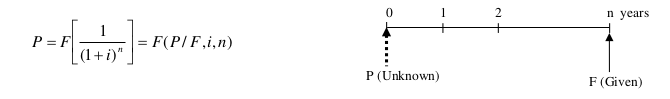
Equal-payment series compound-amount factor. (Eşit seri ödemeli akümüle değer faktörü)
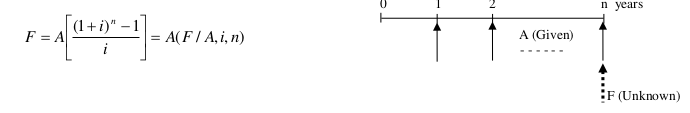
Equal-payment series sinking-fund factor. (Eşit seri ödemeli birikim fonu faktörü)
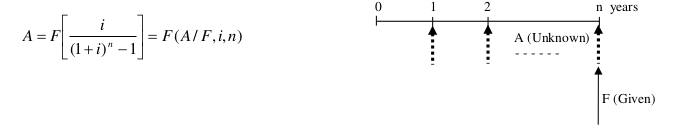
Equal-payment series capital-recovery factor. (Eşit seri ödemeli kapital geri kazanım faktörü)

Equal-payment series present worth factor. (Eşit seri ödemeli güncel değer faktörü)

Uniform gradient series factor. (Düzenli artan/eksilen seri ödemeler faktörü)
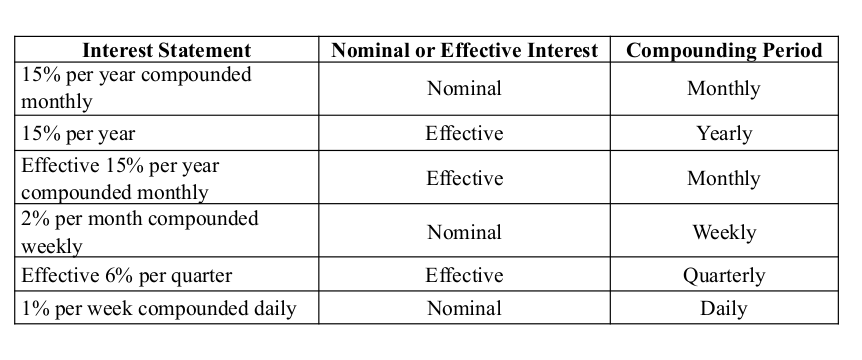
NOMINAL AND EFFECTIVE INTEREST
- less than 1 year
- When an interest rate is expressed over a period of time shorter than a year, such as 1% per month
- Nominal interest rate is not a correct or actual rate. So, it should to convert effective rates
Nominal interest rate
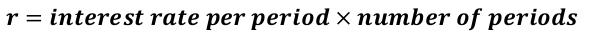
Effective interest rate

COMPARISON OF ALTERNATIVES
Alternatives: An alternative is a single, independent solution for a given situation.
- First cost (purchase/investment cost),
- Expected useful/service life,
- Annual maintenance and operating costs (yearly cost of maintaining assets),
- Book value (expected resale value at any time, net worth of an asset that is recorded on
the balance sheet), - Salvage value (expected resale value at the end of its service life), and
- Interest rate.
Alternative selection: Alternatives
Tools to compare attractiveness of possible investment options
- The Present Worth method
- The Annual Equivalent method
- The Rate of Return method
Minimum Attractive Rate of Return (MARR)
In order to compare attractiveness of alternative investments, a reasonable rate of return should
be stated and attractiveness of options should be determined using this value. This reasonable
rate is MARR.
ROR >= MARR -> project is acceptable
ROR < MARR -> project is unacceptable
MARR
MARR is higher than the rate expected from a bank or some safe investment which involves
minimal investment risk.
- If MARR selected is too high, some attractive options may be rejected.
- If MARR selected is too low, some options may result in economic loss.
Present Worth method(PW)
Present equivalent of receipts and disbursements are compared at the same point in time
- Compare the present worth of each alternative (to calculate PW, MARR should be
assumed. Select MARR carefully as PW is sensitive to changes in MARR). - “n” for each alternative should be considered carefully. To make a valid PW comparison
same periods should be used for each alternative.
(P/A,x%,n)
Annual Equivalent method(AE)
PWAPWB=AEAAEB
{PW_A\over PW_B} = {AE_A \over AE_B}
Procedure is the same whether the service lives are equal or not.
(A/P,x%,n)
Rate Of Return
One of the obvious differences between RoR and the others (PW, AE) is that: No interest rate
has to be known in order to decide the RoR