Shapley Values: Ensuring Equity in Game Theory
Shapley Values are a fundamental concept in game theory, offering an equitable mechanism for dividing the total gains of a collaborative game among its participants. Introduced by Lloyd Shapley in 1953, this idea centres on the principle that each player should receive compensation commensurate with their marginal contribution to the game’s overall outcome.
In essence, Shapley Values provide a framework to address a critical question: What is the significance of each player’s role in the collective cooperation, and consequently, what portion of the rewards can each player expect?
To delve into the mathematical intricacies, let’s embark on a practical example:
Mathematical Underpinnings of Shapley Values
Consider a cooperative game involving four individuals: Emily, Frank, Grace, and Henry. These individuals have collectively decided to unite and engage in the game as a coalition. Their combined efforts yield a total winnings of $1000.
At this juncture, the players face the task of fairly distributing the $1000 prize money amongst themselves. To ascertain each player’s portion, we must calculate their individual Shapley Values, quantifying their contribution to the collective prize.
To accurately determine each player’s share of the winnings, calculating their individual Shapley Values becomes imperative — these values gauge their impact on the total prize money.
To effectively compute the Shapley Values, we also need to know how much each player would have earned had they participated as individuals (assuming we possess this information). Here are the individual amounts that Emily, Frank, Grace, and Henry would have respectively earned:
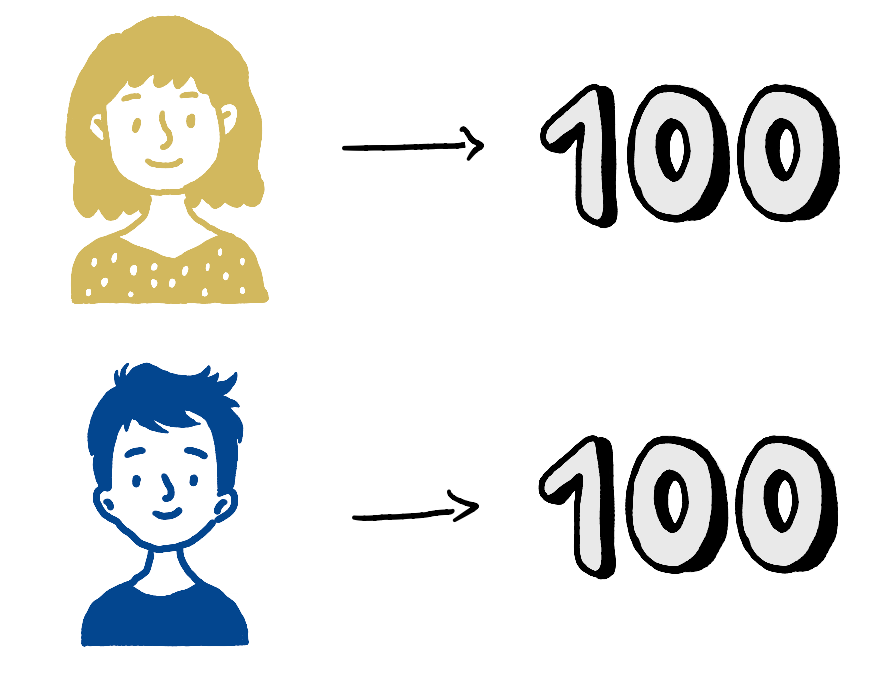
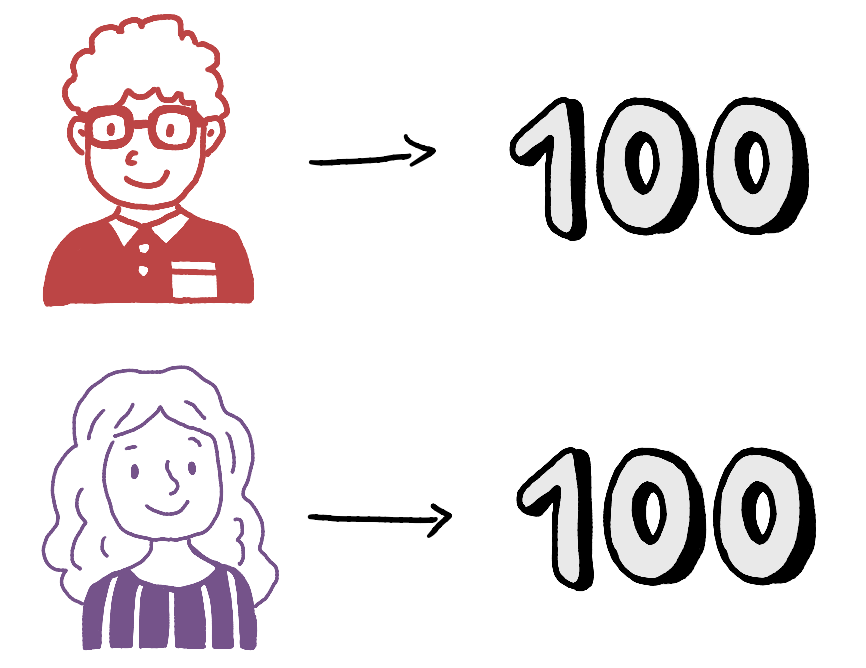
Although it might seem that the individual points accumulated by each player reflect their marginal inputs into the collective prize, this presumption isn’t always accurate. This is due to the potential variation when players join forces in pairs or trios, leading to differing contributions and varying prize earnings. To address this, we must factor in the earnings each pair of players would have attained if they collaborated and established coalitions of two.


Likewise, there’s the possibility of creating coalitions of three, yielding these respective earnings:

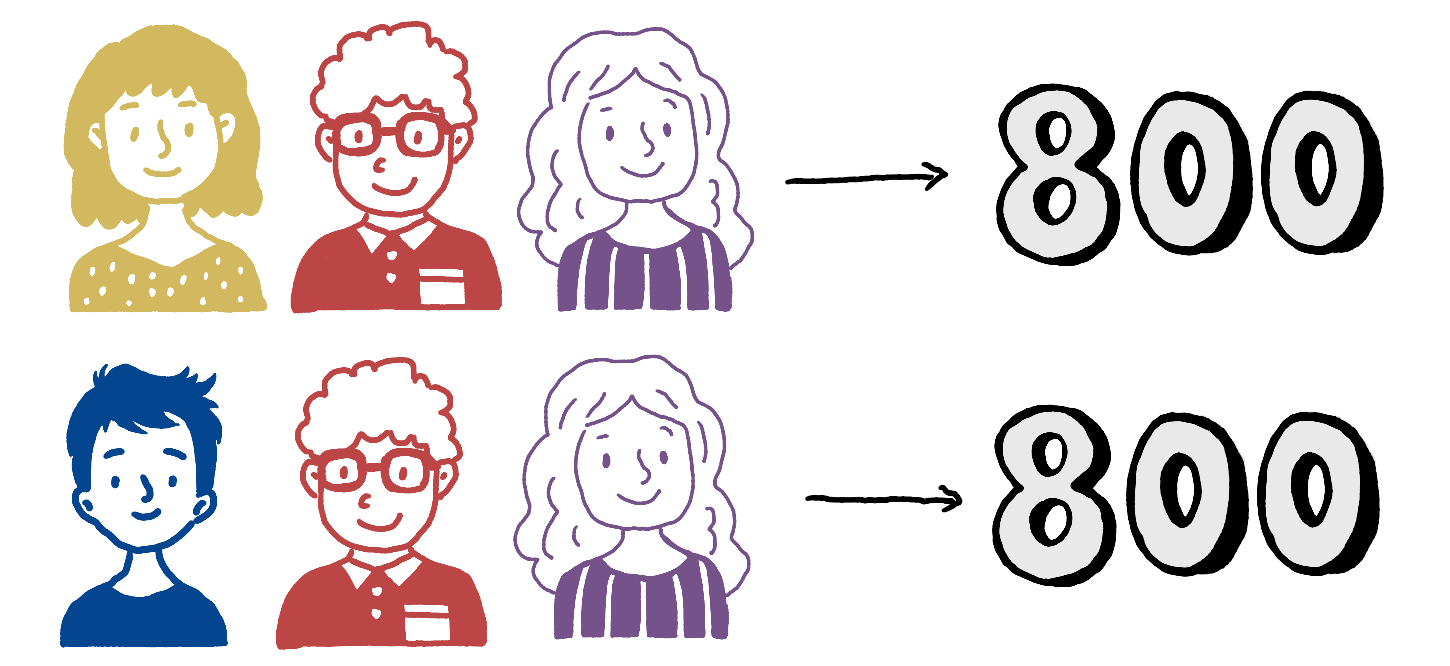
Indeed, if no participants engage, the outcome would result in zero winnings, corresponding to a coalition of size 0.
Given the individual and combined contributions, we are now poised to calculate the Shapley Value for each player, a pivotal step in establishing their equitable slice of the prize money. Let’s commence the process by computing Emily’s marginal contribution, following these steps:
Step 1: Identify the coalitions formed that do not include Emily.
Step 2: Determine the quantity of coalitions generated for each coalition size.
In this context, due to the limited number of players (four), tallying the coalitions of varying sizes is relatively straightforward. Nevertheless, as games expand in scale, involving, for instance, 100 players, this computation becomes notably intricate. A saving grace emerges in the form of the combination formula from probability theory, which aids in calculating these figures systematically.
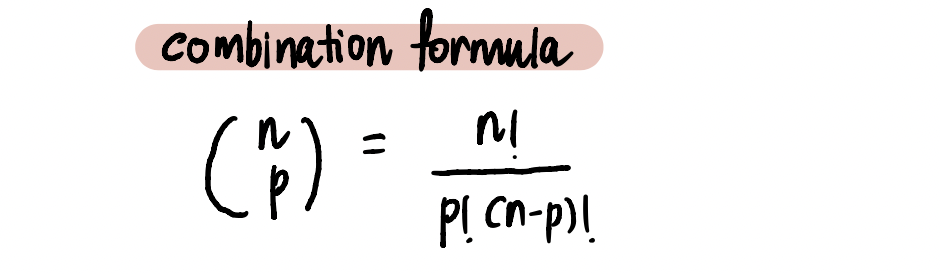
As an illustration, if our objective involves determining the count of coalitions sized 2 that omit Emily, the approach entails selecting 2 participants from the remaining trio (Frank, Grace, and Henry). This procedure can be conceptualized through the combination process.
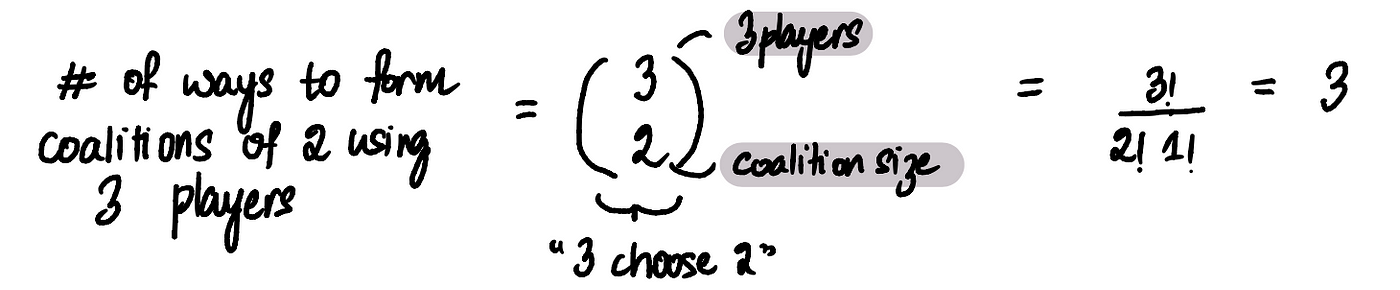
Let’s begin by calculating the average marginal contribution for coalitions of size 2.
To initiate this process, we need to compute the disparity in prize money when transitioning from a coalition without Emily to one that includes her.
Subsequently, we aggregate all these disparities and divide the cumulative sum by the total count of coalitions sized 2. This outcome yields the average marginal contribution for coalitions of size 2.
As an illustrative example, let’s examine the initial coalition of size 2, comprising Frank and Grace. Observing the scenario, it’s evident that they would have collectively secured $400. Now, let’s incorporate Emily into this coalition. With Emily’s inclusion, the winnings escalate to $700. The disparity between the two scenarios is:
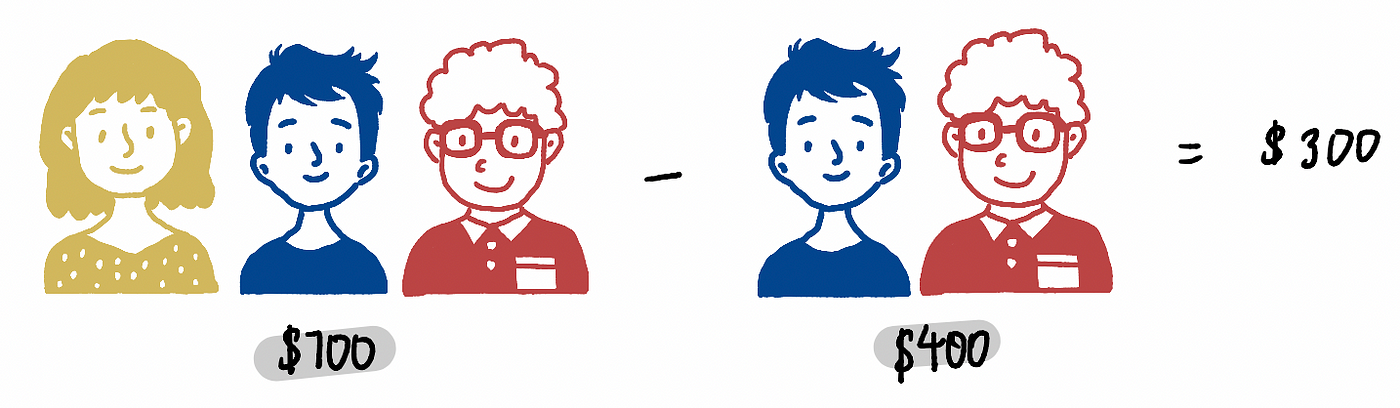
Hence, it’s apparent that integrating Emily into this coalition boosts its value by $300, which constitutes Emily’s marginal contribution. Subsequently, we perform the division by taking the cumulative sum of these marginal contributions and dividing it by the overall count of coalitions sized 3 (using the formula stipulated in Step 2):
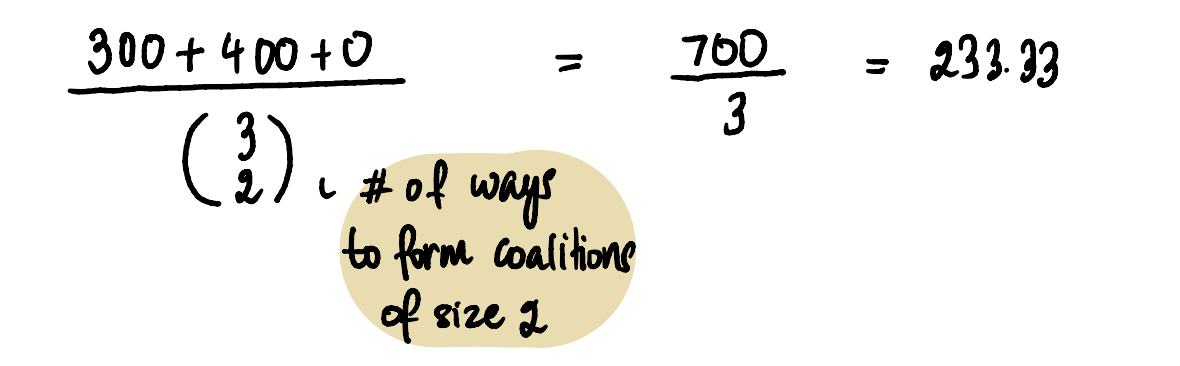
This can be construed as follows: on average, Emily provides an incremental contribution of $233.33 when incorporated into coalitions of size 2.
We proceed similarly for coalitions of size 3. Given that there exists only one coalition of size 3, we compute the variation in prize money when Emily becomes a part of this coalition:
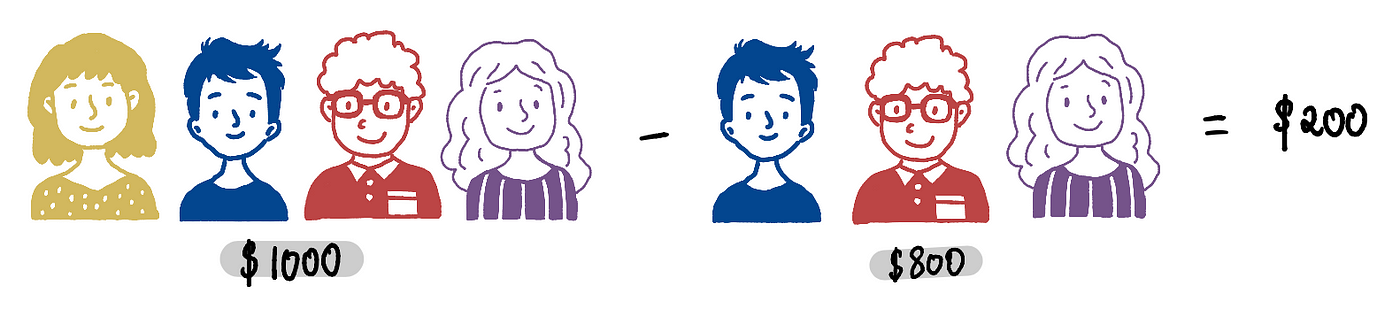
And then divide this by the number of coalitions of size 3.
And for coalitions of size 1:
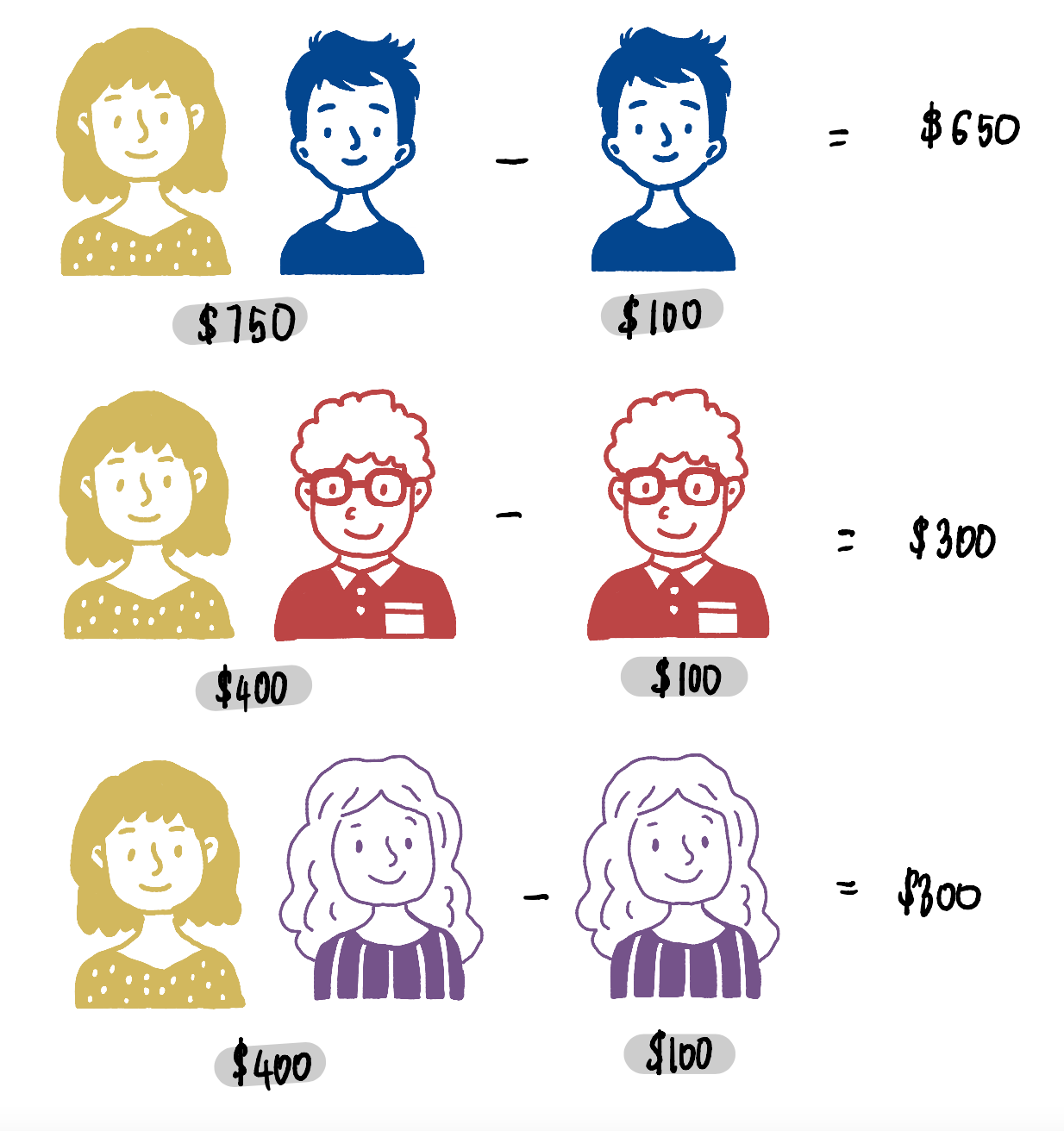
And coalitions of size 0:
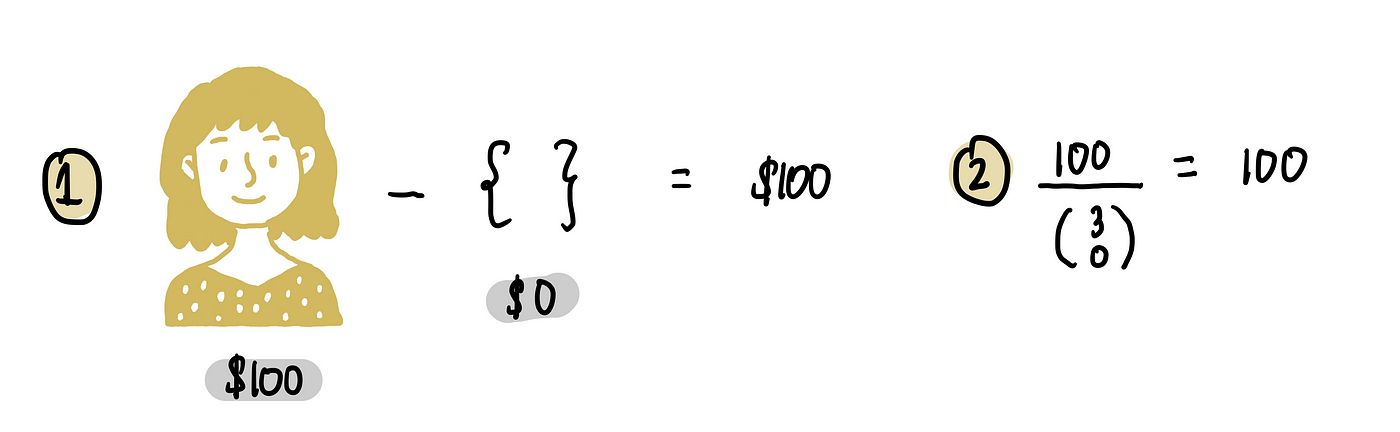
Step 4: Determine Emily’s Shapley Value
To derive Emily’s Shapley Value, we aggregate the average marginal contributions originating from the diverse coalition sizes. This cumulative sum is then divided by the count of distinct coalition sizes, excluding Emily.
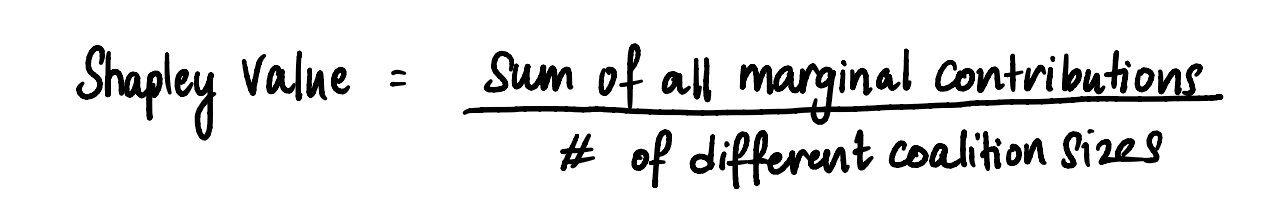
In the analysis conducted, it’s evident that four coalition sizes (0, 1, 2, and 3) are observed in scenarios excluding Emily. Therefore, Emily’s contribution to the $1000 prize money amounted to $237.5. Adding these values together, we observe that $237.5 + $237.5 + $245.8333 + $279.1667 equals $1000, aligning perfectly with the total prize money won. These Shapley Values indeed represent an equitable distribution of each player’s marginal contributions, ultimately determining the portion of money allocated to each participant.

And thus, we conclude our exploration of Shapley Values with a succinct understanding. In recent times, these values have gained prominence in the realm of machine learning, particularly for interpreting models, especially those that present challenges in terms of interpretability.
