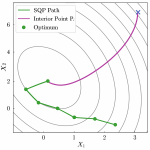
Optimization plays a fundamental role in the design and performance enhancement of wireless communication systems. Many classical problems, such as power control, beamforming, and resource allocation, can be formulated as convex optimization problems, leading to efficient and globally optimal solutions within polynomial time using well-established methods like interior-point algorithms.
However, real-world wireless systems often involve nonconvex challenges due to interference management, hardware limitations, and the nonlinearity of practical objective functions such as sum-rate maximization or energy efficiency. In these nonconvex scenarios, specialized algorithms such as Sequential Quadratic Programming (SQP), Successive Convex Approximation (SCA), and Lagrangian methods are employed to find high-quality local optima.
Although convex methods are preferred for their optimum solutions and fast convergence, nonconvex approaches are essential for handling the complex, highly coupled nature of wireless networks. As wireless technologies evolve towards massive MIMO, mmWave, and integrated sensing and communication (ISAC), knowing both convex and nonconvex optimization techniques becomes crucial for achieving high performance and reliability in these systems.
Convex vs Nonconvex Optimization
| Aspect | Convex Optimization | Nonconvex Optimization |
|---|---|---|
| Problem structure | Objective and constraints are convex. | Objective or constraints are nonconvex. |
| Examples |
– Power allocation (water-filling) – Beamforming with SINR constraints (under certain conditions) |
– Sum rate maximization – Energy efficiency optimization |
| Solvers | Efficient (e.g., CVX, SCS, MOSEK) | Heuristic (e.g., SCA, MM, Deep Learning, Global optimization) |
| Global optimum? | Yes (guaranteed) | No (local optima usually found) |
| Speed | Fast, polynomial-time algorithms | Slower, depending on method and initialization |
| Difficulty | Easier to model, solve, and analyze. | Harder: often require approximations, relaxations, iterations |
| Common Techniques |
– Lagrangian duality – KKT conditions – Interior point methods |
– Successive Convex Approximation (SCA) – Semidefinite Relaxation (SDR) – Stochastic optimization – Reinforcement learning |
| Use in Wireless Systems |
– Beamforming – Power control – Resource allocation |
– MIMO sum rate – Energy-harvesting systems – Intelligent Reflecting Surfaces (IRS) design |
Some Nonconvex Optimization Methods
| Method | Idea | Pros | Cons |
|---|---|---|---|
| SCA (Successive Convex Approx.) | Linearize around the current point, solve convexly | Simple, flexible | May converge slowly |
| SDR (Semidefinite Relaxation) | Relax rank constraints in SDP form | Global optima for relaxed problem | May not recover rank-1 solution |
| ADMM (Alternating Direction Method of Multipliers) | Split variables and solve alternately | Good for decentralized systems | Slow convergence sometimes |
| Deep Learning | Data-driven mapping from inputs to outputs | Super fast inference | No guarantee on optimality |
| SQP (Sequential Quadratic Programming) | Solve a sequence of quadratic approximations of the problem | Fast local convergence. Handles nonconvexity moderately well | Needs good initialization. May get stuck in poor local minima |
Comparison of Interior Point Method (IPM) and Sequential Quadratic Programming (SQP)
| Feature | Interior Point Method (IPM) | Sequential Quadratic Programming (SQP) |
|---|---|---|
| Idea | Solve constrained problems by moving through the interior of the feasible region using a barrier function. | Solve by approximating the problem locally as a quadratic program (QP). |
| How it works | Adds a penalty (log-barrier) for constraint violation; optimizes a “smoothed” version of the problem. | At each step, solve a quadratic approximation of the Lagrangian with linearized constraints. |
| Handling Constraints | Implicit: constraints are incorporated into the objective using barrier functions. | Explicit: constraints are enforced at every step in the QP subproblem. |
| Steps per Iteration | 1. Solve a modified Newton step for the barrier problem. 2. Decrease barrier weight. |
1. Build QP. 2. Solve QP. 3. Line search for improvement. |
| Complexity per Iteration | High — solving a large, dense linear system. | Moderate — solving a QP (still needs a solver but often cheaper). |
| Global Convergence | Good, especially for convex problems. | Requires good initialization. Might fail on badly nonconvex problems. |
| Speed of Convergence | Superlinear near solution (for convex). | Superlinear (very fast near the solution). |
| Suitability | Works very well for large-scale convex optimization. | Better for small to medium-scale, highly accurate solutions. |
| Pros | – Good at exploring feasible regions. – No need for feasible starting point. – Great for convex problems. |
– Very fast local convergence. – Good for nonconvex problems if properly initialized. – Explicit constraint handling. |
| Cons | – Can be slow if the barrier weight is not managed well. – Struggles with highly nonconvex problems. |
– Sensitive to initialization. – May converge to local minima. – Each QP solve can be costly for very large problems. |
Note: The tables are generated with the help of generative AI (ChatGPT).
I have listed below some related research articles that can be read to get insight into the optimization of wireless communication systems. This list will be updated as I come across new articles.
- Shen, Kaiming, and Wei Yu. “Fractional programming for communication systems—Part I: Power control and beamforming.” IEEE Transactions on Signal Processing 66.10 (2018): 2616-2630.
- Shen, Kaiming, and Wei Yu. “Fractional programming for communication systems—Part II: Uplink scheduling via matching.” IEEE Transactions on Signal Processing 66.10 (2018): 2631-2644.
- Scutari, Gesualdo, Francisco Facchinei, and Lorenzo Lampariello. “Parallel and distributed methods for constrained nonconvex optimization—Part I: Theory.” IEEE Transactions on Signal Processing 65.8 (2016): 1929-1944.
- Scutari, Gesualdo, et al. “Parallel and distributed methods for constrained nonconvex optimization-part ii: Applications in communications and machine learning.” IEEE Transactions on Signal Processing 65.8 (2016): 1945-1960.
- Khan, Ahmad Ali, and Raviraj S. Adve. “Percentile Optimization in Wireless Networks—Part I: Power Control for Max-Min-Rate to Sum-Rate Maximization (and Everything in Between).” IEEE Transactions on Signal Processing (2024).
- Khan, Ahmad Ali, and Raviraj S. Adve. “Percentile Optimization in Wireless Networks—Part II: Beamforming for Cell-Edge Throughput Maximization.” IEEE Transactions on Signal Processing (2024).
- Björnson, Emil, Mats Bengtsson, and Björn Ottersten. “Optimal multiuser transmit beamforming: A difficult problem with a simple solution structure [lecture notes].” IEEE Signal Processing Magazine 31.4 (2014): 142-148.
- Elbir, Ahmet M., et al. “Twenty-five years of advances in beamforming: From convex and nonconvex optimization to learning techniques.” IEEE Signal Processing Magazine 40.4 (2023): 118-131.
- Razaviyayn, Meisam, et al. “Nonconvex min-max optimization: Applications, challenges, and recent theoretical advances.” IEEE Signal Processing Magazine 37.5 (2020): 55-66.
- Liu, Ya-Feng, et al. “A survey of recent advances in optimization methods for wireless communications.” IEEE Journal on Selected Areas in Communications (2024).
- Lang, Hans-Dieter, Alon Ludwig, and Costas D. Sarris. “Convex optimization of wireless power transfer systems with multiple transmitters.” IEEE Transactions on Antennas and Propagation 62.9 (2014): 4623-4636.
- Luo, Zhi-Quan, and Wei Yu. “An introduction to convex optimization for communications and signal processing.” IEEE Journal on selected areas in communications 24.8 (2006): 1426-1438.
- Xu, Qinyi, et al. “Waveforming: An overview with beamforming.” IEEE Communications Surveys & Tutorials 20.1 (2017): 132-149.
- Temiz, Murat, Emad Alsusa, and Mohammed W. Baidas. “Optimized precoders for massive MIMO OFDM dual radar-communication systems.” IEEE Transactions on Communications 69.7 (2021): 4781-4794.
- Gershman, Alex B., et al. “Convex optimization-based beamforming.” IEEE Signal Processing Magazine 27.3 (2010): 62-75.
- Chiang, Mung. “Nonconvex optimization for communication networks.” Advances in Applied Mathematics and Global Optimization: In Honor of Gilbert Strang (2009): 137-196.
- Danilova, Marina, et al. “Recent theoretical advances in non-convex optimization.” High-Dimensional Optimization and Probability: With a View Towards Data Science. Cham: Springer International Publishing, 2022. 79-163.
- Nemirovski, Arkadi S., and Michael J. Todd. “Interior-point methods for optimization.” Acta Numerica 17 (2008): 191-234.
- Gill, Philip E., Walter Murray, and Michael A. Saunders. “SNOPT: An SQP algorithm for large-scale constrained optimization.” SIAM review 47.1 (2005): 99-131.
A student-contributed electronic textbook covering a variety of topics on process optimization: https://optimization.cbe.cornell.edu/index.php?title=Main_Page
Let me know below in the comment section below if you want me to add any articles to this list or if you have any suggestions regarding this post.