6.1 Basit Dişli Zincirleri

Eğer dişli çiftini oluşturan kinematik elemanları taşıyan uzuvlar aynı zamanda sabit uzva bir döner çift ile bağlı ise, bu tür dişli zincirlerine basit dişli zincir denecektir. Tek bir dişli çifte sahip basit dişli zincir Şekilde görülmektedir. Iki uzuv arasında anlık çakışan P temas noktasında, iki uzuv arasında kayma olmayıp sadece yuvarlanma olduğundan, bağıl hız sıfırdır. Bu durumda P₂ ve P₃ noktalarının hızları aynı olacaktır. Hız oranı olarak N₂₃ ü:

\displaystyle {{\text{N}}_{{23}}}=\frac{{{\text{ω}_{{13}}}}}{{{\text{ω}_{{12}}}}}=\frac{{{{\text{n}}_{{13}}}}}{{{{\text{n}}_{{12}}}}}

tanımlayalım. Burada n_1j devir/dakika cinsinden j uzvunun hızıdır. P noktasının hızı:

\displaystyle {\text{v}_{{{\text{P}_{3}}}}}~={\text{v}_{{{\text{P}_{2}}}}}={\text{ω}_{{13}}}{\text{r}_{3}}={\text{ω}_{{12}}}{\text{r}_{2}}

dır. Bu durumda:

\displaystyle {{\text{N}}_{{23}}}=\frac{{{{\text{ω}}_{{13}}}}}{{{{\text{ω}}_{{12}}}}}=\frac{{{{\text{n}}_{{13}}}}}{{{{\text{n}}_{{12}}}}}=\frac{{{\text{r}_{2}}}}{{{\text{r}_{3}}}}=\frac{{{\text{d}_{2}}}}{{{\text{d}_{3}}}}

bu denklemde d_i ve r_i i uzvunda dişli bölüm dairesi çapı ve yarı çapıdır.

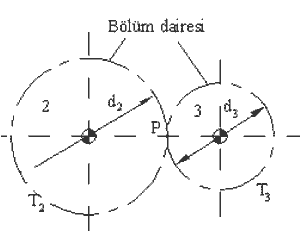
Dişli teorisine göre, dişli çifti oluşturan kinematik elemanların birbirleri ile uyumlu olabilmeleri için, her bir dişin bölüm dairesi üzerinde kapsadığı yay uzunluğu aynı olmalıdır. Eğer çevredeki diş sayısı \displaystyle T_{i} ise bu yay uzunluğu m = πd_i/T_i  (sabit), veya T_i/d_i = π/C = P_D ( sabit). Birbirleri ile çalışan iki dişli için bu oran aynı olması gerektiğinden:

\displaystyle \frac{{{\text{T}_{3}}}}{{{\text{d}_{3}}}}=\frac{{{\text{T}_{2}}}}{{{\text{d}_{2}}}}

olması gerekir. Bunun sağlanması için dişli çift oluşturacak dişlilerin belirli m veya P_D değerleri ile üretilmesi gerekir. Avrupada genellikle dişliler değişik m – modül (birimi mm dir) değerlerinde, İngilizce konuşulan ülkelerde ise genellikle dişliler değişik P_D – çap adımı (birimi 1/inch dir) değerlerinde üretilir ve bu değerlerin standardları bulunmaktadır.

Hız oranını dişli çift ile birleştirilen iki uzuv aynı yönde dönüyor ise pozitif, birbirlerine göre ters yönde dönüyor ise negatif olarak tanımlayalım. yukarıdaki şekilde görüldüğü gibi P temas noktası döner mafsal eksenleri arasında ise (buna dış dişli çift diyeceğiz), uzuvlar ters yönde; aşağıdaki şekilde görüldüğü gibi P temas noktası döner mafsal eksenleri dışında ise (buna iç dişli çift diyeceğiz), uzuvlar aynı yönde döneceklerdir.

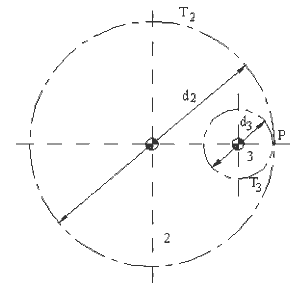
Basit dişli zincirde hız oranı:

\displaystyle {\text{N}_{{23}}}=\frac{{{\text{ω}_{{13}}}}}{{{\text{ω}_{{12}}}}}=\frac{{{\text{n}_{{13}}}}}{{{\text{n}_{{12}}}}}=\pm \frac{{{\text{r}_{2}}}}{{{\text{r}_{3}}}}=\pm \frac{{{\text{d}_{2}}}}{{{\text{d}_{3}}}}=\pm \frac{{{\text{T}_{2}}}}{{{\text{T}_{3}}}}={\text{R}_{{23}}} = Dişli Oranı

dır. Bu denklemde işaret dişli çift iç dişli çift ise artı (+), dış dişli çift ise eksi (−) dir.

Görüldüğü gibi, basit dişli zincirler için hız oranı (N_ij) ile dişli oranı (R_ij) birbirlerine eşittir.

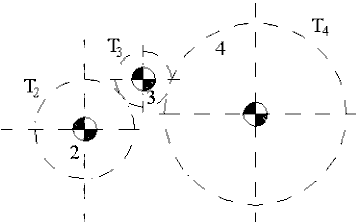
Aşağıdaki şekilde görülen basit dişli zinciri ele alalım. 2 uzvu 3 uzvu ile ve 3 uzvu aynı kinematik elemanı kullanarak 4 uzvu ile dişli çift oluşturmuştur. Dişli oranını her bir dişli çift için yazdığımızda:

\displaystyle {\text{R}_{{23}}}=\frac{{{\text{n}_{{13}}}}}{{{\text{n}_{{12}}}}}=-\frac{{{\text{T}_{2}}}}{{{\text{T}_{3}}}}\text{ , }{\text{R}_{{34}}}=\frac{{{\text{n}_{{14}}}}}{{{\text{n}_{{13}}}}}=-\frac{{{\text{T}_{3}}}}{{{\text{T}_{4}}}}

ve

\displaystyle {\text{R}_{{24}}}=\frac{{{\text{n}_{{14}}}}}{{{\text{n}_{{12}}}}}=\frac{{{\text{n}_{{13}}}}}{{{\text{n}_{{12}}}}}\frac{{{\text{n}_{{14}}}}}{{{\text{n}_{{13}}}}}={\text{R}_{{23}}}{\text{R}_{{34}}}=\left( {-\frac{{{\text{T}_{2}}}}{{{\text{T}_{3}}}}} \right)\left( {-\frac{{{\text{T}_{3}}}}{{{\text{T}_{4}}}}} \right)=\frac{{{\text{T}_{2}}}}{{{\text{T}_{4}}}}

olacaktır. Denklemden görüldüğü gibi, 3 uzvu üzerinde bulunan diş sayısı hız oranı şiddetini etkilememekte, ancak iki dış dişli olduğundan oran artı olmaktadır. Bu ara dişliler genellikle avare dişli olarak adlandırılırlar. Öncelikle hız yönünü istenilen yöne değiştirmek için veya aralarında büyük mesafe bulunan iki milin belirli bir hız oranı ile birbirine bağlanması gerektiğinde dişli çapını küçük değerlerde tutmak için kullanılır.

Birleşik basit dişli zincir sistemlerinde ise, her bir uzuv üzerinde dişli çift oluşturan iki değişik çapta dişli bulunmaktadır. Aşağıdaki şekilde bir örnek görülmektedir. Bu tür zincirlerde bazı uzuvlar avare dişlide olabilir. Tüm zincirin hız oranını belirlemek için her bir dişli çift teker teker ele alınabilir:

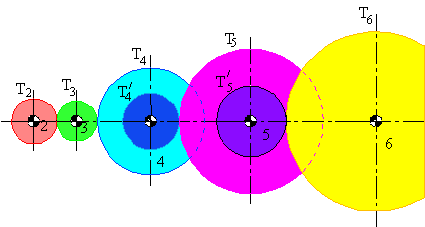
Dişli çift ile bağlanan uzuvlar için:

\displaystyle {\text{R}_{{23}}}=\frac{{{\text{n}_{{13}}}}}{{{\text{n}_{{12}}}}}=-\frac{{{\text{T}_{2}}}}{{{\text{T}_{3}}}}\text{   ,   }{\text{R}_{{34}}}=\frac{{{\text{n}_{{14}}}}}{{{\text{n}_{{13}}}}}=-\frac{{{\text{T}_{3}}}}{{{\text{T}_{4}}}}\text{   ,   }{\text{R}_{{45}}}=\frac{{{\text{n}_{{15}}}}}{{{\text{n}_{{14}}}}}=-\frac{{{\text{T}_{4}}^{\prime }}}{{{\text{T}_{5}}}}\text{   ,   }{\text{R}_{{56}}}=\frac{{{\text{n}_{{16}}}}}{{{\text{n}_{{15}}}}}=-\frac{{{\text{T}_{5}}^{\prime }}}{{{\text{T}_{6}}}}

dir. Bu durumda denklemlerin sağ tarafları ile sol taraflarının çarpımından:

\displaystyle {\text{R}_{{26}}}=\frac{{{\text{n}_{{16}}}}}{{{\text{n}_{{12}}}}}=\frac{{{\text{n}_{{13}}}}}{{{\text{n}_{{12}}}}}\frac{{{\text{n}_{{14}}}}}{{{\text{n}_{{13}}}}}\frac{{{\text{n}_{{15}}}}}{{{\text{n}_{{14}}}}}\frac{{{\text{n}_{{16}}}}}{{{\text{n}_{{15}}}}}={\text{R}_{{23}}}{\text{R}_{{34}}}{\text{R}_{{45}}}{\text{R}_{{56}}}={{\left( {-1} \right)}^{4}}\frac{{{\text{T}_{2}}{\text{T}_{3}}{\text{T}_{4}}^{\prime }{\text{T}_{5}}^{\prime }}}{{{\text{T}_{3}}{\text{T}_{4}}{\text{T}_{5}}{\text{T}_{6}}}}=\frac{{{\text{T}_{2}}{\text{T}_{4}}^{\prime }{\text{T}_{5}}^{\prime }}}{{{\text{T}_{4}}{\text{T}_{5}}{\text{T}_{6}}}}

olacaktır. Dikkat edilir ise, payda bulunan bütün dişli sayıları tahrik eden dişlilerdir; paydada bulunan dişli sayıları ise tahrik edilen dişlilere aittir. Ayrıca her bir dış dişli çifti hız oranının işaretini değiştireceğinden çift sayıda dış dişli çifti olduğu durumlarda giriş ve çıkış uzuvları aynı yönde dönerken tek sayıda dış dişli var ise giriş ve çıkış uzuvları birbirlerine göre ters yönde döneceklerdir. İç dişlinin ise yön değiştirmede etkisi yoktur. Birleşik dişli için çıkardığımız bu neticeyi genelleştirirsek:

\displaystyle {\text{R}_{\text{ij}}}={\text{N}_{\text{ij}}}=\frac{{{\text{n}_{\text{1j}}}}}{{{\text{n}_{\text{1i}}}}}={{\left( {-1} \right)}^{\text{k}}}\frac{{\text{Tahrik eden diş sayılarının çarpımı}}}{{\text{Tahrik edilen diş sayılarının çarpımı}}}

Bu denklemde k dış dişli çifti sayısıdır. Önemli bir not ise, diğer mekanizmalarda hız analizi sırasında açısal hız için radyan/saniye kullanılması gerekli iken, burada hızların oranı söz konusu olduğundan açısal hız birimi olarak devir/dakika veya radyan/saniye veya uygun herhangi bir başka birim kullanılabilir ve giriş için kullanılan birim ne ise, o birime göre sonuç elde edilir.

Hız oranı sabittir. Öyle ise, açısal konum hız oranının zamana göre integ-ralinden açısal ivme oranı ise hız oranının zamana göre türevinden bulunabilir. Örneğin eğer i uzvu Δθ_1i kadar döndü ise, j uzvunun dönme miktarı Δθ_1j = R_ijΔθ_1i olacaktır.

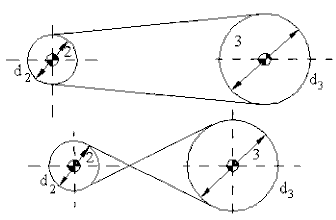
Birleşik basit dişli zincirler için elde etmiş olduğumuz bu genel denklemi diğer lineer mekanik sistemler içinde kullanmamız mümkündür. Şekilde görülen kayış kasnak sisteminde, kaymanın olmadığı var sayılır ise, hız oranları çap oranı olacak, açık kayış sistemi ise, içden dişli çifti gibi olup kayış ile bağlanan her iki uzuvda aynı yönde dönecektir. Merdaneli sistemlerde diş sayısı yerine çap kullanılabilir. Zincir dişli için yine diş sayısı kullanılacaktır. Bu durumda:

\displaystyle {\text{R}_{\text{ij}}}=\frac{{{\text{n}_{\text{1j}}}}}{{{\text{n}_{\text{1i}}}}}={{\left( {-1} \right)}^{\text{k}}}\frac{{\text{Tahrik eden kasnak (merdane, dişli) çapı}}}{{\text{Tahrik edilen kasnak (merdane, dişli) çapı}}}

Bu denklemde k merdanelerde, dıştan temas sayısına, kayışlarda ise, çapraz bağlantı sayısına eşittir.

Açık kayış:          \displaystyle {\text{R}_{{23}}}=-\frac{{{\text{d}_{2}}}}{{{\text{d}_{3}}}}         ,         Çapraz kayış:          \displaystyle {\text{R}_{{23}}}=+\frac{{{\text{d}_{2}}}}{{{\text{d}_{3}}}}

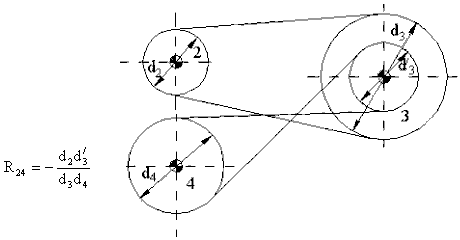
Yukarıda basit bir birleşik kayış-kasnak sistemi ve hız oranı gösterilmektedir.

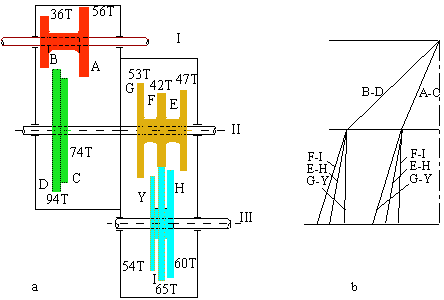
Basit dişli zincirlerinin yoğunlukla kullanıldığı durumlardan biriside, sabit giriş hızına karşı çıkış milinden kademeli değişik hızların elde edilmesidir. Araçların dişli kutusu veya takım tezgahlarında kullanılan dişli kutuları tipik örneklerdir. Kademeli dişli kutuları olarak adlandırabileceğimiz bu tip sistemlerde her hız durumunda farklı bir basit dişli zinciri oluşacaktır. Aşağıdaki şekillerde iki örnek gösterilmektedir. Bu şekillerde ön görünüm kullanıldığı takdirde iç içe değişik çapta daireler görüleceğinden ve hangi uzuvların dişli çifti oluşturduğunu belirlemek zor olduğundan genellikle yan görünüş kullanılır.

Araç dişli kutusu

Bu tür dişli kutularında bir başka özellik ise, giriş ve çıkış millerinin aynı eksende olabilmesi için dişli çifti oluşturan iki uzvun yarı çapları toplamı her kademede eşit olmasıdır. Bu, dişli çifti oluşturan uzuvların diş sayıları toplamının her kademede eşit olmasını gerektirir (diş sayısı farkı bir veya iki diş olduğundada eksenlerin aynı olması sağlanabilir). Örneğin üstteki şekilde A + B = C + F = D + G = E + H = 60 diştir. Alttaki şekilde ise bu toplam 42 dişdir, bu tip dişli kutularına eksenel dişli kutusu diyeceğiz.

Takım tezgahı dişli kutusu

Örnek:

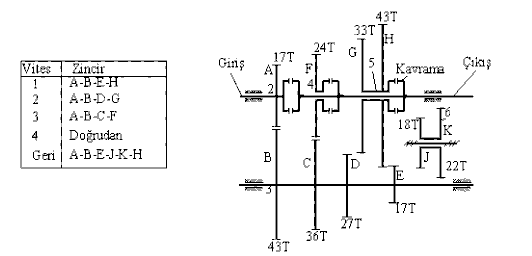
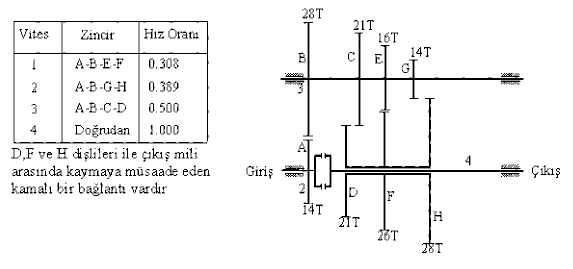
Şekilde 6 vitesli bir takım tezgahı dişli kutusu görülmektedir. 6 vites için hız oranlarını bulmamız gerekmektedir.

Altı kademeli takım tezgahı dişli kutusu

I ve II milleri arasında iki değişik hız oranı elde edilebilecek, II ve III milleri arasında ise üç değişik hız oranı elde edilebilecektir ve bu şekilde I ve III mili arasında 6 değişik hız oranı elde edilecektir. Dikkat edilir ise, iki mil arasında bulunan ve dişli çifti oluşturan dişlilerin diş sayıları toplamı aynıdır. Bu özellik tasarımda önemli sınırlamalar getirir. Zincirler A-C-F-I, A-C-E-H, A-C-G-Y, B-D-F-I, B-D-E-H ve B-D-G-Y dir. Her bir zinciri ayrı ayrı çözmektense I ve II mili arasında bulunan iki hız oranı, II ve III mili arasında bulunan üç hız oranı çözüldükten sonra bunların çarpımı bize hız oranlarını verir. Hız oranlarını bir diagram şeklinde gösterilmesi ise Şekil. (b) de gösterildiği gibi olabilir. I, II ve III milleri çizildikten sonra I ve II arasında bulunan iki hız oranı (56/74 = 0.7568, 36/94 = 0.3830) belirlenerek belirli bir ölçek kullanılarak çizilir. II ve III milleri arasında F-I, E-H veya G-J dişli çiftleri oluşacağından dolayı, üç değişik hız oranı (53/54 = 0.9815, 47/60=0.7833, 42/60 = 0.6462) bulunur. I – II milleri ile II – III milleri arasında hız oranları birbirleri ile çarpılarak I-III mili arasında bulunan 6 değişik hız oranı elde edilmiş olur ve bu oranlar yatay eksende belirli bir ölçek ile gösterildiğinde hız oranlarının boyutları görsel olarak görülecektir. Genel olarak bu tür dişli kutularında hız oranlarının geometrik bir seri takip etmesi istenilir.

ÇEVRENİZDE ERİŞEBİLECEĞİNİZ BİR BASİT DİŞLİ KUTUSUNU İNCELEYİN. BAZILARINDA DİŞLİLERİN ÇOK İLGİNÇ ŞEKİLLERDE MONTE EDİLDİĞİNİ GÖRECEKSİNİZ.