5.1 Mekanizmalarda Ani Dönme Merkezlerinin Bulunması

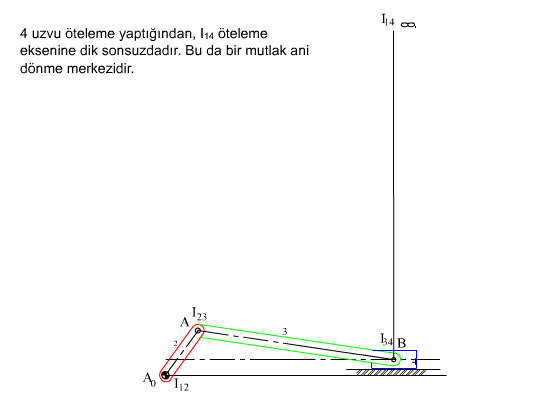
Bir rijit cisim sabit bir eksen etrafında dönüyor ise, ani dönme merkezi bu eksenin merkezi ile çakışır ve bu nokta sürekli olarak aynıdır (sürekli dönme merkezidir). Cisim öteleme yapıyor ise, ani dönme merkezi öteleme eksenine dik yönde sonsuzdadır. Bu şekilde her türlü düzlemsel hareket hız analizi açısından anlık bir dönme olarak incelenebilecektir.

Dikkat edilmesi gereken bir başka nokta ise, bir cismin hareketi bir referans eksenine göre inceleneceğidir. Bu referans ekseni bir sabit cisim üzerinde olabileceği gibi hareketli bir cismin üzerinde de bulunabilir. Bu nedenle eğer düzlemsel hareket sabit bir referans eksenine göre ise, bu durumda mutlak ani dönme merkezi, referans ekseni hareketli bir düzlem üzerinde ise bağıl ani dönme merkezi denecektir. Yukarıda varılmış olan sonuçlar mutlak ani dönme merkezi içindir. Örneğin bağıl ani dönme merkezi durumunda o noktanın hızının sıfır olduğunu söylemek mümkün değildir. Ancak bağıl ani dönme merkezinde çakışan referans ekseninin bulunduğu düzlem üzerindeki nokta ile hareketini incelediğimiz cisim üzerinde bulunan noktaların arasında bağıl hız sıfır olacaktır. Bu nokta göz önüne alınarak ani dönme merkezi şu şekilde tanımlanır: Düzlemsel hareket yapan iki farklı cisim üzerinde bulunan birbirlerine göre bağıl hızları sıfır olan anlık çakışan iki nokta ani dönme merkezidir. Bu durumda l uzuvlu bir mekanizmada o an için her iki uzuv arasında bir ani dönme merkezi olacağına göre (l nesne ikişer ikişer alınıyor), ani dönme merkezi sayısı:

N = l(l − 1)/2

olacaktır. Mekanizmalar için cisimlerimiz uzuvlar olduğundan ve ani dönme merkezi iki uzuv arasında anlık çakışan bir nokta olacağından, ani dönme merkezlerini I_ij olarak gösterelim. Burada i ve j o ani dönme merkezi ile ilgili iki uzvun numarasıdır (I_ij = I_ji olup indis sıralı değildir).

Aranhold-Kennedy Teoremi:

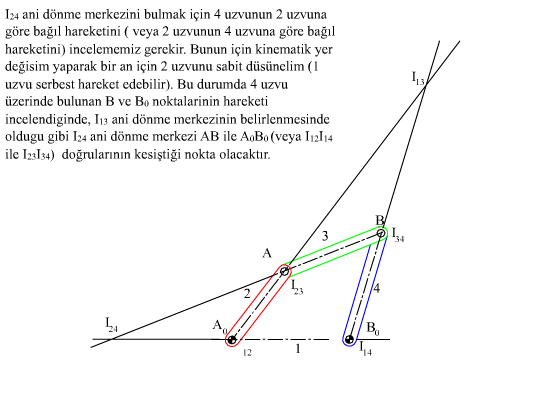
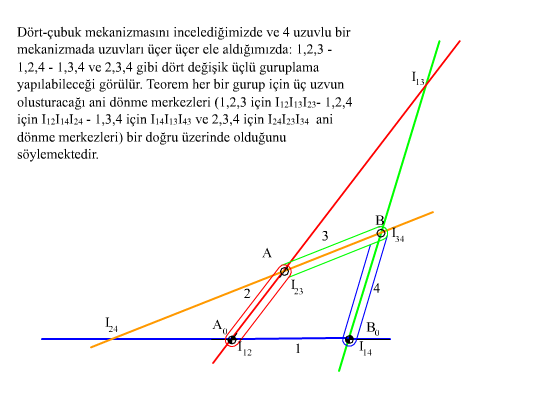
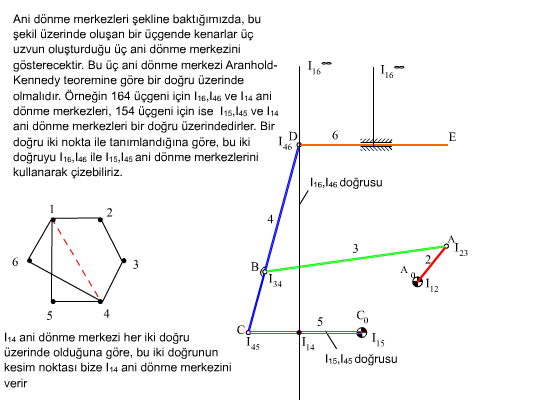
Düzlemsel hareket halinde üç cismin birbirlerine göre ani dönme merkezleri daima bir doğru üzerindedir.

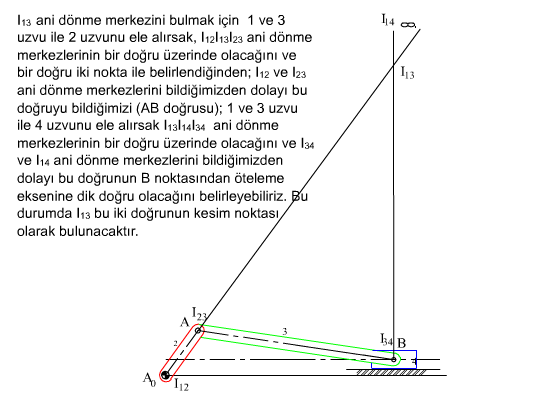
Bir farklı örnek olarak da yukarıda de gösterilen kam mekanizmasını ele aldığımızda, I₁₂ ve I₁₃ ani dönme merkezleri döner mafsal merkezlerindedir. I₂₃ ani dönme merkezi Aranhold-Kennedy teoremine göre I₁₂I₁₃ doğrusunun üzerinde olması gereklidir. Bir başka doğru ise 3 uzvunun 2 uzvuna göre hareketi incelendiğinde bu bağıl hareketin dönme merkezi mutlaka temas noktasında temas eden eğrilerin ortak teğetine dik olması şartından elde edilecektir. Öyle ise I₂₃ ani dönme merkezi I₁₂I₁₃ doğrusu ile temas yüzeyine dik doğrunun kesim noktasıdır.

Bu çözümün AutoCad kütüğü için burayı tıklayınız.

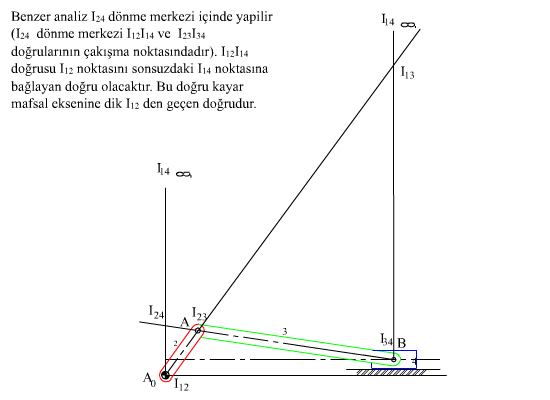
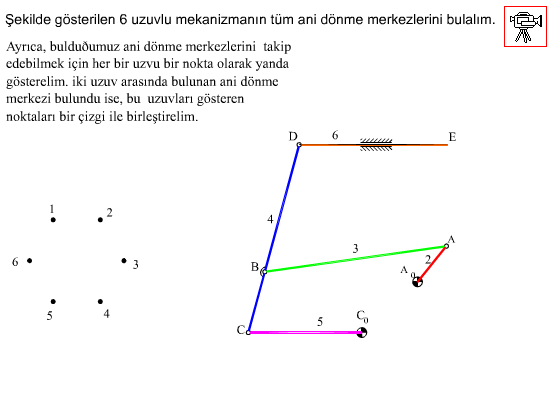
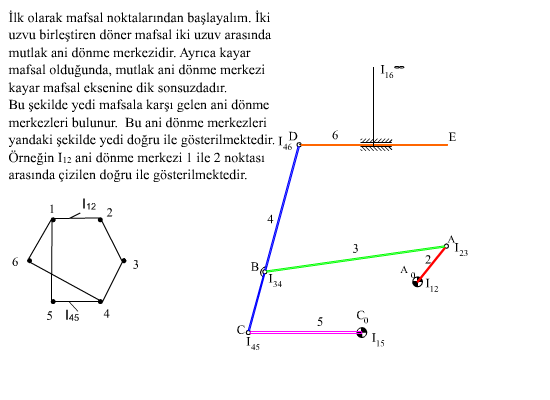
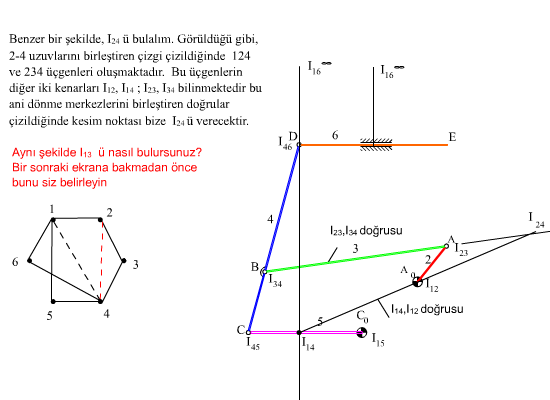
İkinci bir örnek olarak aşağıda 6 uzuvlu bir mekanizma gösterilmiştir. Ani dönme merkezi sayısı N = 6×5/2 = 15 olacaktır. Sistematik bir şekilde probleme yaklaşmak için ilk olarak mafsal eksenleri olan mutlak ani dönme merkezleri olarak belirlenir (kayar mafsallarda bu kayma eksenine dik ve sonsuzda bir noktadır). Bundan sonra her bir uzvu bir nokta ile gösteren bir diyagram çizilir. İki uzuv arasında bulunan ani dönme merkezi belirli ise bu diyagramda iki uzvu gösteren noktalar bir doğru ile bağlanır. Eğer tüm noktalar birbirleri ile bağlanmış ise tüm ani dönme merkezleri belirlenmiş olacaktır. Şekil I-a’da diyagram üzerinde sürekli dönme merkezleri işaretlenmiştir (yedi mafsal ile yedi dönme merkezi belirlidir). Bu diyagram ve mekanizma şeklini kullanarak ve Aranhold-Kennedy teoremi yardımı ile I_ij ani dönme merkezini bulmak için eğer i ve j uzuvları ile birlikte I_piI_pj ile I_qiI_qj ani dönme merkezlerini bildiğimiz p ve q uzuvlarını bilir isek I_piI_pj doğrusu ile I_qiI_qj doğrusunun kesiştiği nokta I_ij ani dönme merkezini belirleyecektir. Diyagramda ise i, j ,p noktaları ile i, j, q noktaları iki farklı üçgen oluşturmakta ve bu üçgende ij kenarı ortak kenar olmaktadır. Öyle ise diyagramda ij doğrusunu çizdiğimizde iki üçgen oluşturabilir isek, bu üçgenlerin diğer kenarları ile belirlenen ani dönme merkezlerini birleştiren doğruların kesişme noktası bize I_ij ani dönme merkezinin yerini belirleyecektir. Şekil I-b’de I₂₄ ani dönme merkezini gösteren 2-4 doğrusunu çizdiğimizde (kesik çizgi) 124 ve 234 üçgenleri oluşmaktadır. Bu üçgenlerin diğer iki kenarları ile belirlenen ani dönme merkezlerini birleştiren doğrular (I₁₂I₁₄ ile I₂₃I₃₄) I₂₄ de kesişirler.

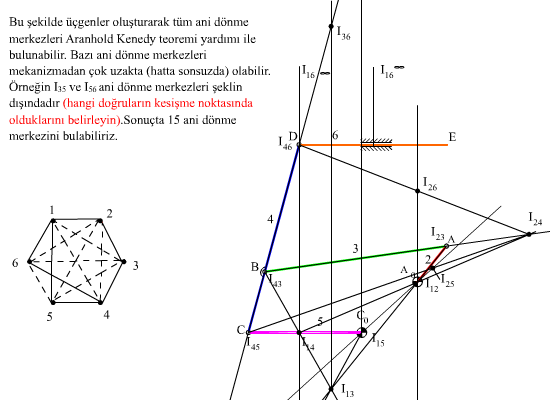
İşlem bu şekilde tekrarlandığında, mafsallar ile belirlenen dönme merkezleri kullanılarak sıra ile diğer tüm ani dönme merkezleri belirlenebilir (Şekil I-c).

Bazı ani dönme merkezlerinin uzak noktalarda olması bilgisayar ortamında çizim yapıldığında bir sorun yaratmayacaktır (Şekil de I₄₆ ve I₃₆ ani dönme merkezleri uzak noktalardadır). Bazı durumlarda bir ani dönme merkezi bilinen ani dönme merkezleri ile hemen belirlenemez. İstenilen ani dönme merkezini belirlemek için başka ani dönme merkezlerini bulmamız gerekebilir. İleride göreceğimiz gibi, tüm ani dönme merkezlerini bulmamıza gerek yoktur. Sadece kullanmamız gereken ani dönme merkezlerini belirlemek yeterlidir.

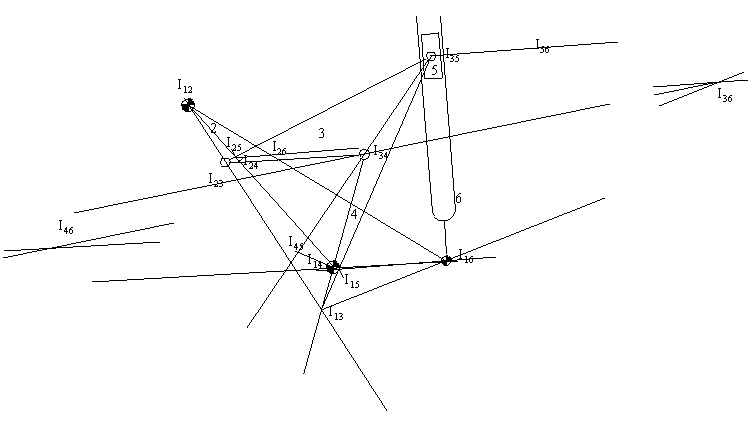
6 Uzuvlu Mekanizma

Bu örneğin çizim kütüğü için tıklayın.

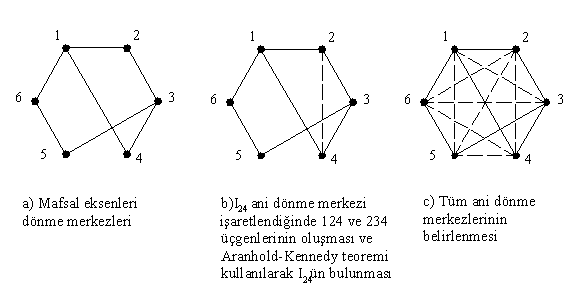
Şekil I Ani dönme merkezleri diyagramı