3.1 Bir Noktanın Kinematiği
Herhangi bir cismin veya noktanın konumu mutlaka bir referans sistemine göre belirlenir. Örneğin bir noktayı üzerinde bulunduğu rijit cisme bağlı bir referans sistemine göre belirlediğimizde sabit boyutlar noktanın konumunu belirler. Buna karşın hareket eden veya duran bir başka uzvun üzerinde bulunan bir referans sistemine göre aynı noktanın konumu, farklı değişken değerlerle belirlenir. Referans sistemine göre konumu belirlemek için farklı parametreler kullanılabilir.
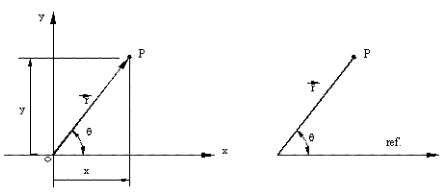
Şekilde de gösterilmiş olan P noktasının konumu O merkezli referans sistemine göre OP uzaklığı ile OP doğrusunun her hangi bir sabit referans doğrusu ile yaptığı açı ile belirlenebilir. Bu iki değer, bilindiği gibi şiddet ve yön içerdiği için bir vektörel büyüklüğü gösterir. Öyle ise bir noktanın konumu OP = r konum vektörü ile belirlidir. Konum vektörünün OP uzunluğu ve yön açısı ile belirlenmesi kutupsal (polar) gösterimdir. İstenildiğinde bir dik koordinat eksen takımı kullanılarak OP vektörü dik yönde iki bileşenin değeri ile de gösterilebilir. Bu durumda:
r = xi + yj
Bu denklemde i ve j, x ve y yönünde birim vektörlerdir (şiddeti bir birim olan vektör). x ve y değerleri OP doğrusunun bu yönlerde iz düşümleridir.
Kutupsal eksen kullanıldığında ise: r = r∠θ
Bu denklemde r, OP uzunluğu, θ ise referans doğrusuna göre OP nin yaptığı açıdır. Açı daima saat yelkovanına ters yönde (SYT) pozitif olacak şekilde ölçülecek, eksi açı değerleri saat yelkovanı (SY) yönünde bir açıyı gösterecektir. Genellikle açının ölçüldüğü referans doğru, pozitif x ekseni yönü alınır. Çünkü bu şekilde kutupsal gösterimden dik eksen takımı gösterimine kolayca geçilebilir. İleride göreceğimiz gibi, mekanizma analizi sırasında bu dönüşüm her an gerekli olabilir.
x, y ve r, θ arasında dönüşümler:
x = r cosθ y = r sinθ r = \displaystyle \sqrt{{{{x}^{2}}+{{y}^{2}}}} θ = tan-1(y/x)
denklemleri kullanılarak sağlanabilir.
Bir noktanın konumunu belirlemek için karmaşık sayılarda kullanılabilir. Karmaşık sayılar vektör olmamalarına rağmen (örneğin vektörler için tanımlanmış olan vektörel çarpım veya skaler çarpım kavramları karmaşık sayılar kullanıldığında bir anlam taşımaz), bir noktanın konumunu belirlemek için rahatlıkla kullanılabilir. Bunun için dik koordinat eksenlerinden x eksenini gerçek, y eksenini ise sanal eksen olarak tanımlamamız gerekir. Bu şekilde elde edilen diyagrama Gauss-Argand diyagramı denir. Bu tanımla P noktasının konumu z karmaşık sayısı ile:
z = x + iy
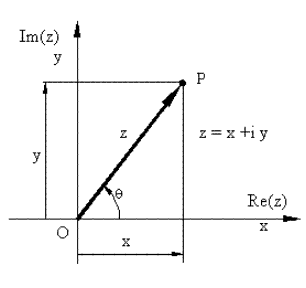
Burada x ve y reel (Re) ve sanal eksenler (Im) yönünde OP nin izdüşümü olup i bir reel sayıyı 90° saat yönüne ters yönde döndüren dönme operatörüdür ( \displaystyle {i=\sqrt{{-1}}} ).
Karmaşık sayılar ile ilgili bilgiler Ek 1 olarak verilmektedir. Karmaşık sayıların mekanizma analizinde en önemli faydası kutupsal gösterimde kullanılan parametreler (r, θ) ile gerekli hesaplamaların yapılabilmesi ve gerektiğinde kolaylıkla dik eksen takımı parametrelerine (x, y) geçilebilmesidir. Bunun için (r, θ) parametreleri ile yazdığımız bir noktanın konumunu gösteren z karmaşık sayısı:
z = r cosθ + i r sinθ = r (cosθ + i sinθ)
Euler denklemi: eiθ = cosθ + i sinθ kullanılarak z kolaylıkla bir üstel fonksiyon haline getirilerek yazılabilir:
z = reiθ = r cosθ + i r sinθ
Üstel fonksiyon şeklinde yazılmış olan bu karmaşık sayıda katsayı (r) uzunluğu (veya vektörün şiddetini) eiθ ise OP yönünde bir birim vektörü göstermektedir (eiθ = cosθ + i sinθ). r kompleks sayının modülü, θ ise kompleks sayının argümanıdır. Bir sayı eiθ ile çarpıldığında Gauss Argand diyagramında θ açısı kadar saat yelkovanına ters yönde dönecektir (Ek 1 e bakınız).
Genellikle bir noktanın konumu zamana göre değişir (zamanın fonksiyonudur). Bu değişim genellikle (r, θ) veya (x, y) parametrelerinden birisinin sabit diğerinin değişken olması ile gerçekleşir. Karmaşık sayılar ile bir noktanın konumu gösterilirken konum vektörleri bu değişik durumlara göre kutupsal veya dik eksen takımı ile aynı denklem içinde gösterilebilir ve elde edilen denklemlerde gerekli tüm matematiksel işlemler tıpkı reel denklemlerde olduğu gibi yapılabilir.
![]() Vektörleri ve karmaşık sayıları üzerlerinde bir ok ile göstermektense, koyu yazarak göstermeyi tercih edeceğiz.
Vektörleri ve karmaşık sayıları üzerlerinde bir ok ile göstermektense, koyu yazarak göstermeyi tercih edeceğiz.