Appendix-1   

Complex Numbers

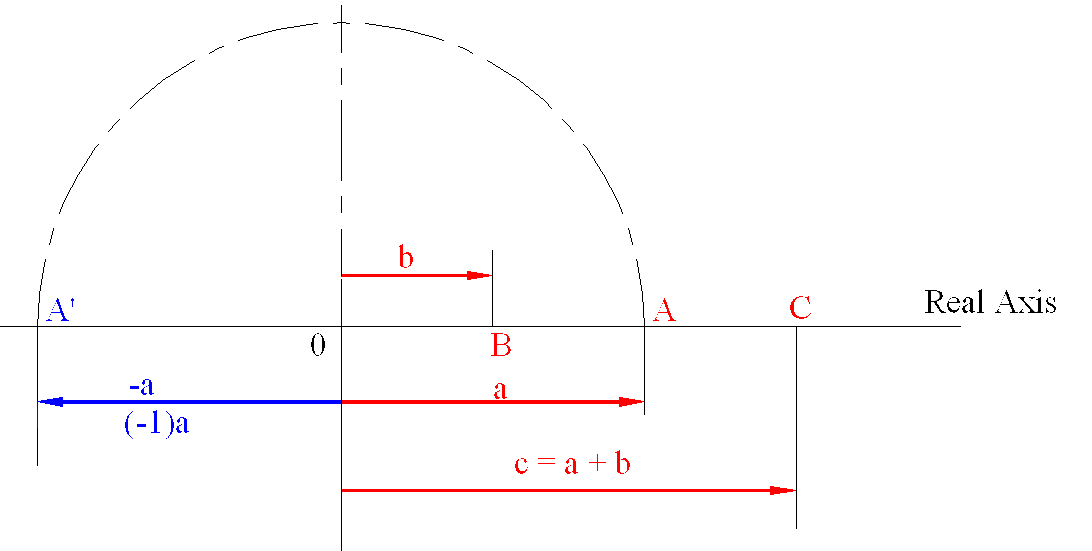
Real numbers are used to show the magnitude of a quantity such as weight, length, etc. In all measuring instruments this number (corresponding to a certain quantity) is shown on a certain scale which is indicated by a dial. Hence a real number can be displayed as points on a straight line with a point 0 as the origin. If we want to add two numbers a and b, we lay off a and starting from the tip of a we lay off b to obtain c= a +b

Usually movement to the right of origin is used to indicate positive numbers. Negative numbers are than shown to the left of the origin and are obtained from the positive numbers by the operator (-1 ). The distance OA and OA’ are equal (a) but they are 180^o apart. Meaning, if we consider a positive real number, a (shown as OA), and rotate it about 0 by 180^o in counterclockwise direction, we end up with OA’, which is -a. In this sense we can think of (-1 ) as an operator which operates on numbers and rotates them, by 180^o CCW. If (-1 ) operates on a twice, we end up with a (OA), since OA has rotated by 360^o ((-1) x (- 1)=1).

Let us now consider a new operator, i, which can act on numbers and rotates them by 90^o in counterclockwise direction. If this operator acts on a number twice, we must rotate the number by 180^o CCW. Hence i.i = i² = -1, since 180^o rotation corresponds to (-1) operation. Then i = \displaystyle \sqrt{{-1}}  which is commonly known as the imaginary number.

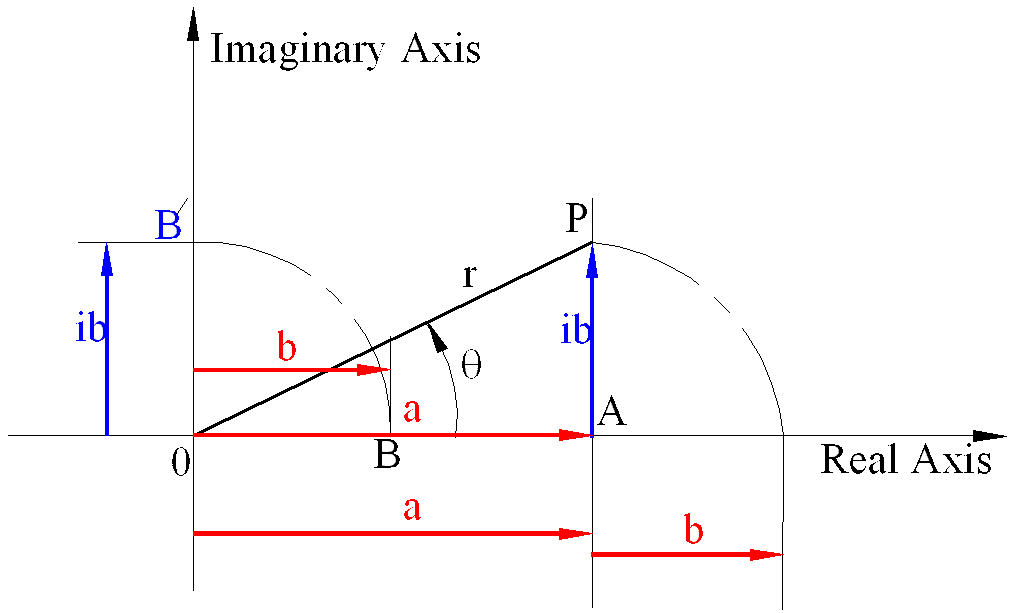
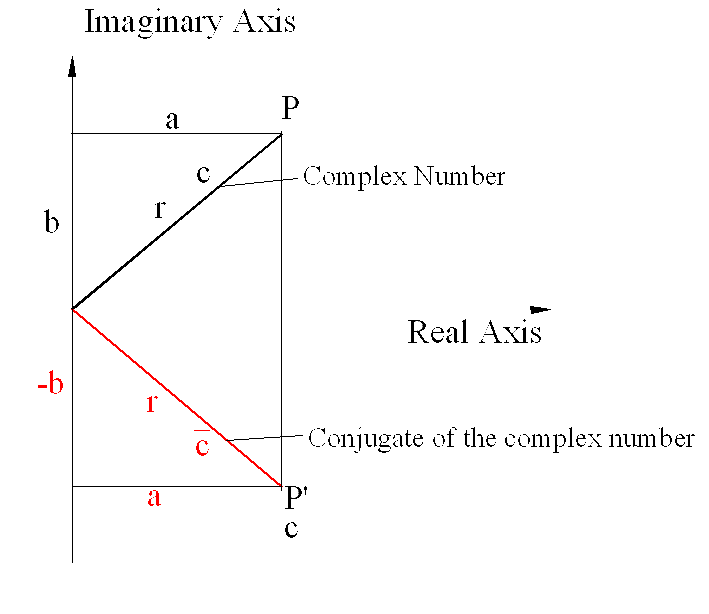
Consider two real numbers a and b. If 90^o CCW turning operation is performed on b, ib will denote a length OB’ rotated 90^o CCW with respect to OB. Now consider c= a + i b. It tells us to consider length a and to it add the length b which is rotated 90^o CCW. Geometrically such a quantity will denote any point, P, on a plane relative to the origin 0. c is known as the complex number. It is an ordered pair of numbers (a, b) which geometrically represents a point on a plane, known as the Gauss-Argand plane, Cauchy plane or complex plane. Hence a complex number can be effectively used instead of a vector representation of position of a point in plane. However, note that a complex number is not a vector.

The absolute value of the complex number is the distance, r, from the origin to the point P (OP) and r =OP= \displaystyle \sqrt{{{{\text{a}}^{2}}+{{\text{b}}^{2}}}} . r = OP is known as the modulus of a complex number. The counter-clockwise angle formed when moving from the real axis to the line OP, (θ), is the argument of the complex number.

We have the following important relations between complex numbers:

a) Two Complex numbers can be equal only if their real and imaginary parts are equal.

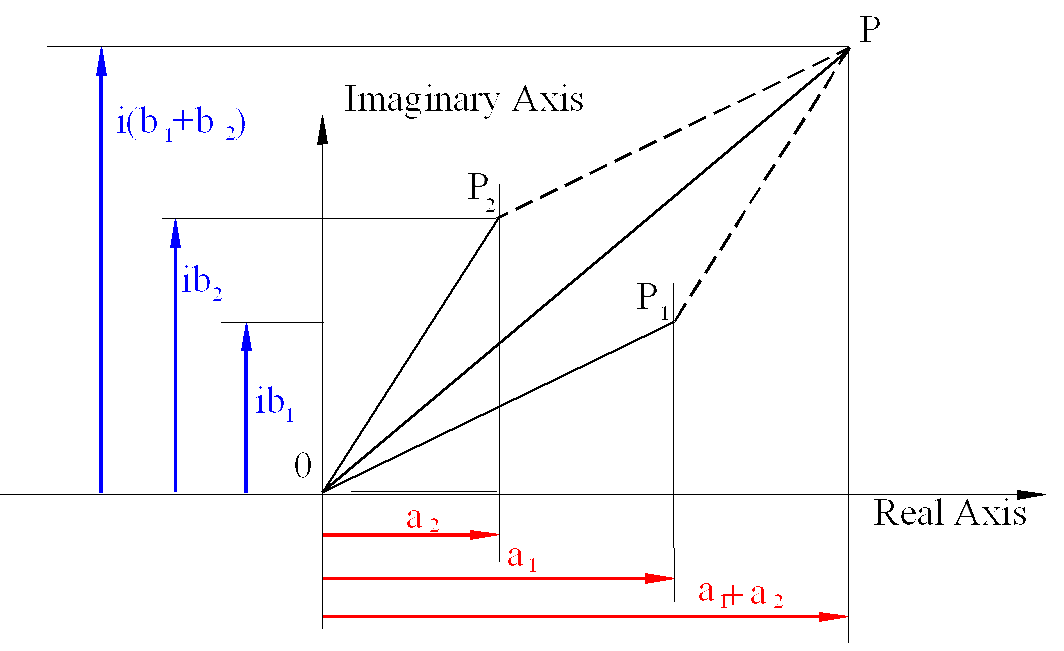
b) Complex numbers add vectorially. The sum of two complex numbers is determined by adding real and imaginary parts separately. If c₁= a₁+ib₁ and c₂= a₂+ib₂ are the two complex numbers, then the sum is given by z as:

z = c₁ + c₂ = (a₁ + a₂) + i(b₁ + b₂)

c) Multiplication and division follows the rules of ordinary algebra with the additional relation i²=-1 .

The complex number representation:

c=a+ib

is known as the orthogonal form. Referring to the figure we have:

a = r cosθ, b = r sinθ

then

c = r(cosθ + i sinθ)

or using Euler’s equation:  e^iθ= cosθ +i sinθ complex number c can be written as:

c = re^iθ

Which is known as the exponential form or polar form of a complex number

If the modulus of a complex number is unity( r =1 ):

u = e^iθ

is a unit vector that makes an angle θ in counterclockwise direction with respect to the positive x axis

When we multiply a complex number c = OP = r e^iθby a real number, k:

c′ = OP′ = kc = kre^iθ

note that the argument of the complex number is unaltered whereas the modulus is now kr. Hence the vector OP has “stretched” to OP’ when multiplied by a real number . Multiplication of a complex number by a constant is known as stretch operation in which the magnitude of the position vector is increased or decreased while the orientation is constant.

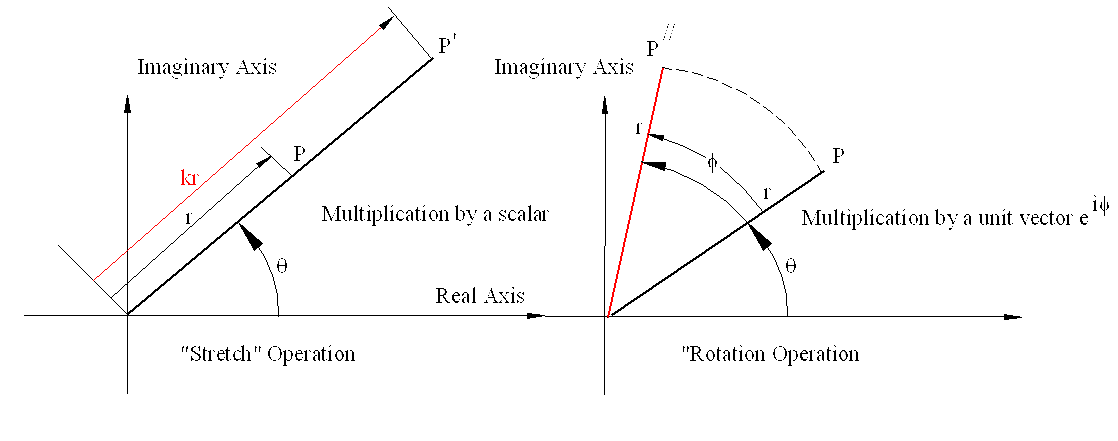
When we multiply a complex number c =reⁱ by a complex number of unit magnitude u = e^iϕ :

c″ = OP″ = u·c = e^iϕ·re^iθ

Using the rules of algebra, if the two powers have the same base, the powers add:

c″ = re^{i(θ + ϕ)}

Now, the magnitude of the vector c is unaltered but the argument is changed from θ to +θ + ϕ. In other words. the vector OP is “rotated” counterclockwise by an angle ϕ açısı (refer to the figure). Hence multiplication by e^iϕ acts as a rotation operator. (Note thate^iπ/2 = i  ve e^iπ = e^{i(π/2 + π/2)} = e^iπ/2·e^iπ/2 = i·i = −1 which rotate a vector by 90^o and 180^o CCW respectively. In other words, e^iϕ confirms the 90^o counterclockwise rotation operator than we have defined previously.

Conjugate of a complex number has the real and imaginary parts equal to the original complex number but the imaginary part is in opposite sign ( see figure.). For example, if c=a+ib is a complex number its complex conjugate, \displaystyle \mathbf{\bar{c}}  (c-bar), is: \displaystyle \mathbf{\bar{c}} =a-ib. or in exponential form: If c=re^iθ, its complex conjugate is \displaystyle \mathbf{\bar{c}} = re^−iθ.

Using the conjugate of a complex number, we have:

r² = c \displaystyle \mathbf{\bar{c}} = (a + ib)(a − ib) = a² + b²

Real part of a complex number is:

Re(c) = (c + \displaystyle \mathbf{\bar{c}} )/2 = (a + ib + a − ib)/2 = a

Imaginary part of a complex number is:

Im(c) = (c − \displaystyle \mathbf{\bar{c}} )/(2i) = (a + ib − a + ib)/(2i) = b

If c₁= a₁+ib₁ and c₂= a₂+ib₂ , the division of these two complex numbers is:

\displaystyle \frac{{{{\mathbf{c}}_{1}}}}{{{{\mathbf{c}}_{2}}}}=\frac{{{{\text{a}}_{1}}+\text{i}{{\text{b}}_{1}}}}{{{{\text{a}}_{2}}+\text{i}{{\text{b}}_{2}}}}

In order to simplify this expression we multiply both the numerator and the denominator by the complex conjugate of the denominator:

\displaystyle \frac{{{{\mathbf{c}}_{1}}}}{{{{\mathbf{c}}_{2}}}}=\frac{{{{\text{a}}_{1}}+\text{i}{{\text{b}}_{1}}}}{{{{\text{a}}_{2}}+\text{i}{{\text{b}}_{2}}}}\cdot \frac{{{{\text{a}}_{2}}-\text{i}{{\text{b}}_{2}}}}{{{{\text{a}}_{2}}-\text{i}{{\text{b}}_{2}}}}=\frac{{{{\text{a}}_{1}}{{\text{a}}_{2}}+{{\text{b}}_{1}}{{\text{b}}_{2}}}}{{{{\text{a}}_{2}}^{2}+{{\text{b}}_{2}}^{2}}}+\text{i}\frac{{{{\text{b}}_{2}}{\text{b}_{1}}-{{\text{a}}_{1}}{{\text{b}}_{2}}}}{{{{\text{a}}_{2}}^{2}+{{\text{a}}_{2}}^{2}}}

\displaystyle \frac{{{{\mathbf{c}}_{1}}}}{{{{\mathbf{c}}_{2}}}}=\frac{{{{\text{r}}_{1}}{{\text{a}}^{{\text{i}{{\text{θ}}_{1}}}}}}}{{{\text{r}_{2}}{{\text{e}}^{{\text{i}{{\text{θ}}_{2}}}}}}}=\frac{{{{\text{r}}_{1}}}}{{{{\text{r}}_{2}}}}{{\text{e}}^{{\text{i}{{\text{θ}}_{1}}}}}{{\text{e}}^{{-\text{i}{{\text{θ}}_{2}}}}}=\frac{{{{\text{r}}_{1}}}}{{{{\text{r}}_{2}}}}{{\text{e}}^{{\text{i}\left( {{{\text{θ}}_{1}}-{{\text{θ}}_{2}}} \right)}}}