Cam Profile for a Radial Cam with Flat Faced Oscillating Follower

In case of a flat faced follower the generating curve which is the follower profile is a straight line. Initially this line is tangent to the base circle radius. For an oscillating flat faced follower, the follower rotates about A₀, which is at a distance a from the cam axis of rotation. The flat face is offset by a distance c (|AC| = c and AC is perpendicular to the follower face). If the cam is to rotated counter clockwise by an angle θ, in the inverted motion the fixed link (A₀O), will rotate clockwise by an angle q and at the same time the follower will rotate relative to the fixed link by an angle ϕ(θ) determined by the motion curve. At an instant the flat face will be at an angle ϕ₀ + ϕ − θ − p/2 with respect to the x axis (selected along A₀O) as shown. The coordinates of point A′ on the follower is:

OA′ = z_a = x_a + iy_a = −ae^−iθ + ce^{i(ϕ₀ + ϕ − θ)}

or

xa = −a cosθ + c cos(ϕ0 + ϕ − θ) ya = a sinθ + c sin(ϕ0 + ϕ − θ)

(1)

Note that x_a and y_a are functions of θ (ϕ is a function of θ only). Hence we can write the equation of the straight line (Generating curve) as:

slope = \displaystyle \frac{{\text{y}}-{\text{y}}_{\text{a}}}{{\text{x}}-{\text{x}}_{\text{a}}}=\tan \left( {\text{ϕ}}_{\text{0}}+{\text{ϕ}}-{\text{θ}}-{\text{π/2}} \right)=\frac{-\cos\left( {\text{ϕ}}_{\text{0}}+{\text{ϕ}}-{\text{θ}} \right)}{\sin\left( {\text{ϕ}}_{\text{0}}+{\text{ϕ}}-{\text{θ}} \right)} 

or

\displaystyle {\text{f}}\left({\text{x, y, θ}}\right)= \left( {\text{x}}-{\text{x}}_{\text{a}} \right)\cos\left( {\text{ϕ}}_{\text{0}}+{\text{ϕ}}-{\text{θ}} \right)+\left( {\text{y}}-{\text{y}}_{\text{a}} \right)\sin\left( {\text{ϕ}}_{\text{0}}+{\text{ϕ}}-{\text{θ}} \right)=0

Taking the partial derivative of the function with respect to q:

\displaystyle {\text{f}}_{\text{θ}}\left({\text{x, y, θ}}\right)=\left[ -\frac{\partial {\text{x}}_{\text{a}}}{\partial {\text{θ}}}+\left( {\text{y}}-{\text{y}}_{\text{a}} \right)\left( \frac{\partial {\text{ϕ}}}{\partial {\text{θ}}}-1 \right)\right]\cos\left( {\text{ϕ}}_{\text{0}}+{\text{ϕ}}-{\text{θ}} \right)-\left[ \frac{\partial {\text{y}}_{\text{a}}}{\partial {\text{θ}}}+\left( {\text{x}}-{\text{x}}_{\text{a}} \right)\left( \frac{\partial {\text{ϕ}}}{\partial {\text{θ}}}-1 \right)\right]\sin\left( {\text{ϕ}}_{\text{0}}+{\text{ϕ}}-{\text{θ}} \right)=0

or

\displaystyle -\left( {\text{x}}-{\text{x}}_{\text{a}} \right)\left( \frac{\partial {\text{ϕ}}}{\partial {\text{θ}}}-1 \right)\sin\left( {\text{ϕ}}_{\text{0}}+{\text{ϕ}}-{\text{θ}} \right)+\left( {\text{y}}-{\text{y}}_{\text{a}} \right)\left( \frac{\partial {\text{ϕ}}}{\partial {\text{θ}}}-1 \right)\cos\left( {\text{ϕ}}_{\text{0}}+{\text{ϕ}}-{\text{θ}} \right)=\frac{\partial {\text{x}}_{\text{a}}}{\partial {\text{θ}}}\cos\left( {\text{ϕ}}_{\text{0}}+{\text{ϕ}}-{\text{θ}} \right)+\frac{\partial {\text{y}}_{\text{a}}}{\partial {\text{θ}}}\sin\left( {\text{ϕ}}_{\text{0}}+{\text{ϕ}}-{\text{θ}} \right)

where:

\displaystyle \frac{\partial {\text{x}}_{\text{a}}}{\partial {\text{θ}}}={\text{a}}\sin{\text{θ}}-{\text{c}}\sin\left( {\text{ϕ}}_{\text{0}}+{\text{ϕ}}-{\text{θ}}\right)\left( \frac{\partial {\text{ϕ}}}{\partial {\text{θ}}}-1 \right) \displaystyle \frac{\partial {\text{y}}_{\text{a}}}{\partial {\text{θ}}}={\text{a}}\cos{\text{θ}}+{\text{c}}\cos\left( {\text{ϕ}}_{\text{0}}+{\text{ϕ}}-{\text{θ}}\right)\left( \frac{\partial {\text{ϕ}}}{\partial {\text{θ}}}-1 \right)

(2)

x − x_a and y − y_a can be linearly soled from f(x, y, q) = 0 and f_q(x, y, q) = 0. We obtain the cam profile as the envelope in parametric form as:

\displaystyle {\text{x}}={\text{x}}_{\text{a}}-\frac{\sin\left( {\text{ϕ}}_{\text{0}}+{\text{ϕ}}-{\text{θ}}\right)}{\partial {\text{ϕ/}}\partial {\text{θ}}-1}\left[ \frac{\partial {\text{x}}_{\text{a}}}{\partial {\text{θ}}}\cos\left( {\text{ϕ}}_{\text{0}}+{\text{ϕ}}-{\text{θ}}\right)+\frac{\partial {\text{y}}_{\text{a}}}{\partial {\text{θ}}}\sin\left( {\text{ϕ}}_{\text{0}}+{\text{ϕ}}-{\text{θ}}\right)\right] \displaystyle {\text{y}}={\text{y}}_{\text{a}}-\frac{\cos\left( {\text{ϕ}}_{\text{0}}+{\text{ϕ}}-{\text{θ}}\right)}{\partial {\text{ϕ/}}\partial {\text{θ}}-1}\left[ \frac{\partial {\text{x}}_{\text{a}}}{\partial {\text{θ}}}\cos\left( {\text{ϕ}}_{\text{0}}+{\text{ϕ}}-{\text{θ}}\right)+\frac{\partial {\text{y}}_{\text{a}}}{\partial {\text{θ}}}\sin\left( {\text{ϕ}}_{\text{0}}+{\text{ϕ}}-{\text{θ}}\right)\right]

(3)

Note that unlike the roller follower, in case of flat faced followers the envelope has one branch. If the cam profile is to be cut with a cutter of radius r_c, the cutter must be tangent to the cam profile. Since at the point of contact P(x, y), the follower face is also tangent, we determine the centre of the cutter as (see the figure below):

xc = x + rc cos(ϕ0 + ϕ − θ) yc = y + rc sin(ϕ0 + ϕ − θ)

(4)

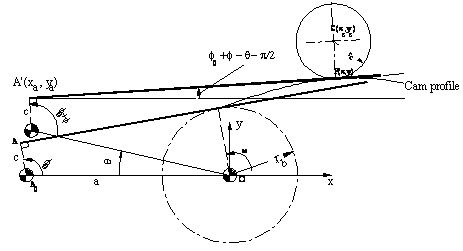
Example 8.8.

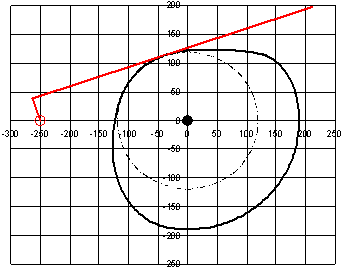
Design a a radial cam with a translating flat faced follower. The follower must rotate 20º CCW for 120º rotation of the cam, dwell at this position for 100º and return to the original position in 90º and dwell at this position for the remaining of the cycle. Assume both the rise and return motions are in cycloidal motion. Let a = 250 mm, r_b = 120 mm and c = 40 mm.

This example has been solved both in Excel and MathCad. First the motion curve and its derivative with respect to the crank angle are determined for every cam rotation angle next for every position x_a, y_a (equation 1) and their derivative with respect to q (dx_a/dq, dy_a/dq, equation 2), are found. Next using equation 3 the coordinated of the cam profile is determined. The result is shown below. If the cam is to be cut with a cutter of 60 mm diameter, the path of the cutter is determined using equation 4.