7.5 FOUR-BAR AND SLIDER-CRANK COGNATES ROBERTS – CHEBYCHEV THEOREM

When our concern is only the path traced by the coupler point of a four-bar or a slider-crank mechanism, we can determine other four-bar or slider-crank mechanism proportions that generate identically the same coupler point curve. The four-bar mechanisms that generate the identical coupler point curve are known as the cognates of a four-bar. Let us state a theorem and show how the cognates of a four-bar and slider crank mechanism can be found.

Roberts-Chebychev Theorem

There are three different four-bar mechanism proportions that will trace identically the same coupler curve.

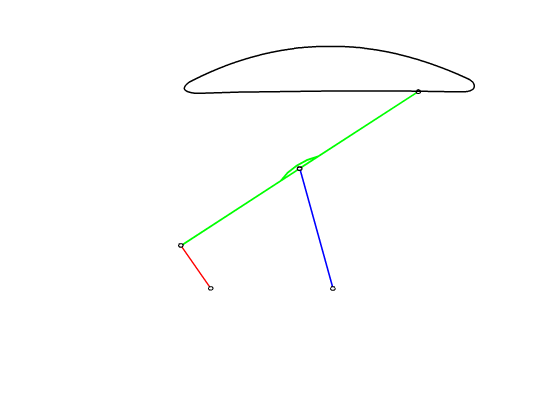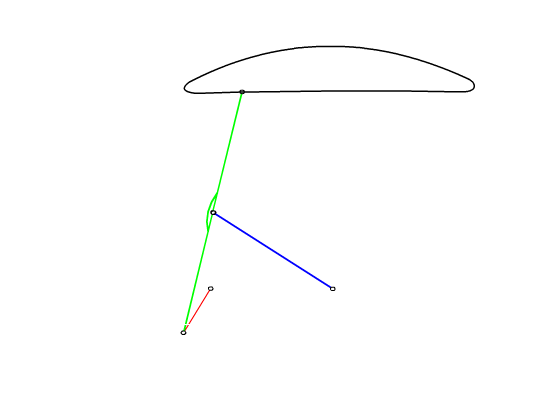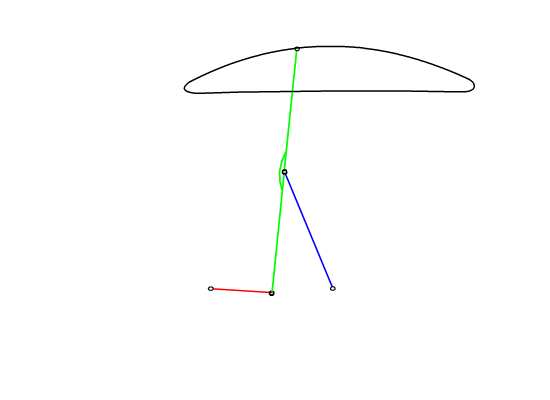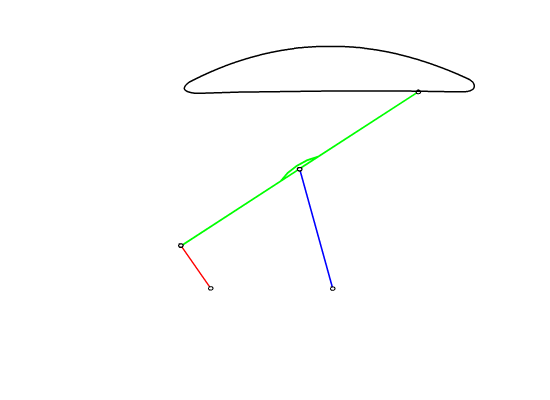
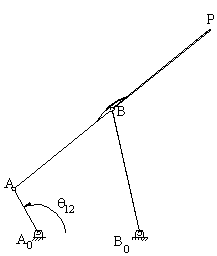
Consider the four-bar mechanism shown (A₀B₀=a₁, A₀A=a₂, AB=a₃, B₀B=a₄, AP=b₃, BP=c₃). The coupler point P traces a curve as shown. For this mechanism the loop equation is:

a₂e^iθ₁₂ + a₃e^iθ₁₃ = a₁ + a₄e^iθ₁₄

(1)

The location of coupler point, P, for any crank angle q₁₂ can be determined from the equations:

Z_P = a₂e^iθ₁₂ + b₃e^{i(θ₁₃+α)}

(2)

Z_P = a₁ + a₄e^iθ₁₄ + c₃e^{i(θ₁₃+π−β)}

(3)

Noting that the angles q₁₃, q₁₄, are determined for every crank angle q₁₂ from the loop equation.

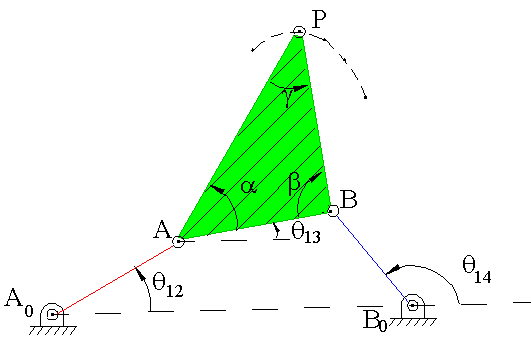
Figure 7.33.

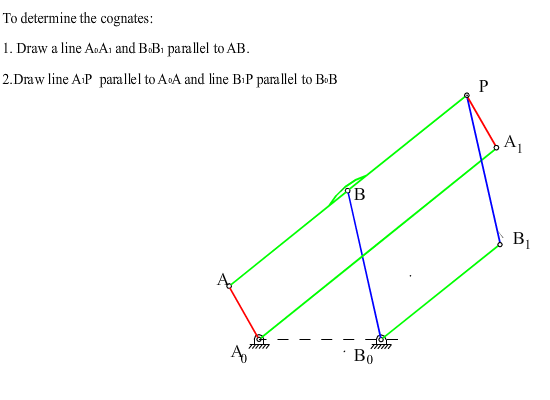
The construction for determining the cognates can be given by the following steps (Fig.7.34):

1. Draw A₀A₁//AP and B₀B₁//BP

2. Draw PA₁//A₀A and PB₁//B₀B

Hence A₀A₁PA and B₀B₁PB form parallelograms. Therefore:

A₀A₁=b₃, A₁P=a₂, B₀B₁=c₃, B₁P=a₄

Also:

< xA₀A₁=q₁₂+a, < xA₁P=q₁₂, < xB₀B₁=q₁₃–b, < xB₁P=q₁₄

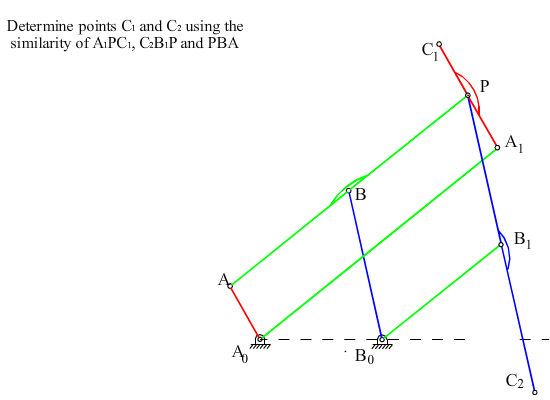
Construct triangles DPA₁B₁ and DPB₁C₂ similar to the triangle DPAB
( < C₂B₁P=< PBA; < PA₁C₁ =< BAP);

From the similarity of the triangles:

or or and similarly

, Also < xA₁C₁=q₁₂+a, < xB₁C₂= q₁₃+p – b,

< xC₂P=q₁₂+a , < xPC₁=q₁₃+p – b.

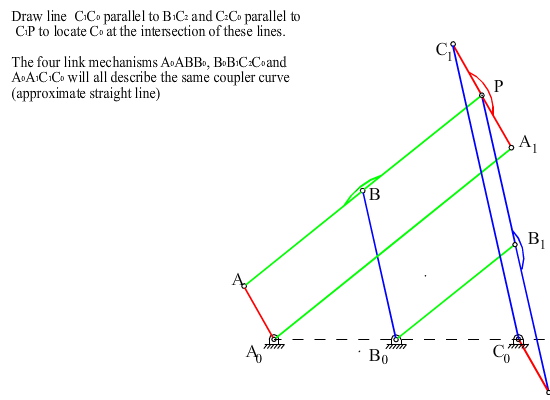
4. Draw C₁C₀ //PC₂ and C₂C₀// C₁P to locate C₀. C₀C₁PC₂ forms a parallelogram therefore:

and < xC₁C₁=q₁₂+a, < xC₀C₂= q₁₃+p – b

5. Four bar mechanisms that trace the same coupler curve are:

A₀ABB₀ (P on AB) (a)

C₀C₁A₁A₀ (P on C₁A₁) (b)

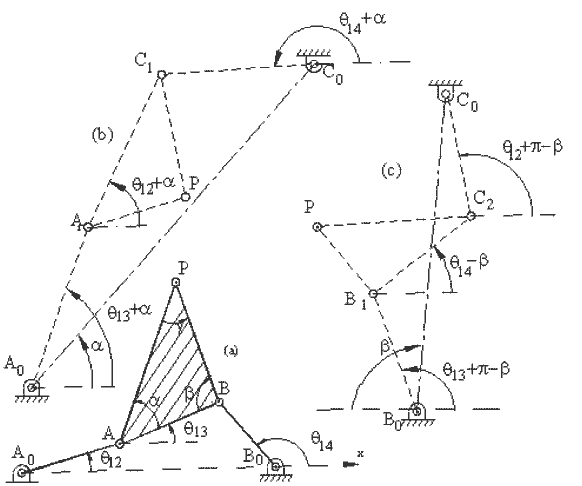
C₀C₂B₁B₀ (P on C₂B₁ ) ( c)

Now, the location of C ₀ can be written as :

A₀C₀ = A₀A₁ + A₁C₁ + C₁C₀

A₀C₀ = A₀B₀ + B₀B₁ + B₁C₂ + C₂C₀

Writing these equations in complex numbers:

A₀C₀ = b₃e^{i(θ₁₃+α)} + (a₂b₃/a₃)e^{i(θ₁₂+α)} − (a₄b₃/a₃)e^{i(θ₁₄+α)}

(4)

A₀C₀ = a₁ + c₃e^{i(θ₁₃+π−β)} + (a₂c₃/a₃)e^{i(θ₁₂+π−β)} + (a₄c₃/a₃)e^{i(θ₁₄−β)}

(5)

Equations (4) and (5) can also be written as:

A₀C₀ = b₃/a₃e^iα(a₂e^iθ₁₂ + a₃e^iθ₁₃ − a₄e^iθ₁₄)

(6)

A₀C₀ = a₁ + c₃/a₃e^i(π−β)(a₂e^iθ₁₂ + a₃e^iθ₁₃ − a₄e^iθ₁₄)

(7)

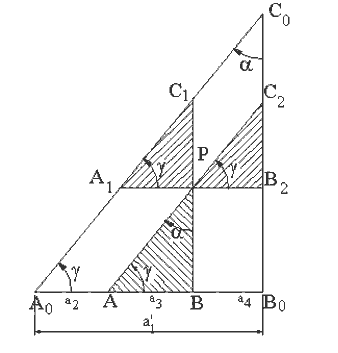
Figure 7.36

From equation (1) the terms inside the parenthesis are equal to a₁. Therefore, all the three four-bar mechanisms satisfy the same loop equation and point C₀ is a fixed point located at a₁b₃/a₃e^iα.The angles q₁₃, q₁₄ and q₁₂

are all related by equation (1) for all the three four-bar mechanisms and the coordinates of the coupler point P on the coupler point of all these three four-bar mechanisms are given by equation (2) or (3). Hence the theorem is proved.

The given procedure locates both the orientation and the lengths of the links for all the four-bar cognates. A simpler construction for determining the link lengths is to stretch the four-bar mechanisms such that A0ABB0 lie on a straight line, since the theorem is also valid for an immovable four-bar with a new fixed link length a’₁=a₂+a₃+a₄. Application of the above steps to such a configuration for determining its cognates is quite simple as shown in the figure. One can then determine the location C₀ of the original configuration by noting

A₀C₀ = a₁b₃/a₃e^iα = a₁ + a₁c₃/a₃e^i(π−β) , |A₀C₀| = a₁b₃/a₃ , |B₀C₀| = a₁c₃/a₃

One can join any two or all three of the cognates by a revolute joint at P and the mechanism thus obtained will still be movable (provided that the cognates are movable). The mechanism will be of permanent critical form (the general degree-of-freedom equation will not apply).

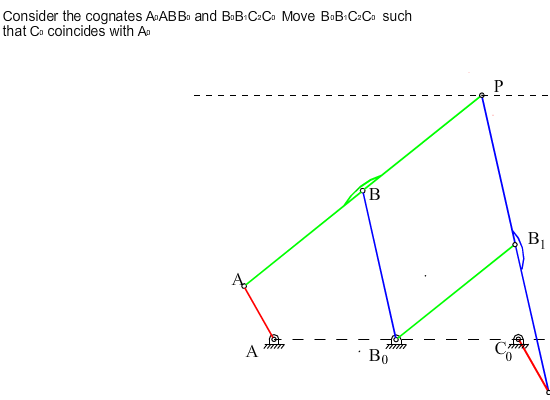
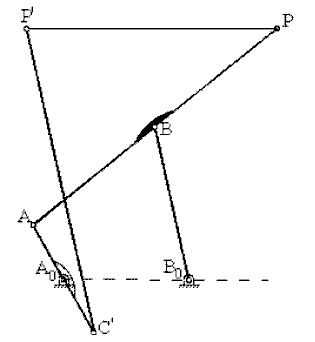
Another important use of the cognates of four-bar mechanisms is to obtain a rigid body motion which is in a translation (e.g. lines taken on this body remain parallel to their original positions) and every point on this body describe paths which are the same as the path of coupler point of the original four-bar.

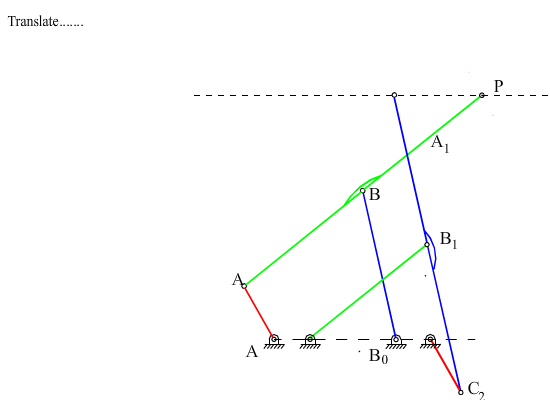
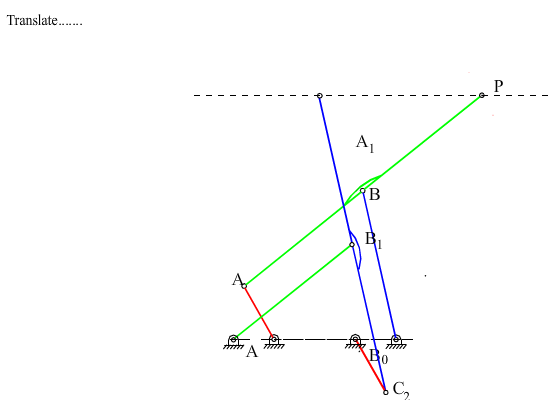
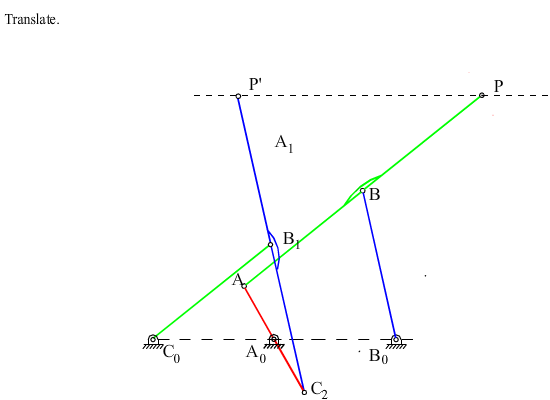
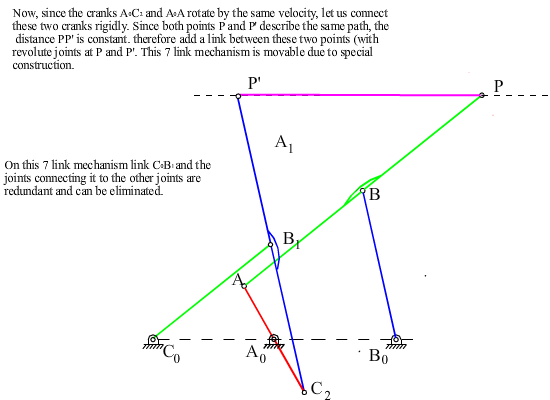
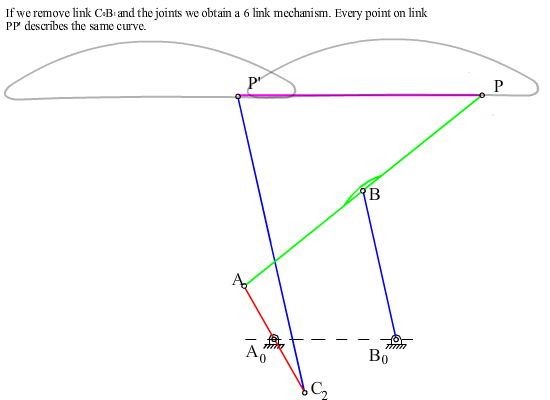
Referring to figures, note that the cranks A₀A and C₀C₂ or B₀B and C₀C₁ or B₀B₁ and A₀A₁ rotate by the same amount although these angles differ by a constant (a or p-b). Let us move one of the cognates relative to the other such that the centers of rotation of the two cranks rotating at the same speed are coincident. For example, if C₀ and A₀ are to be made coincident every point of the cognate C₀C₂B₁B₀ must be displaced parallel to A₀C₀ by an amount |A₀C₀| . The relative positions of all the links of the cognate with respect to each other are kept, e.g. since the cranks C₀C₂ and A₀A rotate at the same speed, their relative positions will not change and hence they can be connected to each other. Now consider points P and P’. Both of these points will always describe the same path and the distance PP’ will not change and will always be parallel to the initial line drawn. Therefore, we can attach a link in between the two points PP’ and connect them by revolute joints to the coupler links of the two four-bars. The seven link mechanism thus obtained is an overclosed mechanism with link PP’ in a translation. We can eliminate this overclosure by removing one of the cranks B₀B or C₀C₂ and obtain a six-link mechanism as shown. The mechanism can still perform a constrained motion with PP’ in translation. Note that the six link mechanism for the required motion is not unique (there are other six-link mechanisms to generate a translation of a link as that of point P.

Example 4.9.

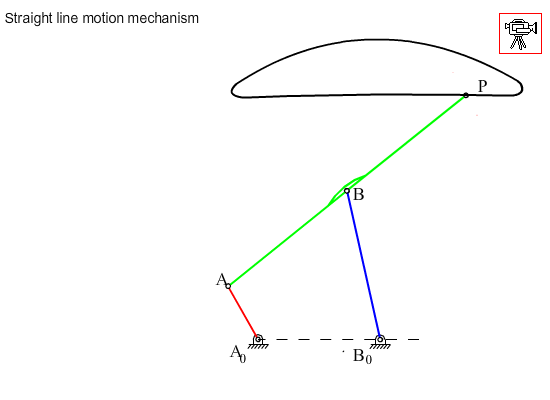
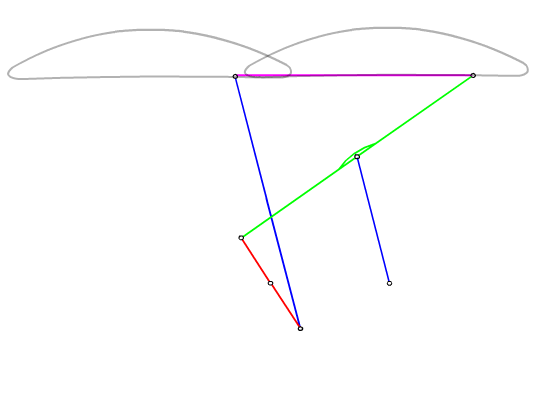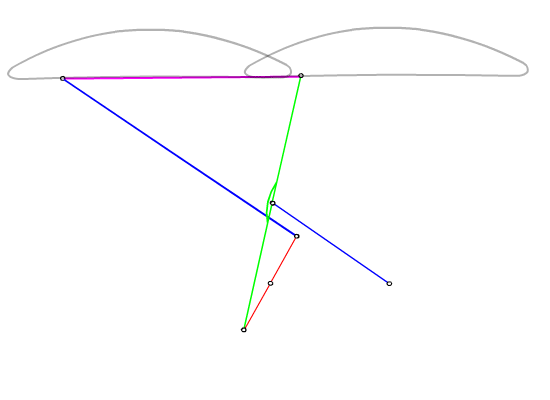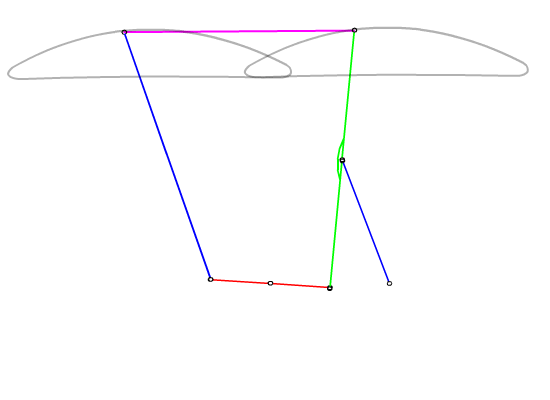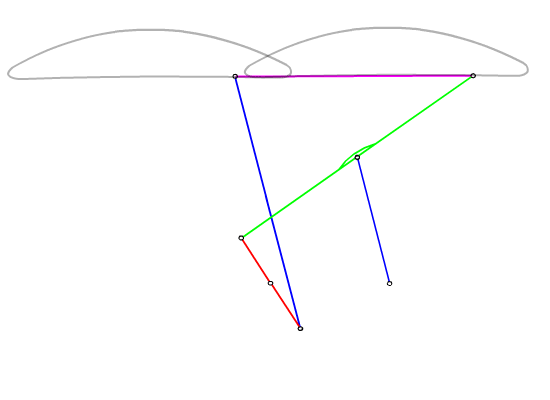
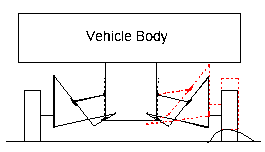
Mechanism shown below is known as Chebyshev lambda or Hoecken straight line mechanism. The coupler point P describes an approximate straight-line. The link length proportions are given as: AB = BP = B₀B = 2.5 A₀A, A₀B₀ = 2 A₀A. We would like to obtain a rigid body in an approximate rectilinear translation guided by a six-link mechanism.

The construction of the cognates and the design of the six link mechanism is shown in the following flash file

Resulting mechanism

This mechanism has been used as the suspension system for an off-road vehicle.

In case of slider-crank mechanisms, there are two different slider-crank proportions that trace the same coupler-point curve. The construction for determining the cognate of a slider-crank mechanism can be outlined by the following steps (Proof is left as an exercise).

1. Draw PA₁//AA₀and A₀A₁//PA
2. Draw triangle DPA₁C₁ similar to the triangle DPAB (< A₁PC₁ = < ABP )

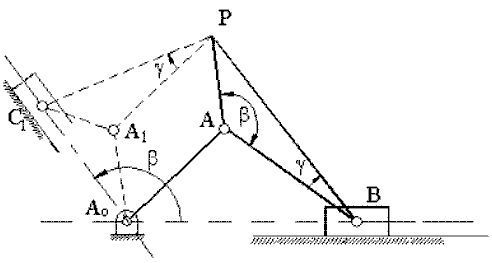
One can also extend A₀AB on a straight line and obtain the link length dimensions as shown..

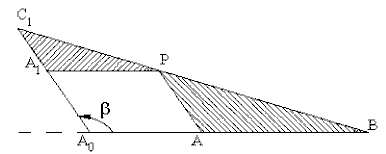
If the designer’s main concern is simply the coupler-point curve, then he can easily replace a four-bar or slider-crank mechanism with its cognates. The cognate may have a better dimensional characteristics.