7.2 Slider Crank Mechanisms

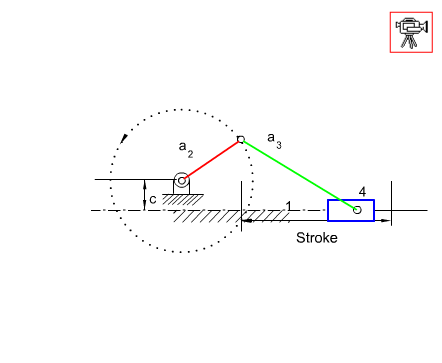
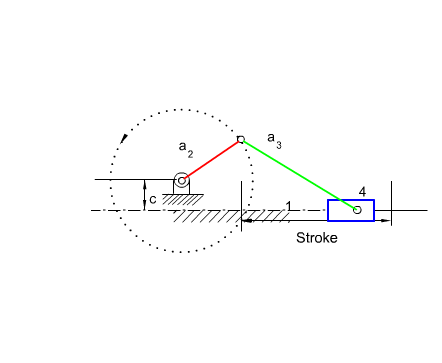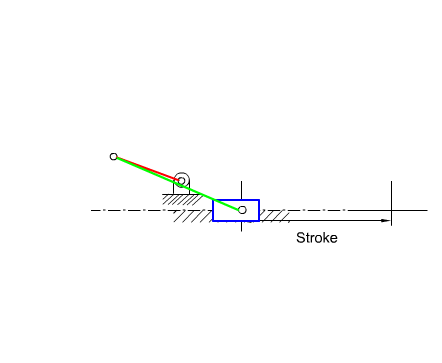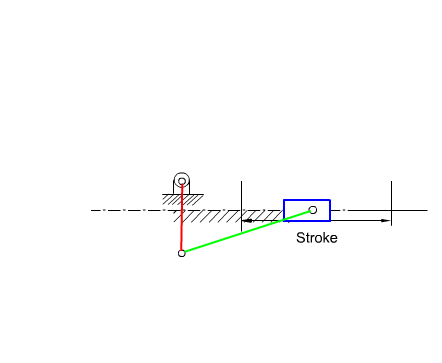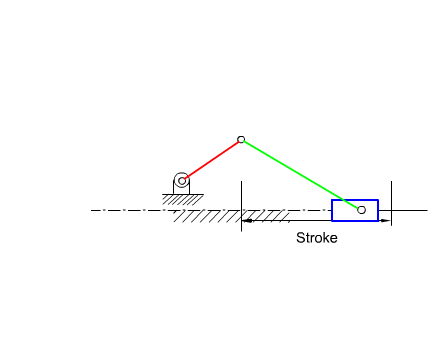
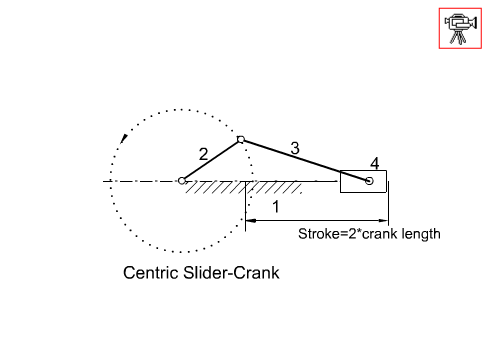
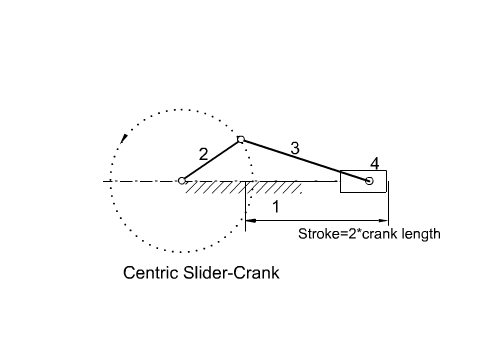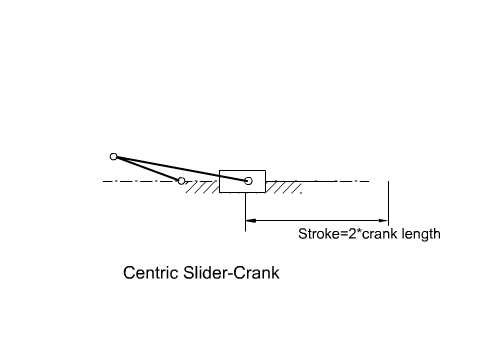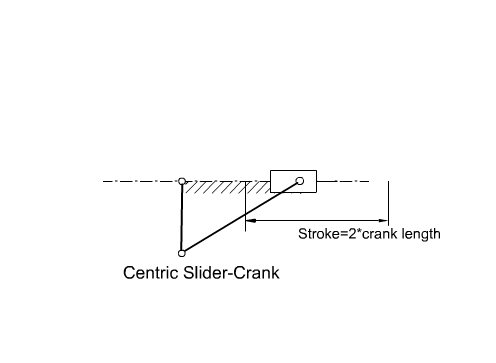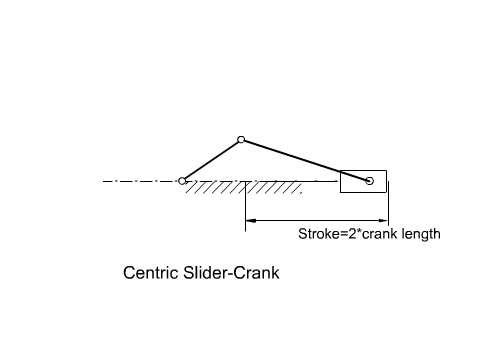
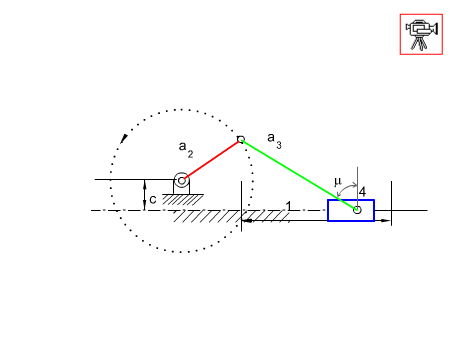
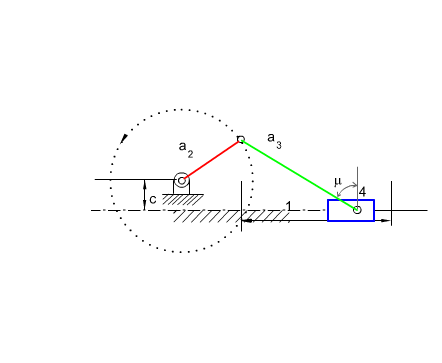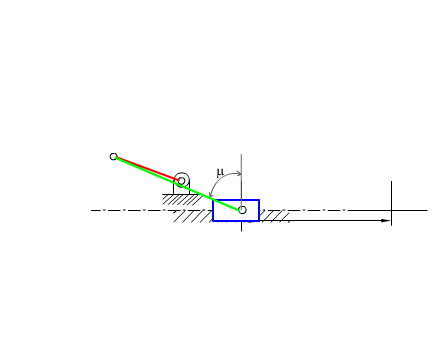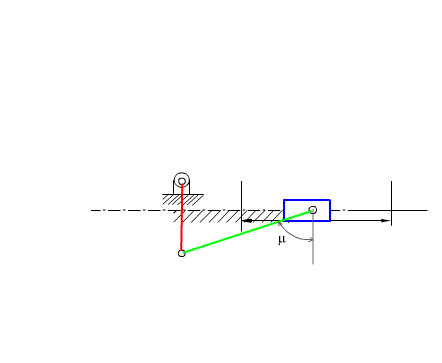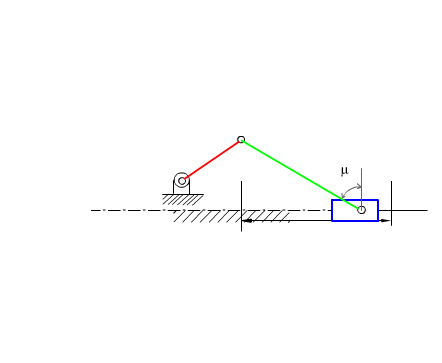
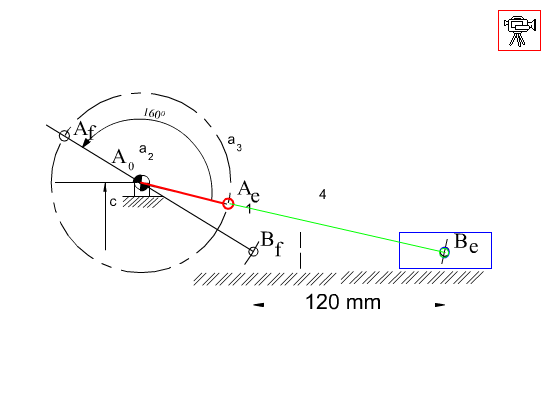
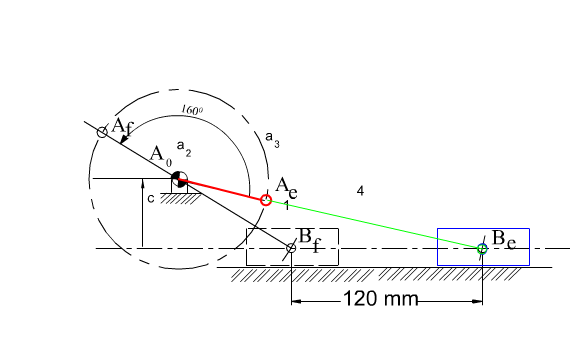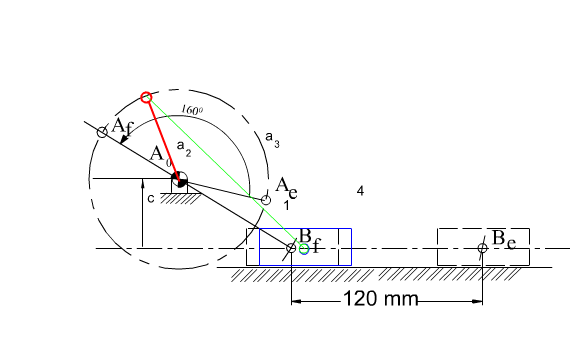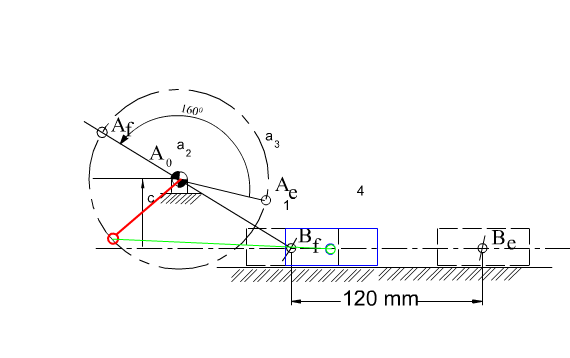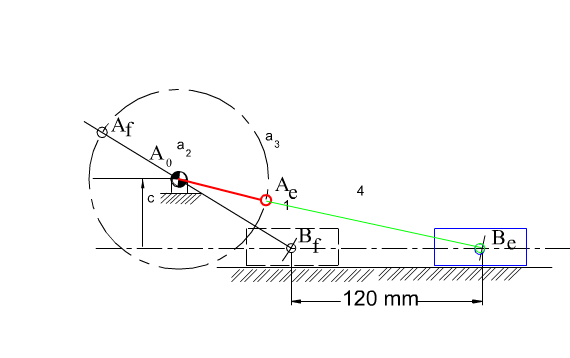
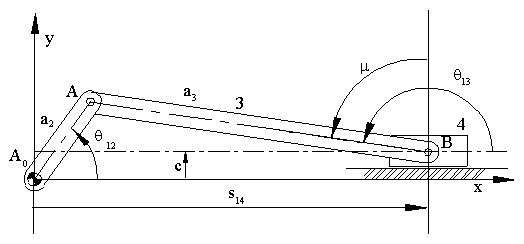
Another mechanism that has a very wide usage in machine design is the slider-crank mechanism. It is mainly used to convert rotary motion to a reciprocating motion or vice versa. Below a slider-crank mechanism is shown and the parameters that are used to define the angles and the link lengths are given. As in the four-bar mechanism, the extended and folded dead centre positions are when the crank and the coupler are collinear (coupler link is commonly called connecting rod in slider-crank mechanisms). Full rotation of the crank is possible if the eccentricity, c, is less than the difference between the connecting rod and the crank lengths and the crank length is less than the connecting rod length (e.g. c < (a₃ – a₂) and a₃ > a₂) .

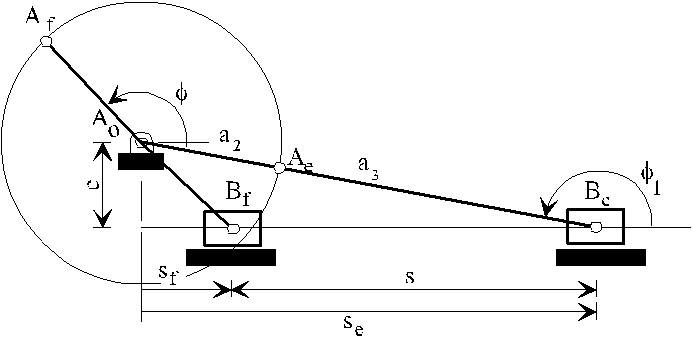
Using the right angled triangles formed at the dead-center positions:

$\displaystyle \text{s}_\text{e}=\sqrt{{{{{\left( {{\text{a}}_{2}+{\text{a}}_{3}} \right)}}^{2}}-{{\text{c}}^{2}}}}$

$\displaystyle \text{s}_\text{f}=\sqrt{{{{{\left( {{\text{a}}_{2}-{\text{a}}_{3}} \right)}}^{2}}-{{\text{c}}^{2}}}}$

Noting s = s_e – s_f = stroke = the distance slider travels between dead-centres. If we let λ = a₂/a₃ and e = c/a₃, the stroke will be given by:

$\displaystyle \text{s}={{\text{a}}_{3}}\sqrt{{{{{\left( {1+\text{λ}} \right)}}^{2}}-{{\text{ε}}^{2}}}}-{{\text{a}}_{3}}\sqrt{{{{{\left( {1-\text{λ}} \right)}}^{2}}-{{\text{ε}}^{2}}}}$

If the eccentricity, c (or a₁), is zero (c = 0) the slider crank mechanism is called an in-line slider-crank and the stroke is twice the crank length (s = 2a₂). If the eccentricity is not zero (c ≠ 0), it is usually called an offset slider-crank mechanism.

The transmission angle can be determined from the equation:

a₃cosμ = a₂sinθ₁₂ − c

(1)

Maximum deviation of the transmission angle occurs when the derivative of μ with respect to q₁₂ is zero. Hence differentiating equation (1) with respect to q₁₂:

\displaystyle \frac{{\text{dμ}}}{{\text{d}{{\text{θ}}_{{12}}}}}=\frac{{-\cos {{θ}_{{12}}}}}{{\sin \text{μ}}}=0

(2)

Maximum or minimum deviation occurs when q₁₂ is 90° or 270° (see figure below) and the value of the maximum or minimum transmission angle is given by:

\displaystyle \cos {{\text{μ}}_{\begin{smallmatrix} \text{max} \\ \text{min} \end{smallmatrix}}}=\frac{{-\text{c}\pm {{\text{a}}_{2}}}}{{{{\text{a}}_{3}}}}

(3)

If c is positive as shown below, transmission angle is critical when q₁₂ = 270°. If c is negative, then the most critical transmission angle is at q₁₂ = 90°.

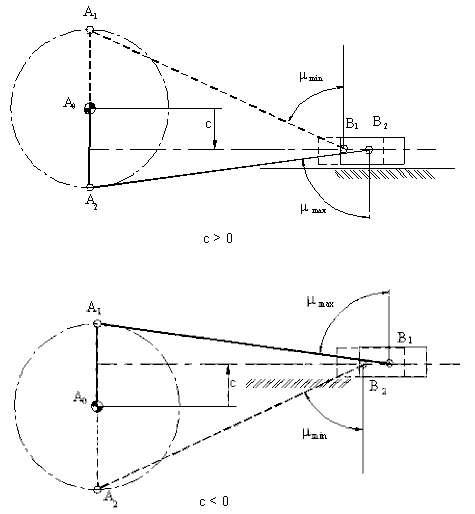
If the eccentricity, c, is zero, maximum value of the transmission angle is given by:

\displaystyle \cos {{\text{μ}}_{\begin{smallmatrix} \text{max} \\ \text{min} \end{smallmatrix}}}=\pm \frac{{{\text{a}}_{2}}}{{{\text{a}}_{3}}}

(4)

In reciprocating pumps, the crank-to-connecting rod ratio is kept less than 1/4, which corresponds to 14.48° maximum deviation of the transmission angle from 90°. Since the crank length is fixed by the required stroke (a₂ = s/2) one must increase the connecting-rod length for better transmission angles. However, this will increase the size of the mechanism.

Similar to the transmission angle problem in the four-bar mechanisms, the transmission angle problem in slider-crank mechanisms can be stated as follows:

Determine the slider-crank proportions with a given stroke, s, and corresponding crank rotation between dead-centers, ϕ, such that the maximum deviation of the transmission angle from 90° is a minimum.

The problem can again be considered in two parts. The first part is the determination of slider crank mechanisms with a given stroke and corresponding crank rotation. The second part is the determination of one particular slider-crank mechanism with optimum transmission angle variation.

For the first part of the problem note that the stroke s is a function of the link length ratios, i.e. if we double the length of the links, the stroke will be doubled. Therefore without loss of generality, let s = 1 (the link lengths thus found will be multiplied by the stroke to give the actual values).

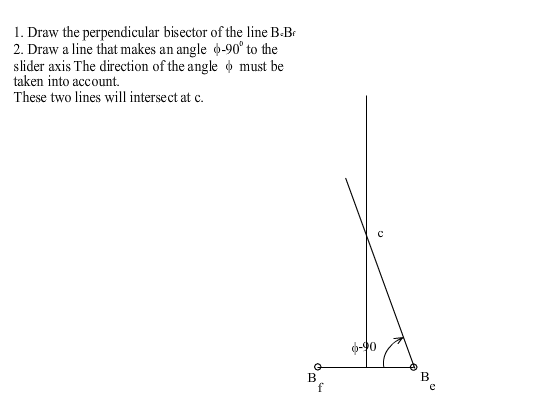
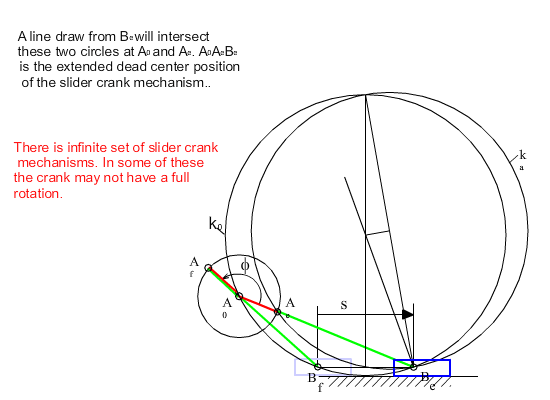
Referring to the figure where the slider crank mechanism is drawn at its dead centers, the loop closure equations at the dead-centers are:

A₀B_e + B_eA_e + A_eA₀ = 0	(5)
A₀B_f + B_fA_f + A_fA₀ = 0	(6)

or in complex numbers:

ic + s_e + (a₃ + a₂)e^iϕ₁ = 0	(7)
ic + s_e + (a₃ − a₂)e^{i(ϕ₁+ϕ−π)} = 0	(8)

Subtracting equation (8) from equation (7) and noting that s_e − s_f = s = 1:

1 + (a₃ + a₂)e^iϕ₁ + (a₃ − a₂)e^i(ϕ₁+ϕ) = 0

(9)

If we let Z = a₃e^iϕ₁ and λ = a₂/a₃ equation (8) can be rewritten in the form:

(1 + λ)Z + (1 − λ)e^iϕZ + 1 = 0

(10)

For a full rotation of the crank a necessary (but not sufficient) condition is λ < 1. Equation 10 can be solved for Z to yield:

Z =

\displaystyle \frac{{-1}}{{1+{{\text{e}}^{{\text{iϕ}}}}+\text{λ}\left( {1-{{\text{e}}^{{\text{iϕ}}}}} \right)}}

(11)

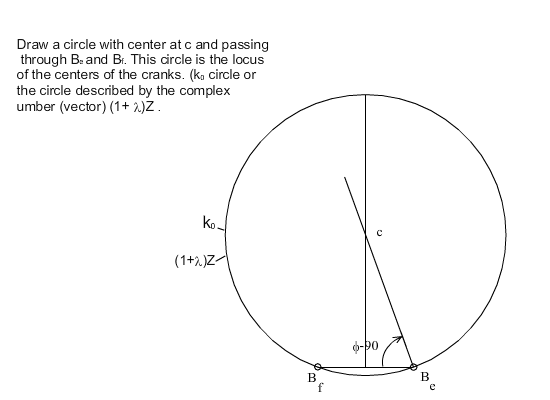
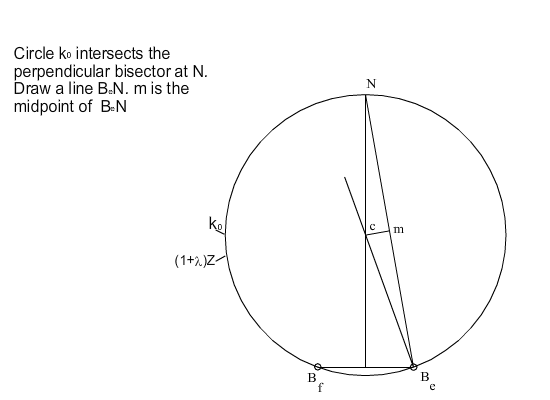
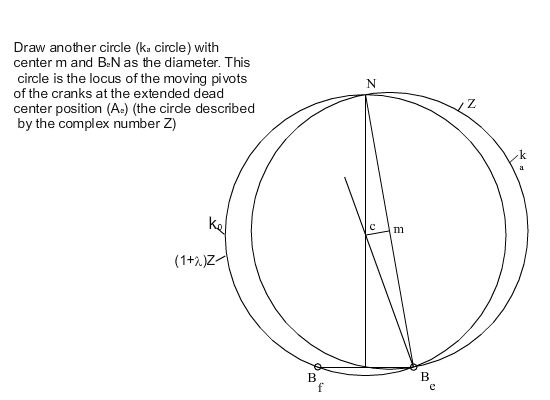
If λ is taken as a free parameter, as it varies, the tip of Z given by (7), will generate a circle which is the locus of all possible moving pivots for the crank when the crank and the coupler are at extended position (k_a circle). The locus of all possible fixed pivots is another circle (k₀ circle) which is given by Z(1 + λ) (the origin for both vectors is B_e with the real axis parallel to the slider axis). Any line drawn from B_e intersects these circles at A_e and A₀ respectively, yielding the slider-crank mechanism in extended dead-center position. Below these circles are shown for ϕ = 160°.

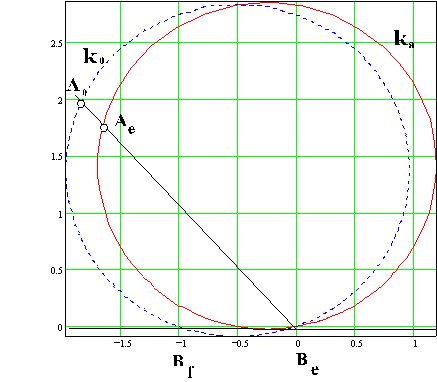
The eccentricity, c can be obtained as the imaginary component of the vector B_eA₀ = B_eA_e + A_eA₀ which can be written as:

2ic = (a₃ + a₂)e^iϕ₁ − (a₃ + a₂)e^−iϕ₁ = 0

(12)

or using Z and λ:

2ic = Z(1 + λ) −

\displaystyle {{\bar{\text{Z}}}}

(1 + λ)

(13)

and substituting the value of Z:

$\displaystyle \text{c}=\frac{1}{2}\frac{{\left( {1-{{\text{λ}}^{2}}} \right)\sin \text{ϕ}}}{{1+{{\text{λ}}^{2}}+\left( {1-{{\text{λ}}^{2}}} \right)\cos \text{ϕ}}}$	(14)
The link lengths can now be expressed as: $\displaystyle {{\text{a}}_{3}}^{2}=\frac{1}{2}\frac{1}{{1+{{\text{λ}}^{2}}+\left( {1-{{\text{λ}}^{2}}} \right)\cos \text{ϕ}}}=\frac{1}{4}\frac{1}{{{{{\cos }}^{2}}\left( {\text{ϕ}/2} \right)+{{\text{λ}}^{2}}{{{\sin }}^{2}}\left( {\text{ϕ}/2} \right)}}$	(15)
$\displaystyle {{\text{a}}_{2}}^{2}={{\text{λ}}^{2}}{{\text{a}}_{3}}^{2}=\frac{1}{2}\frac{{{{\text{λ}}^{2}}}}{{1+{{\text{λ}}^{2}}+\left( {1-{{\text{λ}}^{2}}} \right)\cos \text{ϕ}}}=\frac{1}{4}\frac{{{{\text{λ}}^{2}}}}{{{{{\cos }}^{2}}\left( {\text{ϕ}/2} \right)+{{\text{λ}}^{2}}{{{\sin }}^{2}}\left( {\text{ϕ}/2} \right)}}$	(16)

Equations (14-16) yield a singly infinite set of solutions for the slider-crank mechanisms satisfying a given crank rotation (stroke = 1 unit). One can also use the eccentricity, crank or coupler link length as the free parameter to determine the other link lengths.

For the Geometric Solution:

Example:

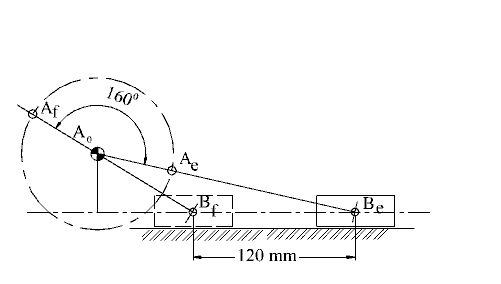
Determine the link lengths of the slider crank mechanism with a stoke s = 120 mm, corresponding crank rotation ϕ = 160° and the crank to coupler link ratio λ = 0.5.

Using unit stroke, from equations (14), (15) and (16) the link lengths are:

a₂ = 0.47881, a₃= 0.95762 and c = 0.23523. For s = 120:

a₂ = 114.91mm, a₃ = 57.46mm and c = 28.23mm.

The minimum transmission angle for this mechanism is m_min = 41.79°.

Determine the link lengths of the slider-crank mechanism having the same stoke and corresponding crank rotation as in the first example, but instead of crank to coupler link ratio specified, the eccentricity is specified as c = 20 mm.

For unit stroke c = 20/120 = 0.16667. Solving equation (10) for λ yields:

\displaystyle {{\text{λ}}^{2}}=\frac{{1-2\text{c}\cot \left( {\text{ϕ}/2} \right)}}{{1+2\text{c}\tan \left( {\text{ϕ}/2} \right)}}

(17)

For c = 0.16667, λ² = 0.325635. Substituting into equations (15) and (16), a₂ = 0.48508 and a₃ = 0.85006. For s = 120 mm, c = 20 mm, a₂ = 58.21 mm and a₃ = 102.01 mm. The minimum transmission angle for this mechanism is μ_min = 39.94°. Note that a similar procedure can be carried out if crank or coupler link length is specified.

The minimum transmission angle is when θ = p/2:

μ_min = cos^-1

\displaystyle \left( {\frac{{\text{c}+\text{a}}}{\text{b}}} \right)

(18)

For the full rotatability of the crank, c + a₂ < a₃ or c < a₃ – a₂. At the limit position (c = a₃ – a₂), m_min = 0. Using equations (14), (15) and (16) this condition yields the limits of ϕ for crank rotatability as:

π/2 ≤ ϕ ≤ tan^-1(−1/c)

(19)

and cot²(ϕ/2) < λ < 1.

Expressing μ_min in terms of λ and ϕ (substitute equations 14, 15 and 16 into equation 18 and simplify):

\displaystyle \cos {{\text{μ}}_{{\text{min}}}}=\text{λ}+\frac{1}{2}\frac{{\left( {1-{{\text{λ}}^{2}}} \right)\sin \text{ϕ}}}{{\sqrt{{1+{{\text{λ}}^{2}}+\left( {1-{{\text{λ}}^{2}}} \right)\cos \text{ϕ}}}}}

(20)

since λ is a free design parameter, the necessary condition for the minimum transmission angle to be a maximum is dμ_min/dλ = 0

If the value of λ which makes the derivative equal to zero is λ = λ_opt, differentiating equation (20) and setting dμ_min/dλ = 0 yields.

t²Q³ + (1 − t²)Q² − (1 + t² + t⁴)Q + 1 + t² = 0

(21)

where Q = λ²_optt² and t = tan(ϕ/2). The roots of equation (21) are:

\displaystyle {{\text{Q}}_{1}}=-\frac{1}{2}+\frac{1}{2}\sqrt{{5+4{{\text{t}}^{2}}}}

;

\displaystyle {{\text{Q}}_{2}}=-\frac{1}{2}-\frac{1}{2}\sqrt{{5+4{{\text{t}}^{2}}}}

;

\displaystyle {{\text{Q}}_{3}}=-\frac{1}{{{{\text{t}}^{2}}}}

(22)

Since Q must be positive, Q₂ is not a solution. Corresponding to Q₃, λ = 1/t², the deviation of the minimum transmission angle 90° is maximized (cosμ_min = 1). The root Q₁ yields the value of λ_opt within the range (1/t², λ), and this value satisfies the necessary and sufficient condition for slider-crank mechanism with optimum transmission angle characteristics. Therefore:

\displaystyle {{\text{λ}}_{{\text{opt}}}}^{2}=\frac{{\sqrt{{5+4{{\text{t}}^{2}}}}-1}}{{2{{\text{t}}^{2}}}}

(23)

is the unique optimum solution.

Example:

For slider stroke s = 120 mm and corresponding crank rotation ϕ = 160°, determine the slider crank mechanism with optimum force transmission characteristics.

From equation (20), λ_opt = 0.405185. Utilising equations (14), (15) and (16) for unit stroke the link lengths are a₂ = 0.465542 ; a₃ = 1.14896 ; c = 0.377378 and for 120 mm stroke:

a₂ = 55.87 mm, a₃ = 137.88 mm, c = 42.81 mm

The minimum transmission angle for the mechanism is m_min = 42.81°.

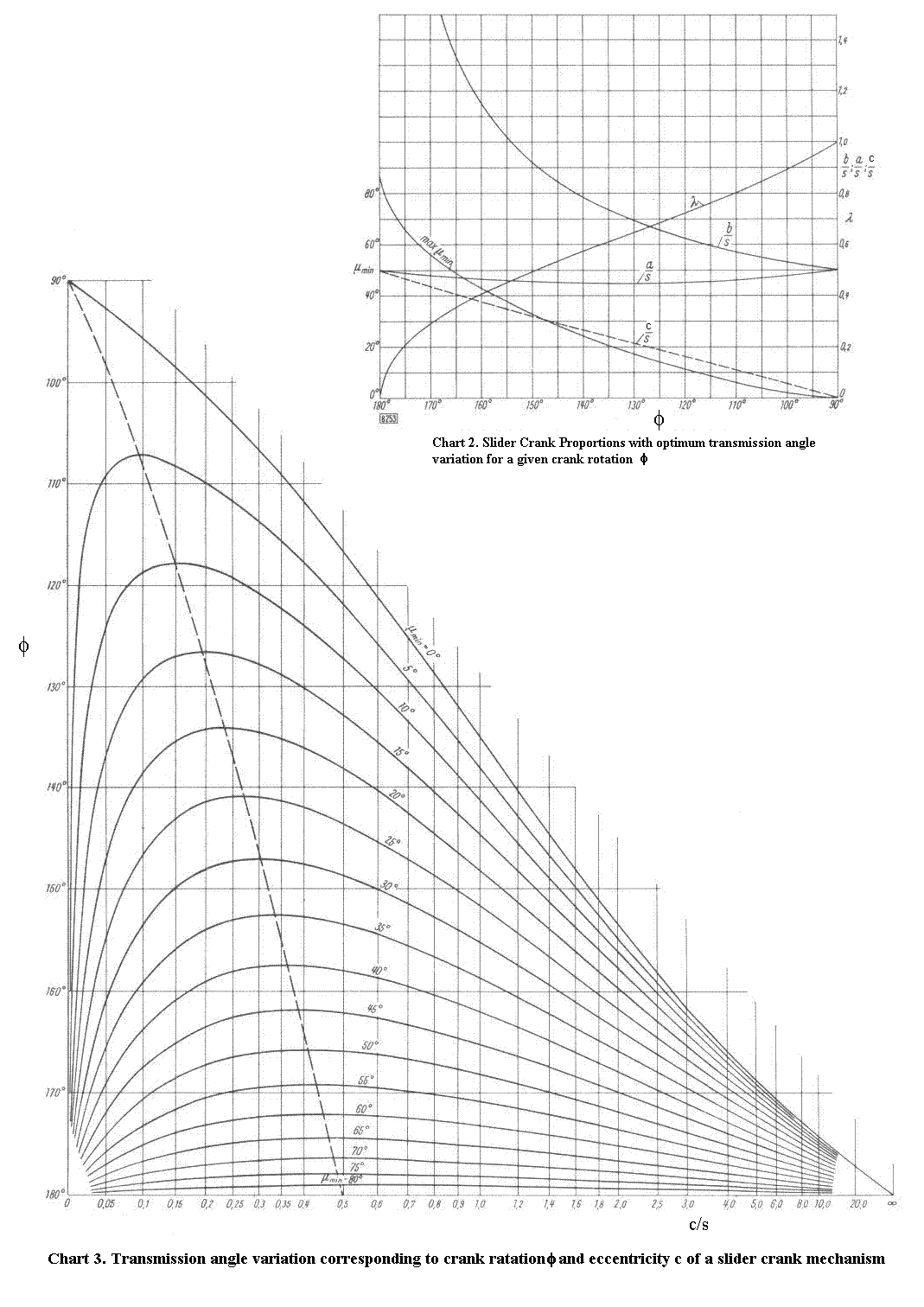
The results are given in Chart 2. The slider-crank link lengths (a₂, a₃, c) and optimum values and the minimum transmission angle μ_min as a function of crank rotation between dead centers is given. In Chart 3, all possible solutions and their minimum transmission angle values are given (note that the horizontal axis is not with a linear scale).