6.4. DYNAMIC FORCE ANALYSIS OF MACHINERY

h is given by: h = T_G3ⁱ/F₃ⁱ = 33.31 mm.

For the force analysis we proceed as if the inertia forces were external forces and apply the methods that were described before for force analysis.

Graphical Method:

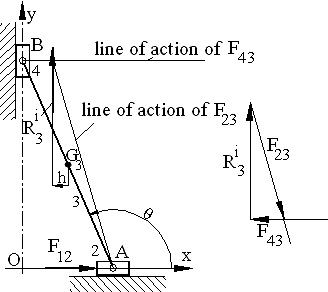
Link 4 is a two force, link 3 and link 2 are three force members.and. For link 3, since R₃ⁱ is known, we determine the point of concurrency of the three forces and draw the force polygon for the equilibrium equation R₃ⁱ + F₂₃ + F₄₃ = 0 as shown in the figure. For link 4, G₁₄ = –F₃₄ = F₄₃. For link 2, F₃₂ + F₁₂ + G₁₂ = 0. Since F₃₂ = –F₂₃, the force polygon for the equilibrium equation is that drawn for link 3 with all the arrows reversed. Hence G₁₂ = –R₃ⁱ and F₁₂ = –F₄₃.

Analytical Method

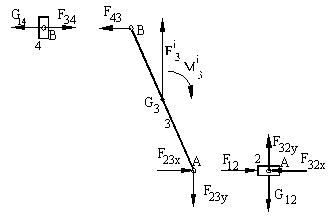
In the analytical method, since the moment and force equilibrium equations are going to be used separately, one needs not combine the inertia force and torque into a single resultant. The free body diagrams of the moving links are as shown in the above figure.

Since:

  F₄₃ = F₄₃ ∠180°

  F₃ⁱ = 25.97 N ∠90°

For link 3 the equilibrium equations are:

F₄₃ – F_23x = 0

F₃ⁱ – F_23y = 0

and the moment equilibrium about point A is:

     500 F₄₃ sin(180° – 113.578°) + 250 (25.97) sin(90° – 113.578°) – 865 = 0

or

    458.258 F₄₃ = 3461.981

F₄₃ = 7.555 N ∠180°                  F₃₂= –F₂₃ = 27.04 N ∠106.22°

F_23x = 7.555 N ∠0°                     F₁₂ = 7.555 N ∠0°

F_23y = 25.97 N ∠270°                 G₁₂ = 25.97 N ∠270°

F₂₃ = 27.04 N ∠–73.78°             G₁₄ = F₄₃

6.4.1. Dynamic Force Analysis of a Four-Bar Mechanism

In order to design links and joints one must determine the worst loading conditions of each link and joint. In order to select the driving motor characteristics, input torque for the whole cycle is required. In such cases analytical methods suitable for numerical computation is utilized. In this part a general dynamic analysis of a four-bar mechanism will be explained and the results will be applied to a particular four-bar for a complete force analysis.

Referring to the figure, the equations for the position, velocity and acceleration analysis of the four-bar mechanism are:

Position Analysis

r cosϕ = a₁ cosθ₁₂ – a₁

r sinϕ = a₁ sinθ₁₂

λ = cos^-1 \displaystyle \left(\frac {{\text{a}_4}^2+{\text{r}}^2-{\text{a}_3}^2}{2\text{a}_4\text{r}}\right)

μ = cos^-1 \displaystyle \left(\frac {{\text{a}_3}^2+{\text{a}_4}^2-{\text{r}}^2}{2\text{a}_3\text{a}_4}\right)

θ₁₄ = ϕ – σλ

θ₁₃ = θ₁₄ – σμ

Note that rcosf and rsinf terms must be solved for r and f simultaneously and the correct quadrant must be ensured. The term s = ±1 depending on whether the mechanism is of open or cross configuration.

Velocity Analysis:

\displaystyle {{\text{ω}}_{{13}}}=\frac{{{{\text{a}}_{2}}}}{{{{\text{a}}_{3}}}}\frac{{\sin \left( {{{\text{θ}}_{{12}}}-{{\text{θ}}_{{14}}}} \right)}}{{\sin \left( {{{\text{θ}}_{{14}}}-{{\text{θ}}_{{13}}}} \right)}}{{\text{ω}}_{{12}}}

\displaystyle {{\text{ω}}_{{14}}}=\frac{{{{\text{a}}_{2}}}}{{{{\text{a}}_{4}}}}\frac{{\sin \left( {{{\text{θ}}_{{12}}}-{{\text{θ}}_{{13}}}} \right)}}{{\sin \left( {{{\text{θ}}_{{14}}}-{{\text{θ}}_{{13}}}} \right)}}{{\text{ω}}_{{12}}}

Acceleration  Analysis

\displaystyle {{\text{α}}_{{13}}}=\frac{{{{\text{a}}_{2}}{{\text{α}}_{{12}}}\sin \left( {{{\text{θ}}_{{12}}}-{{\text{θ}}_{{14}}}} \right)+{{\text{a}}_{2}}{{\text{ω}}_{{12}}}^{2}\cos \left( {{{\text{θ}}_{{12}}}-{{\text{θ}}_{{14}}}} \right)+{{\text{a}}_{3}}{{\text{ω}}_{{13}}}^{2}\cos \left( {{{\text{θ}}_{{13}}}-{{\text{θ}}_{{14}}}} \right)-{{\text{a}}_{4}}{{\text{ω}}_{{12}}}^{2}}}{{{{\text{a}}_{3}}\sin \left( {{{\text{θ}}_{{14}}}-{{\text{θ}}_{{13}}}} \right)}}

\displaystyle {{\text{α}}_{{14}}}=\frac{{{{\text{a}}_{2}}{{\text{α}}_{{12}}}\sin \left( {{{\text{θ}}_{{12}}}-{{\text{θ}}_{{13}}}} \right)+{{\text{a}}_{2}}{{\text{ω}}_{{12}}}^{2}\cos \left( {{{\text{θ}}_{{12}}}-{{\text{θ}}_{{13}}}} \right)+{{\text{a}}_{3}}{{\text{ω}}_{{13}}}^{2}-{{\text{a}}_{4}}{{\text{ω}}_{{14}}}^{2}\cos \left( {{{\text{θ}}_{{13}}}-{{\text{θ}}_{{14}}}} \right)}}{{{{\text{a}}_{4}}\sin \left( {{{\text{θ}}_{{14}}}-{{\text{θ}}_{{13}}}} \right)}}

The above equations can be written in different forms.

Acceleration of the centers of gravity

a_G2x = −g₂ω₁₂²cos(θ₁₂ + β₂) − g₂α₁₂sin(θ₁₂ + β₂)

a_G2y = −g₂ω₁₂²sin(θ₁₂ + β₂) + g₂α₁₂cos(θ₁₂ + β₂)

a_G3x = −a₂ω₁₂²cosθ₁₂ − a₂α₁₂sinθ₁₂ − g₃ω₁₃²cos(θ₁₃ + β₃) − g₃α₁₃sin(θ₁₃ + β₃)

a_G3y = −a₂ω₁₂²sinθ₁₂ + a₂α₁₂cosθ₁₂ − g₃ω₁₃²sin(θ₁₃ + β₃) + g₃α₁₃cos(θ₁₃ + β₃)

a_G4x = −g₄ω₁₄²cos(θ₁₄ + β₄) − g₄α₁₄sin(θ₁₄ + β₄)

a_G4y = −g₄ω₁₄²sin(θ₁₄ + β₄) + g₄α₁₄cos(θ₁₄ + β₄)

Using the above equations, one can determine the angular acceleration of the links and the linear accelerations of the centers of gravity for any input condition (input position, velocity and acceleration).

For dynamic force analysis in addition of the inertia forces, we shall assume known external forces F₁₃ and F₁₄ acting on links 3 and 4 and an unknown torque, T₁₂ acting on link 2 as shown in the figure. The system is in dynamic equilibrium under the action of these forces. We would like to determine the input torque and the joint reaction forces.

Note that:

   F₂ⁱ = −m₂a_G2 ,   F₃ⁱ = −m₃a_G3,  F₄ⁱ = −m₄a_G4  and  T₂ⁱ = −I_G2α₁₂ , T₃ⁱ = −I_G3α_G3 , T₄ⁱ = −I_G4α₁₄

The free body diagrams of each moving link can be drawn and the equilibrium equations can be written:

For link 4:

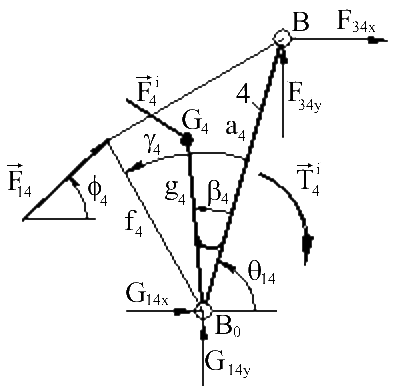
F34x + G14x + F14cosϕ4 − m4aG4x = 0	(1)
F34y + G14y + F14sinϕ4 − m4aG4y = 0	(2)
F34ya4sin(π/2 − θ14) + F34xa4sin(−θ14) + F14f4sin(ϕ4 − θ14 − γ4) − I4α14 − m4aG4xg4sin(−θ14 − β4) − m4aG4yg4sin(π/2 − θ14 − β4) = 0	(3)

For link 3:

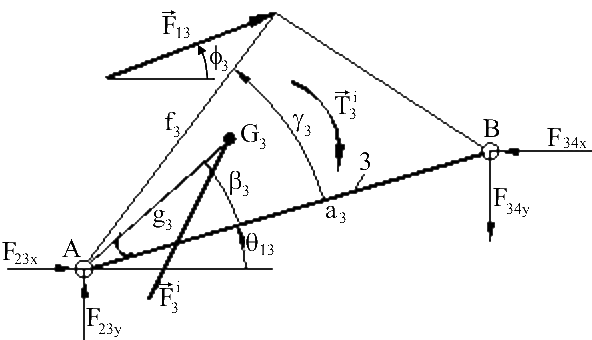
F23x − F34x + F13cosϕ3 − m3aG3x = 0	(4)
F23y − F34y + F13sinϕ3 − m3aG3y = 0	(5)
F34xa3sin(π − θ13) + F34ya3sin(−π/2 − θ13) + F13f4sin(ϕ3 − θ13 − γ3) − I3α13 − m3aG3xg3sin(−θ13 − β3) − m3aG3yg3sin(π/2 − θ13 − β3) = 0	(6)

For link 2:

−F23x + G12x − m2aG2x = 0	(7)
−F23y + G12y − m2aG2y = 0	(8)
F23xa2sin(π − θ12) + F23ya2sin(−π/2 − θ12) + T12 − I2α12 − m2aG2xg2sin(−θ12 − β2) − m2aG2yg2sin(π/2 − θ12 − β2) = 0	(9)

Hence, we obtain nine linear equations in nine unknowns (G_14x,  G_14y, F_34x, F_34y, F_23x, F_23y, G_12x, G_12y and T₁₂). If a computer subroutine for the matrix solution is available, these equations can be solved directly for the unknowns. However, it is much simpler to solve equations (3) and (6) simultaneously for F_34y and F_34x and then solve for each unknown from the remaining equations. The solution is as follows:

A = I₄α₁₄ + m₄g₄[a_G4y cos(θ₁₄ + β₄) − a_G4xsin(θ₁₄ + β₄)] − F₁₄f₄sin(ϕ₄ − θ₁₄ − γ₄)

  B = I₃α₁₃ + m₃g₃[a_G3y cos(θ₁₃ + β₃) − a_G3xsin(θ₁₃ + β₃)] − F₁₃f₃sin(ϕ₃ − θ₁₃ − γ₃)

  F_34x = [Aa₃cosθ₁₃ + Ba₄cosθ₁₄]/[a₃a₄sin(θ₁₃ − θ₁₄)]

  F_34y= [Aa₃sinθ₁₃ + Ba₄sinθ₁₄]/[a₃a₄sin(θ₁₃ − θ₁₄)]

  G_14x = −F_34x + m₄a_G4x − F₁₄cosϕ₄

  G_14y = −F_34y + m₄a_G4y − F₁₄sinϕ₄

  F_23x = F_34x + m₃a_G3x − F₁₃cosϕ₃

  F_23y = F_34y + m₃a_G3y − F₁₃sinϕ₃

 G_12x = F_23x + m₂a_G2x

  G_12y = F_23y + m₂a_G2y

T₁₂ =  F_23ya₂cosθ₁₂ − F_23xa₂sinθ₁₂ + I₂α₁₂  + m₂g₂[a_G2ysin(θ₁₂ + β₂) − a_G2xsin(θ₁₂ + β₂)]

One can as well use the principle of superposition and consider forces acting on each link at one time and later add all the force components to find the resultant joint forces. The equations thus found will be similiar to the ones obtained above (written in a different form). This is left as an exercise.

Example:

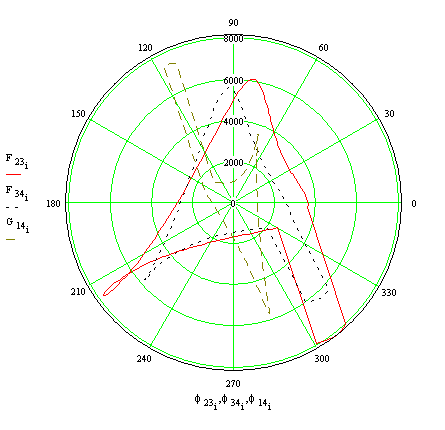
The four-bar mechanism shown in is used to cut running strip of material. The input link is rotating at a constant speed of 900 rpm CCW. The link dimensions are: |A₀A| = 85 mm, |AB| = 235 mm, |B₀B| = 550 mm, |BC| = 238 mm, |AC| = 467 mm, |B₀C| = 487 mm, ∠BAC₃ = 7.6°, ∠BB₀C₄ = 25.6°. Using AutoCad solid modeller, the mass properties for links 3 and 4 are found as m₃ = 2 kg, k₃ = 268 mm (radius of gyration), |AG₃| = 231 mm, ∠BAG₃ = 1° (CW), m₄ = 5.1 kg, k₄ = 424 mm, |B₀G₄| = 305 mm, ∠BB₀G₄ = 7° (CW). For link 2, m₂ = 3 kg,  k₂ = 100 mm and its center of mass is coincident with A₀. We are to determine the required input torque and the joint reaction forces. We can neglect friction. A cutting force of 2000 N acts vertically on both links 3 and 4 at point C when the crank angle is 124° < θ₁₂ < 156°. MathCad solution for this example is as follows:

Link dimensions:

           

          

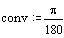
Constant speed is assumed:

       

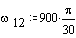
Increment crank angle for every 2 degrees:

     

m is crank angle in degrees. Solve for position variables:

             

                

           

                               

             

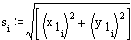
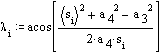
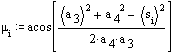
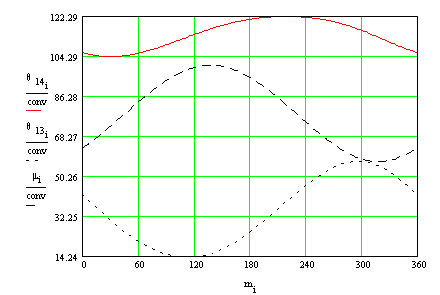
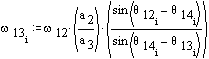
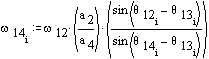
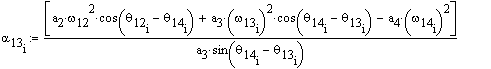
The angular speed and acceleration of the links are as follows: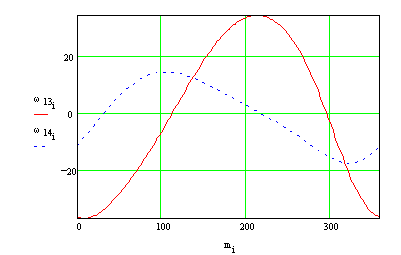

Acceleration of the centers of mass of the links (in mm/s²):

                                  

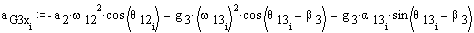
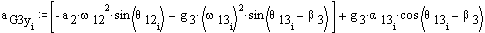
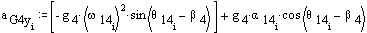
Mass properties (mass in kg and the radii of gyration, k_i, in mm):

                                                      

This constant C is to be used to convert mm to m (note that 1kg m/s² = 1 N). The external forces:

                        

This external force will act vertically on both links 3 and 4 in opposite direction.Determine the joint forces and the input torque (note that the joint forces are in Newtons and the torque is in Newton-meters):

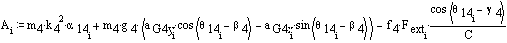
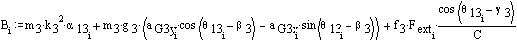
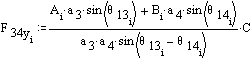
Input torque as a function of crank angle:

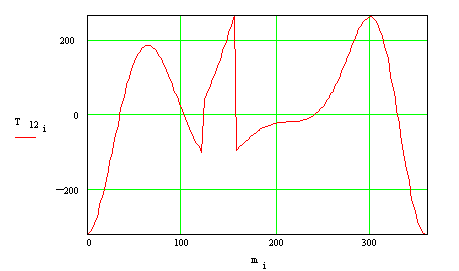
Convert the forces to polar form and plot the forces in a polar plot:
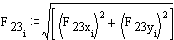
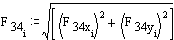