4.2 VELOCITY AND ACCELERATION ANALYSIS OF MECHANISMS-4
Example:
Mechanism shown in the figure is used in a hay bailing machine. We are to determine the velocity and acceleration of point F on link 6 when the input link is rotating at a constant velocity of 4 rad/s. The link lengths are as given on the figure.
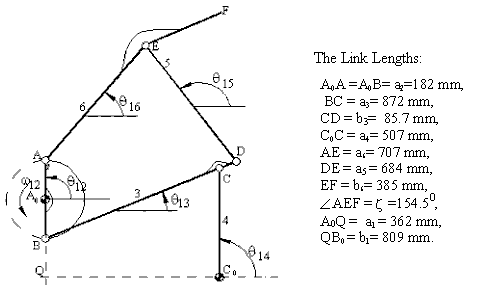
In this problem, for the position analysis stepwise solution and for the velocity and acceleration analysis matrix inversion method will be used.
Define the fixed link lengths:
ω12 := 4 
Generate the input crank angle for every 5°:
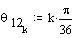
xBk, yBk are the rectangular coordinates of B with respect to C0 with x-axis along QC0.
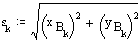
Convert rectangular coordinates to polar coordinates.
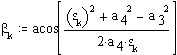Cosine theorem for angle BC0C.
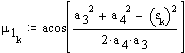Cosine theorem for the transmission angle BCC0
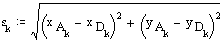
Note that ϕ, β and s are used as dummy variables.
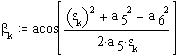
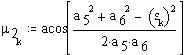
x numbers with A0 as the origin.
Coordinates of F in complex numbers:
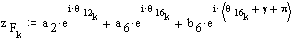
In figure below, the path of point F is shown (the x sign is the position of point F when θ12 = 90°).
For velocity and acceleration analysis create the coefficient matrix:
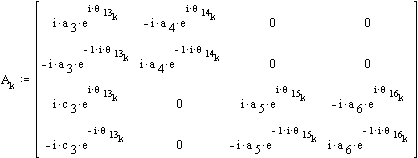
The angular velocities are found from the velocity loop equations.
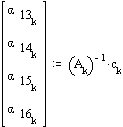
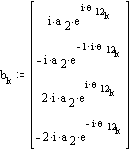
The angular acceleration of the links are found from the acceleration loop equations.
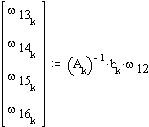
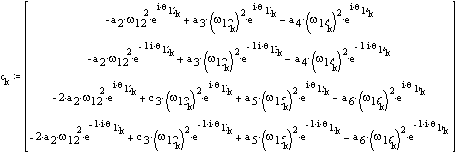
Velocity and acceleration of point F:
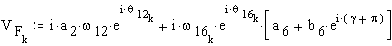
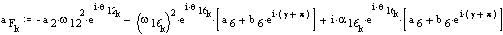
The polar plots of the velocity and acceleration vectors of point F for a complete cycle are shown below (velocity values are measured in mm/s).
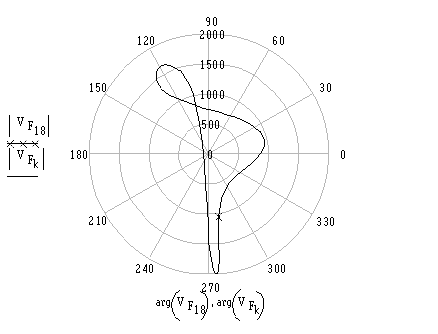(Velocity of F at an instant is the vector from point 0 to a point on the curve; e.g. velocity of Point F when θ12 = 90° is the line drawn from 0 to the mark x)
The polar plots of the velocity and acceleration vectors of point F for a complete cycle are shown below (acceleration values are measured in mm/s2).
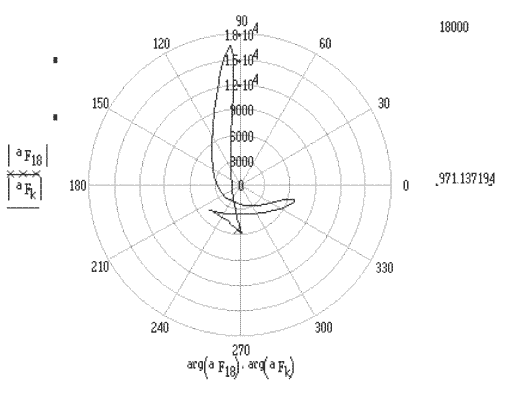
(Acceleration of F at an instant is the vector from point 0 to a point on the curve; e.g. acceleration of Point F when θ12 = 90° is the line drawn from o to the mark x)
In case of graphical solution for the position given, link 2 is in a fixed axis of rotation with ω12 = 4 rad/s. Therefore vA = vB = 728 mm/s and while vA is to the left, vB is to the right. Using a scale factor kv =0.5 mm/(mm/s) we draw these known vectors (see figure). Considering the loop formed by links 1, 2, 3 and 4, the velocity equation is:
vC = vB + vC/B
vC/B is perpendicular to CB and vC is perpendicular to CC0. At the given position, since BA0 and CC0 are parallel, vC and vB must be equal and vC/B = 0 and ω13 = 0. In such a case vD = vC = vB. Next, consider point E which is a permanently coincident point on links 5 and 6. For points D and E on link 5:
vE = vD + vE/D
Similarly, for points A and E on link 6:
vE = vA + vE/A
vD and vAare of known magnitude and direction. The relative velocities vE/D and vE/A must be perpendicular to ED and EA respectively. Although these two equations cannot be solved separately, when they are equated to each other, the two relative velocity magnitudes are the unknowns. Therefore simultaneous solution is made. For the velocity of point F, we can apply Mehmke’s theorem or solve the two vector equations
vF = vE + vF/E
vF = vA + vF/A
simultaneously.
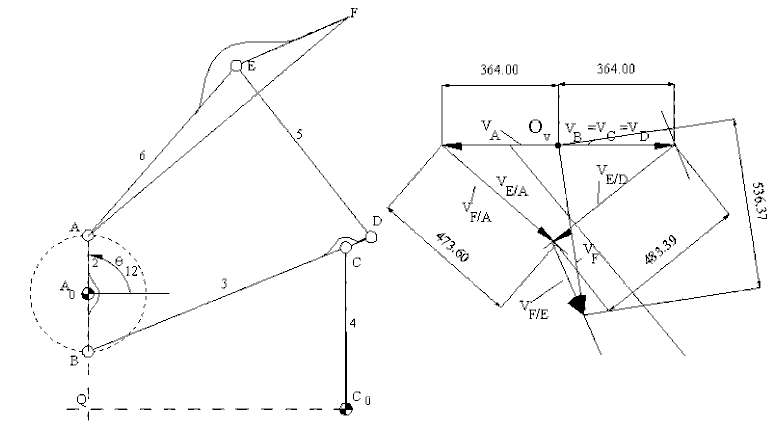
Velocity Polygon
For the acceleration analysis we use the same points that have been used for the velocity analysis. However we have to write the acceleration of these points in terms of their components. Since link 2 is rotating at a constant speed, the tangential accelerations of points A and B are zero (aA = anA, aB = anB). aA = aB = 2912 mm/s2, both towards the center of rotation. Using a scale factor ka = 0.2 mm/(mm/s2), we draw these vectors (see figure). Next we write the acceleration of point C as:
anC + atC = anB + anC/B + atC/B
anC is a vector along CC0 towards C0 and is of magnitude |CC0|ω132 = vC2/|CC0|= 1045 mm/s2. anC/B = 0 since ω13 = 0 for this position. atC and atC/B are perpendicular to CC0 and CB, respectively (unknown magnitudes). Note that while ω13 = 0, α13 ≠ 0. atD/B can now be determined since α13 = atC/B /|CB| (anD/B = 0). Hence aD is known. For point E we can write:
aE = aD + anE/D + atE/D
and
aE = aA + anE/A + atE/A
anE/D = |ED|ω152 = vE/D2/|ED| = 1366 mm/s2 (along ED, towards D)
anE/A = |EA|ω162 = vE/A2/|EA| = 1269 mm/s2 (along EA, towards A)
Tangential acceleration components atE/D and atE/A are perpendicular to the lines ED and EA respectively (unknown magnitudes). The two equations can now be solved simultaneously to determine the velocity of point E. For the acceleration of point F, Mehmke’s theorem is applied (triangle aef on the acceleration polygon is similar to the triangle AEF of link 6). The result is shown in the figure below. Hence aF = 1075.5/0.2 =5378 mm/s2 , downwards as shown.
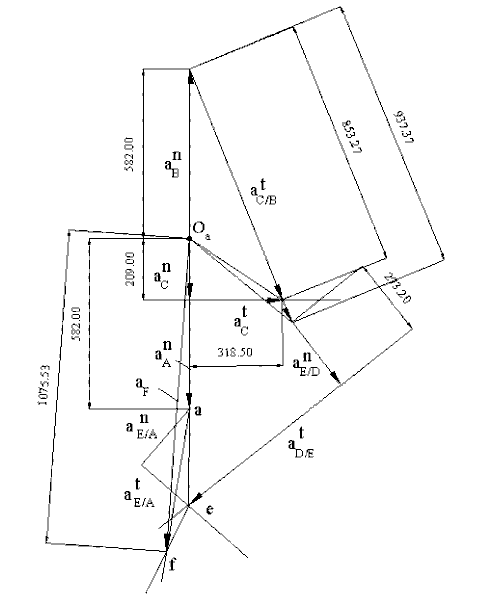
Acceleration Polygon
