4.2 VELOCITY AND ACCELERATION ANALYSIS OF MECHANISMS-1

Velocity and acceleration analysis of mechanisms can be performed vectorially using the relative velocity and acceleration concept. Usually we start with the given values and work through the mechanism by way of series of points A, B, C, etc. Solving vector equations in the form:

v_B = v_A + v_B/A

v_C = v_B + v_C/B

etc. for velocity and

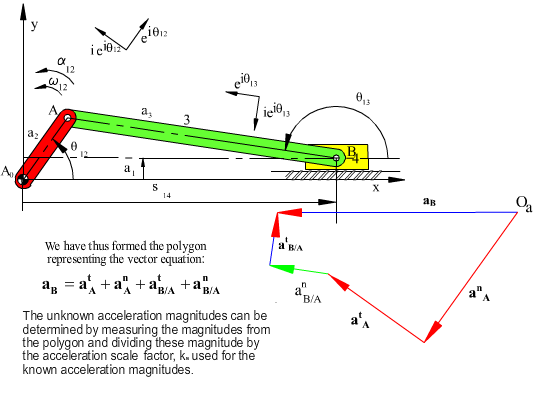
a_B = a_A + a^t_B/A + aⁿ_B/A

a_C = a_B + a^t_C/B + aⁿ_C/B

veya

a_D4 = a_D3 + a^t_D4/D3 + a^c_D4/D3

etc for acceleration. The points that one has to use are usually the revolute joint axes between the links since these are the points where the relative velocity or acceleration between the two coincident points on two different links are zero and they have equal velocity and accelerations. If we are to determine the velocity of a point on a link we must first determine the velocity of the points located at the joint axes.

Another important consideration is that the acceleration analysis cannot be performed without performing the velocity analysis since the normal and Coriolis acceleration components can only be determined after the velocity analysis.

Loop equations can be used very effectively for velocity and acceleration analysis since the loop equations contain the necessary position variables. When the loop equations are differentiated with respect to time we obtain “velocity loop equations”. If the position variables are solved beforehand, these velocity loop equations will always yield a linear set of equations in terms of velocity variables which are the time rate of change of the position variables of the mechanism. When these velocity variables are solved for a given input condition, the velocity of any point on any link can be determined.

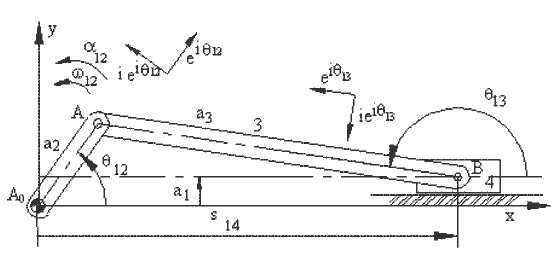
As a first example, consider a slider-crank mechanism shown above. We shall assume that θ₁₂ and its derivatives are known: $\displaystyle \text{ω}_{12}=\dot{θ}_{12}=\frac{{\text{d}{{\text{θ}}_{{12}}}}}{\text{dt}}$ , $\displaystyle {{\text{α}}_{{12}}}={{{\ddot{θ}}}_{{12}}}=\frac{{{{\text{d}}^{2}}{{\text{θ}}_{{12}}}}}{{\text{d}{{\text{t}}^{2}}}}$ . The loop closure and its complex conjugate is:

s₁₄ + ic₁ + a₃e^iθ₁₃ = a₂e^iθ₁₂

s₁₄ − ic₁ + a₃e⁻^iθ₁₃ = a₂e⁻^iθ₁₂

(1a)

(1b)

For a given value of θ₁₂ we have seen how the position variable s₁₄ and θ₁₃ can be solved. Differentiating the loop closure equation with respect to time we obtain the velocity loop equations as:

$\displaystyle {\dot{\text{s}}}$ ₁₄ + ia₃ω₁₃e^iθ₁₃ = ia₂ω₁₂e^iθ₁₂

$\displaystyle {\dot{\text{s}}}$ ₁₄ − ia₃ω₁₃e⁻^iθ₁₃ = −ia₂ω₁₂e⁻^iθ₁₂

(2a)

(2b)

where ω₁₂ = dθ₁₂/dt, ω₁₃ = dθ₁₃/dt, $\displaystyle {\dot{\text{s}}}$ ₁₄ = ds₁₄/dt are the velocity variables. Note that the velocity loop equation is nothing but the vector equation:

v_B + v_A/B = v_A

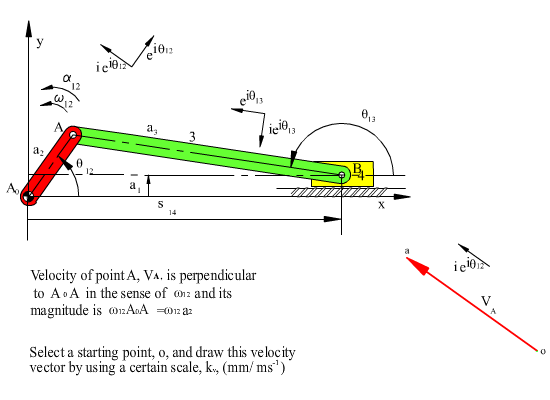
Physical explanation of the above equation is that point A is a permanently coincident point between links 2 and 3, since they are points on the revolute joint axis between these two links. Therefore v_A2 = v_A3 = v_A. If we consider link 2, it is in a fixed axis of rotation and point A on link 2 has a velocity perpendicular to AA₀ in the sense of ω₁₂ and its magnitude is |AA₀|ω₁₂. If we consider link 3, it is in a general plane motion. Points A and B are on this link. If we write the velocity of point A on link 3 using point B it is: v_A3 = v_B + v_A/B = v_A. v_A/B is perpendicular to AB. Point B is a permanently coincident point between links 3 and 4. Therefore v_B3 = v_B4 = v_B. If we consider link 4, it is in a translation. Therefore the velocity of every point is tangent to the path, which is the slider axis. In the velocity vector equation the unknowns are the magnitudes of v_B and v_A/B (which correspond to $\displaystyle {\dot{\text{s}}}$ ₁₄ and a₃ω₁₃ in the velocity loop equation).

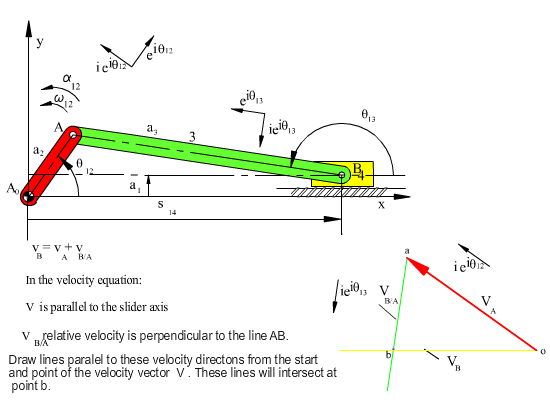
If the loop equations are to be solved graphically, unlike the analytical method where we group the unknowns on one side of the equality and the known values on the other side, we leave one unknown on both sides of the equation. The loop equation is rewritten as:

$\displaystyle {\dot{\text{s}}}$ ₁₄ = ia₂ω₁₂e^iθ₁₂ − ia₃ω₁₃e^iθ₁₃

which is the vector equation:

v_B = v_A + v_A/B

Note that

v_B/A = −v_A/B = −ia₃ω₁₃e^iθ₁₃

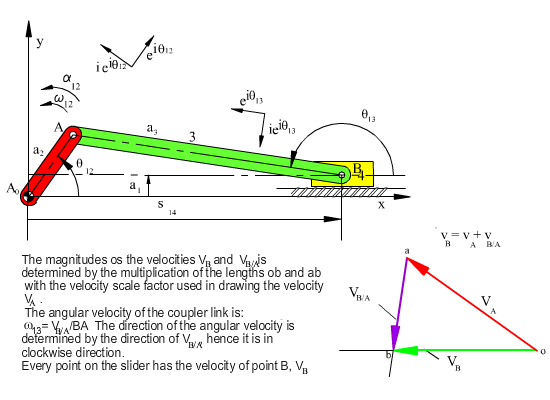
In order to determine the unknowns graphically, we first determine the magnitude of |v_A|= |AA₀|ω₁₂. Then using a certain scale factor, k_v, a directed line (vector) whose magnitude is proportional to v_A and direction of v_A is drawn (see figure below). From the starting point of this line, a line whose direction is that of v_B, and from the tip a line whose direction is that of v_B/Ais drawn (v_B is along the slider axis and v_B/A is perpendicular to AB). The point of intersection gives us the tips of the vectors representing the velocities v_B and v_B/A. If we measure these lengths and then divide by the scale factor we have used for v_A, the unknown magnitudes will be solved. The diagram thus obtained is known as the velocity polygon. For example if ω₁₃ = dθ₁₃/dt is to be determined, first the length of the vector v_B/A measured on the velocity polygon is divided by k_v to determine the actual value of v_B/A. Since v_B/A = a₃ω₁₃ and a₃ = |AB|, then ω₁₃ = v_B/A/a₃. The direction of the angular velocity of link 3 is determined by the direction of v_B/A. In the figure, since the velocity of point B relative to A (v_B/A) is downwards, in order to have this velocity at this position link 3 must have a clockwise angular velocity.

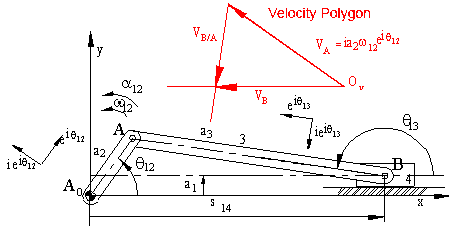
If the dependant position variables (s₁₄ and θ₁₃) are to be solved analytically for a corresponding input position θ₁₂, the velocity loop equation will always give a linear relation between the velocity variables (ω₁₂, ω₁₃ and $\displaystyle {\dot{\text{s}}}$ ₁₄). If the rate of change of the input variable (ω₁₂) is given, one can solve for the other two velocity variables ω₁₃) and $\displaystyle {\dot{\text{s}}}$ ₁₄ from the velocity equations by the methods of linear algebra. Since we have two equations (equations 2a and 2b) in two unknowns, we can apply Cramer’s rule:

$\displaystyle {{{\dot{\text{s}}}}_{{14}}}=\frac{{\left| {\begin{array}{cc} {\text{i}{{\text{a}}_{2}}{{\text{ω}}_{{12}}}{{\text{e}}^{{\text{i}{{\text{θ}}_{{12}}}}}}} & {\text{i}{{\text{a}}_{3}}{{\text{e}}^{{\text{i}{{\text{θ}}_{{13}}}}}}} \\ {-\text{i}{{\text{a}}_{2}}{{\text{ω}}_{{12}}}{{\text{e}}^{{-\text{i}{{\text{θ}}_{{12}}}}}}} & {-\text{i}{{\text{a}}_{3}}{{\text{e}}^{{-\text{i}{{\text{θ}}_{{13}}}}}}} \end{array}} \right|}}{{\left| {\begin{array}{cc} 1 & {\text{i}{{\text{a}}_{3}}{{\text{e}}^{{\text{i}{{\text{θ}}_{{13}}}}}}} \\ 1 & {-\text{i}{{\text{a}}_{3}}{{\text{e}}^{{-\text{i}{{\text{θ}}_{{13}}}}}}} \end{array}} \right|}}=\frac{{{{\text{a}}_{2}}{{\text{a}}_{3}}\left( {{{\text{e}}^{{\text{i}\left( {{{\text{θ}}_{{12}}}-{{\text{θ}}_{{13}}}} \right)}}}-{{\text{e}}^{{-\text{i}\left( {{{\text{θ}}_{{12}}}-{{\text{θ}}_{{13}}}} \right)}}}} \right)}}{{-\text{i}{{\text{a}}_{3}}\left( {{{\text{e}}^{{\text{i}{{\text{θ}}_{{13}}}}}}+{{\text{e}}^{{-\text{i}{{\text{θ}}_{{13}}}}}}} \right)}}{{\text{ω}}_{{12}}}$

\displaystyle {{{\dot{\text{s}}}}_{{14}}}=-{{\text{a}}_{2}}\frac{{\sin \left( {{{\text{θ}}_{{12}}}-{{\text{θ}}_{{13}}}} \right)}}{{\cos {{\text{θ}}_{{13}}}}}{{\text{ω}}_{{12}}}

(4)

and

\displaystyle {{\text{ω}}_{{13}}}=\frac{{\left| {\begin{array}{cc} 1 & {\text{i}{{\text{a}}_{2}}{{\text{ω}}_{{12}}}{{\text{e}}^{{\text{i}{{\text{θ}}_{{12}}}}}}} \\ 1 & {-\text{i}{{\text{a}}_{2}}{{\text{ω}}_{{12}}}{{\text{e}}^{{-\text{i}{{\text{θ}}_{{12}}}}}}} \end{array}} \right|}}{{\left| {\begin{array}{cc} 1 & {\text{i}{{\text{a}}_{3}}{{\text{e}}^{{\text{i}{{\text{θ}}_{{13}}}}}}} \\ 1 & {-\text{i}{{\text{a}}_{3}}{{\text{e}}^{{-\text{i}{{\text{θ}}_{{13}}}}}}} \end{array}} \right|}}=\frac{{-\text{i}{{\text{a}}_{2}}\left( {{{\text{e}}^{{\text{i}{{\text{θ}}_{{12}}}}}}+{{\text{e}}^{{-\text{i}{{\text{θ}}_{{12}}}}}}} \right)}}{{-\text{i}{{\text{a}}_{3}}\left( {{{\text{e}}^{{\text{i}{{\text{θ}}_{{13}}}}}}+{{\text{e}}^{{-\text{i}{{\text{θ}}_{{13}}}}}}} \right)}}{{\text{ω}}_{{12}}}=\frac{{{{\text{a}}_{2}}}}{{{{\text{a}}_{3}}}}\frac{{\cos {{\text{θ}}_{{12}}}}}{{\cos {{\text{θ}}_{{13}}}}}{{\text{ω}}_{{12}}}

(5)

Note that one can as well obtain two scalar equations by equating the real and imaginary parts of the velocity loop equation and solve for the velocity variables as well. For the slider-crank mechanism these two scalar equations will be:

$\displaystyle {\dot{\text{s}}}$ ₁₄ − a₃ω₁₃sinθ₁₃ = −a₂ω₁₂sinθ₁₂

(6)

and

a₃ω₁₃cosθ₁₃ = a₂ω₁₂cosθ₁₂

(7)

One will obtain exactly the same result from the solution of these two equations for the velocity variables ω₁₃ and $\displaystyle {\dot{\text{s}}}$ ₁₄.

For the acceleration analysis the velocity loop equations can be differentiated with respect to time to yield acceleration loop equations in terms of acceleration variables which are the second rate of change of the position variables. For the slider crank mechanism given, differentiating equations 2a and 2b with respect to time:

$\displaystyle {\ddot{\text{s}}}$ ₁₄ + ia₃α₁₃e^iθ₁₃ − a₃ω₁₃²e^iθ₁₃ = ia₂α₁₂e^iθ₁₂ − a₂ω₁₂²e^iθ₁₂

$\displaystyle {\ddot{\text{s}}}$ ₁₄ − ia₃α₁₃e^-iθ₁₃ − a₃ω₁₃²e^-iθ₁₃ = −ia₂α₁₂e^-iθ₁₂ − a₂ω₁₂²e^-iθ₁₂

(8a)

(8b)

where α₁₂ = d²θ₁₂/dt², α₁₃ = d²θ₁₃/dt², $\displaystyle {\ddot{\text{\text{s}}}}$ ₁₄ = d²s₁₄/dt²are the acceleration variables.. Note that this equation can be written as a vector equation in the form:

a_B + a^t_A/B + aⁿ_A/B = a^t_A + aⁿ_A

The acceleration loop equations are linear in terms of the acceleration variables (α₁₂, α₁₃ and $\displaystyle {\ddot{\text{s}}}$ ₁₄). If the input angular acceleration, α₁₂ is known, these two equations can be solved for the unknowns α₁₃ and $\displaystyle {\ddot{\text{s}}}$ ₁₄ using Cramer’s rule :

\displaystyle {{\text{α}}_{{13}}}=\frac{{{{\text{a}}_{2}}{{\text{α}}_{{12}}}\cos {{\text{θ}}_{{12}}}-{{\text{a}}_{2}}{{\text{ω}}_{{12}}}^{2}\sin {{\text{θ}}_{{12}}}+{{\text{a}}_{3}}{{\text{ω}}_{{13}}}^{2}\sin {{\text{θ}}_{{13}}}}}{{{{\text{a}}_{3}}\cos {{\text{θ}}_{{13}}}}}

(9)

$\displaystyle {\ddot{\text{s}}}$ ₁₄ = −a₂α₁₂sinθ₁₂ − a₂ω₁₂²cosθ₁₂ + ia₃α₁₃sinθ₁₃ + a₃ω₁₃²cosθ₁₃

(10)

Another approach is to differentiate the equations 4 and 5 directly to obtain acceleration variables. For example, differentiating equation 5, angular acceleration of link 3 will be obtained in the form:

$\displaystyle {{\text{α}}_{{13}}}=\frac{{{{\text{a}}_{2}}}}{{{{\text{a}}_{3}}}}\frac{1}{{{{{\cos }}^{2}}{{\text{θ}}_{{13}}}}}\left[ {\cos {{\text{θ}}_{{12}}}\cos {{\text{θ}}_{{13}}}{{\text{α}}_{{12}}}-\sin {{\text{θ}}_{{12}}}\cos {{\text{θ}}_{{13}}}{{\text{ω}}_{{12}}}^{2}+\cos {{\text{θ}}_{{12}}}\sin {{\text{θ}}_{{13}}}{{\text{ω}}_{{12}}}{{\text{ω}}_{{13}}}} \right]$

Although the terms may look different one will obtain the same result in either case.

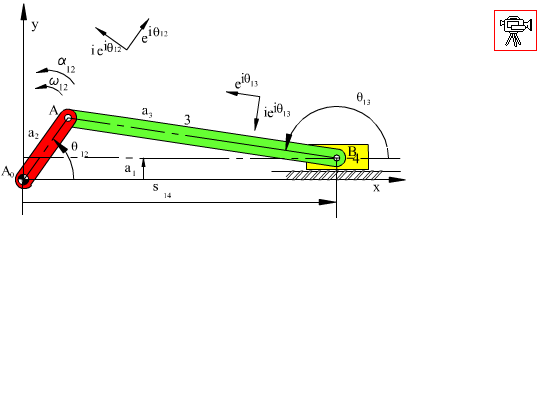
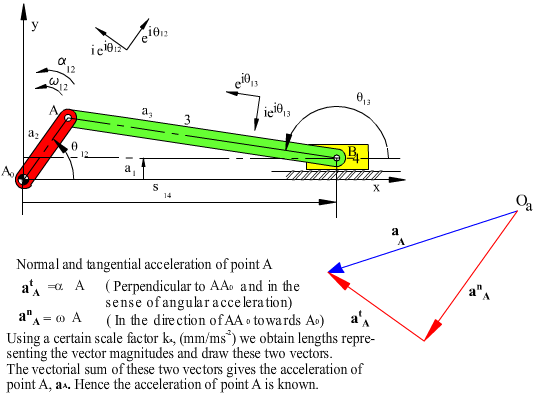
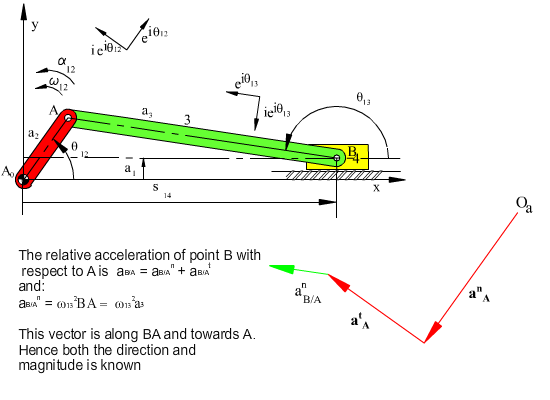
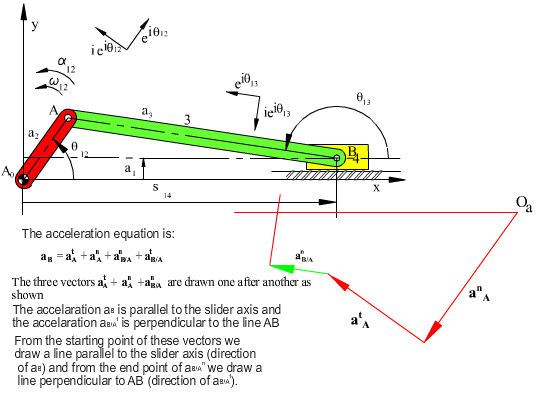
Graphically, the acceleration loop equation can be solved by rewriting the acceleration vector loop equation as:

a_B = a^t_A + aⁿ_A + a^t_B/A + aⁿ_B/A

where a_B/A = −a_A/B . The reason why the equation is written in this form is that we want to leave one unknown on each side of the equality. The magnitude of a_B is one unknown and the magnitude of a^t_B/A is the other unknown. Since the input angular velocity and acceleration are given a^t_B/A and aⁿ_B/A are known. If the velocity analysis is performed, magnitude of aⁿ_B/A will be determined. We utilise a scale factor k_a, to convert the acceleration vector magnitudes to a certain length. Starting with the vector a^t_A or aⁿ_A we draw the vectors a^t_A, aⁿ_B/A and aⁿ_B/A of known magnitude and direction in an end-to-tip form as shown below. Then we draw a line in the direction of a^t_B/A, which must be perpendicular to the line AB. The acceleration vector a_B must be parallel to the slider axis. From the starting point we then draw a line parallel to the slider axis. The intersection of the two lines drawn will determine the magnitudes of a_B and a^t_B/A. The diagram thus obtained is known as the acceleration polygon. When we divide the measured magnitudes with the scale factor k_a, we will obtain acceleration magnitudes.

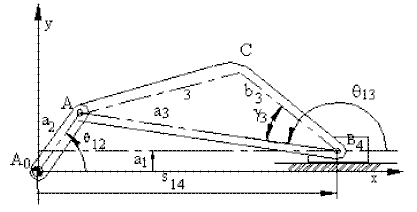
After obtaining the velocity and acceleration variables, one can determine the velocity and acceleration of any point C on the coupler link by writing its position vector in terms of position variables and differentiate the position vector to obtain the velocity and acceleration of point C. Referring to the figure above, The position vector r_C is:

r_C = s₁₄ + ic₁ + b₃e^{i(θ₁₃−γ₃)}

(11)

Velocity and acceleration of point C is:

v_C = $\displaystyle {\dot{\text{s}}}$ ₁₄ + ib₃ω₁₃e^{i(θ₁₃−γ₃)}

a_C = $\displaystyle {\ddot{\text{s}}}$ ₁₄ + ib₃α₁₃e^{i(θ₁₃−γ₃)} − b₃ω₁₃²e^{i(θ₁₃−γ₃)}

(12)

(13)

These equations are nothing but the vector equations:

v_C = v_B + v_C/B
and
a_C = a_B + a^t_C/B + aⁿ_C/B

If one has solved the position (θ₁₃ and s₁₄), velocity (ω₁₃ and $\displaystyle {\dot{\text{s}}}$ ₁₄) and acceleration parameters (α₁₃ and $\displaystyle {\dot{\text{s}}}$ ₁₄) for the given input condition (θ₁₂, ω₁₂ and α₁₂), then note that all of the terms on the right hand side are known and one can determine the position, velocity and acceleration of point C.

For the graphical solution, we can draw the vector equations for the velocity and acceleration of point C directly on the velocity and acceleration polygons drawn for the loop equations. Note that the velocity and acceleration of point C cannot be determined before solving the velocity and acceleration loop equations. From the tip of the vector v_B, if we draw the velocity vector v_C/B, the vector joining the starting point of v_B to the tip of the vector v_C/B will give us the velocity of point C. Similarly, the acceleration of point C can be determined by drawing the acceleration vectors aⁿ_C/B and a^t_C/B starting from the tip of the vector a_B. The acceleration vector from the starting point of a_B to the tip of the vector a^t_C/B, will give us the acceleration of point C. Alternatively, note that the position of point C could have been written as:

r_C = a₂e^iθ₁₂ + c₃e^{i(θ₁₃ + β₃ − π)} = a₂e^iθ₁₂ − c₃e^{i(θ₁₃+β₃)}

by differentiation:

v_C = ia₂ω₁₂e^iθ₁₂ − ic₃ω₁₃e^{i(θ₁₃+β₃)}

a_C = ia₂α₁₂e^iθ₁₂ − a₂ω₁₂²e^iθ₁₂ − ic₃α₁₃e^{i(θ₁₃+β₃)} + c₃ω₁₃²e^{i(θ₁₃+β₃)}

which are velocity and acceleration vector equations:

v_C = v_A + v_C/A
and
a_C = aⁿ_A + a^t_A + a^t_C/A + aⁿ_C/A

Let us label the tips of the vectors of the velocity and acceleration polygon by a lower case letter corresponding to the point whose velocity is represented (in case of acceleration the acceleration of point A and C are the sum of two or more acceleration vectors). The tips of the velocity vector v_A, v_B, v_C and a_A, a_B, a_C form triangles abc. We have an important theorem known as Mehmke’s Theorem or “The principle of the velocity and acceleration image” :

The triangles abc formed on the velocity and acceleration polygons are similar to the triangle ABC of the mechanism link. The sense of abc is similar to the sense of ABC (if there is a counter-clockwise rotation when going from A to B to C, there must be a counter clockwise rotation when moving from a to b to c on the velocity and acceleration polygons).