Number of Independent Loops in a Mechanism

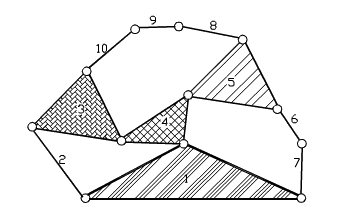
We can determine the number of independent loops in a mechanism from the number of joints and links in a mechanism. Consider a mechanism of l links and j joints and disconnect as many joints as required so that there are no loops in the mechanism.

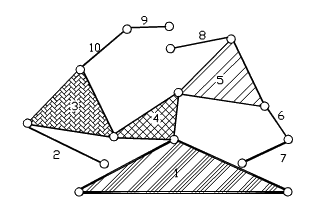
For example, in the ten-link mechanism shown in Fig. 2.17(a), we can disconnect the joints between links 1-2, 8-9 and 1-7 (the joints that are disconnected are not unique, but the number of joints that one must disconnect so that there are no loops left is unique). The open kinematic chain thus obtained is shown in Fig. 2.17.(b). As it can be seen from this example the number of joints that have been disconnected is equal to the number of loops in the mechanism. Furthermore, for the remaining open kinematic chain, the number of links is still  l and the number of joints is one less than the number of links (l-1). If L is the number of independent loops, we then have:

j = the number of joints in the open kinematic chain + the number of joints removed.

j = (l − 1) + L

or

L = j – l + 1

This simple equation (which is known by Euler’s polyhedron formula) can tell us the number of independent loops in a mechanism. However, it cannot tell us which loop equations are dependent on the other. Furthermore, since we can write a vector equation for each loop, the number of dependent motion parameters will be 2L. For a constrained motion, the number of independent motion parameters will be equal to the degree-of-freedom of the mechanism, F. Hence, there will be 2L+F variable parameters in the loop equations.

Note:

1. The number of loops in a mechanism does not depend on the type of joints.

2. The number of loops does not depend on the degree of freedom of space

3. The number of loops does not depend on the degree of freedom of the mechanism

Example:

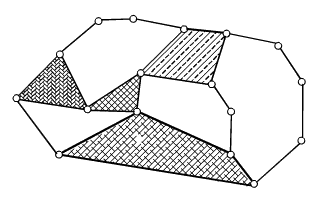
Determine the number of independent loops for the kinematic chain shown.

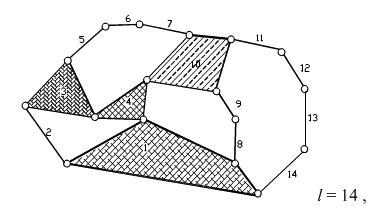
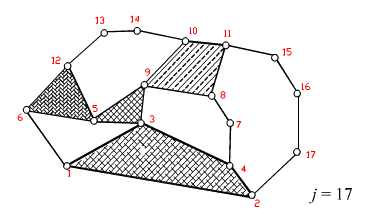
Hence L = 17 − 14 + 1 = 4
There are 4 independent loops.

Example:

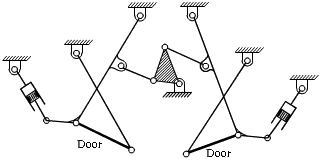
Determine the number of loops for the automatic door opening mechanism.

Since l = 15 and j = 19; L = 20 − 14 + 1 = 5 . There are 5 independent loops.