2.5 Enumeration of Kinematic Chains and Mechanisms

The dictionary meaning of enumeration is “to list one by one; to count”. Kinematic enumeration is the process of determining all possible kinematic chains or mechanisms satisfying certain predetermined criteria. There are elegant mathematical methods for the enumeration of kinematic chains (such as graph theory). Here we shall discuss cases that we can enumerate by sight.

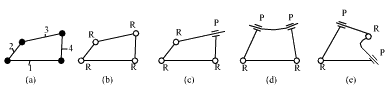
Consider kinematic chains that satisfy Grübler’s equation. If the number of links is restricted to four, than the number of joints is four and all the links are binary. Without considering the type of joint (revolute or prismatic) we have one type of kinematic chain (Figure a). If we also consider the type of joint in our enumeration, we can have four different kinematic chains (Figures b, c, d, e). Note that we cannot possibly have three or four prismatic joints (why?). Once the kinematic chain is obtained, using kinematic inversion, one can then enumerate for all possible mechanisms.

The next highest link number that satisfies Grübler’s equation is l= 6, and the number of joints must be 7. Using the conclusions that were derived, we can at most have links with 3 kinematic elements (ternary links) and we must also have 4 binary links. The only possible combination is 4 binary and 2 ternary links. (since 2j = 2l₂ + 3 l₃ and l₂= 4, l₃ = 2 for j = 7 is the only possible integer solution to the equation). These links may be combined in two different forms, thus yielding two different types of kinematic chains without considering the type of joint (Figure below).In the Watt’s Chain the two ternary links are connected to each other, whereas in Steffenson’s chain the two ternary links are not directly joined. (Historically, these two men are the ones who started the industrial revolution by designing the steam engine.)

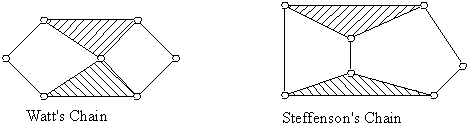
If the distance between the two kinematic elements on a ternary link goes to zero, we have limitting cases of Watt and Steffenson chains. The joint degree will increase and the two limitting chains we be as shown below. These are the special cases of 6 link chains.

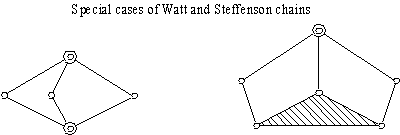
One can then obtain different kinematic chains (different in terms of the type of joint) by using sliding joints instead of revolute joints. One must keep in mind the restrictions concerning the kinematic chains formed by sliding and turning joints only.

As a simple example, consider a six-link mechanism driven by a piston cylinder. Let the cylinder be connected to the fixed link by a revolute joint. All other joints, except the piston cylinder are revolute joints.

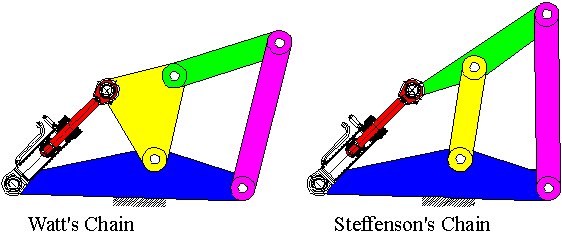
A piston-cylinder can be considered as two binary links connected by a prismatic joint. Hence in Watt’s chain or in Streffenson’s chain a piston-cylinder must replace the two binary links connected to each other. In Steffenson’s chain there is a unique location where the piston-cylinder can be placed. In case of Watt’s chain although there two different locations, due to symmetry of the chain, there is no difference. Since the cylinder must be connected to the fixed link, there are two different six link mechanisms that satisfy these conditions. The result is as shown above

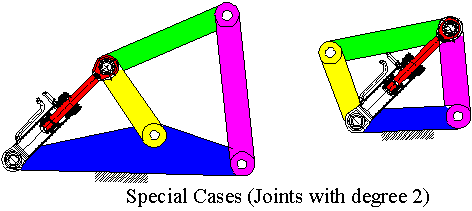
The special 6 link chains can also be used. There are two special chains where one or two link dimension of a ternary link is zero. In practice, the truck dump mechanism, cement pump boom, loaders and back-hoe systems all use the above chains. Two practical examples, log grabber and back-hoe, are shown below.