2.1 Degree of Freedom of Mechanisms-2

In the previous examples, we have seen that the degree of freedom does not depend on the link lengths or the free parameter used. We must be able to determine an equation that relates the degree of freedom of a mechanism with the number of links, number of joints and the degree of freedom of the joints. To express these quantities in mathematical terms let us define:

λ : Degree of freedom of space

(λ = 3 for planar space ;  λ = 6 for general (spatial) space)

l : The number of links in a mechanism (including the fixed link)

j : The number of joints in a mechanism

f_i : The degree of freedom of the i th joint in the mechanism

F : The degree of freedom of the mechanism

First consider l links floating freely (no joints!!) in a space with λ freedom. In such a case, apart from the fixed link (the fixed reference frame is attached to this link. Therefore no parameter is required to determine the position of this link), we will need λ parameters for each link. Since there are l − 1 floating links, when there are no joints in the mechanism, the number of parameters required to determine the position of every link is:

λ(l − 1)

(1)

 

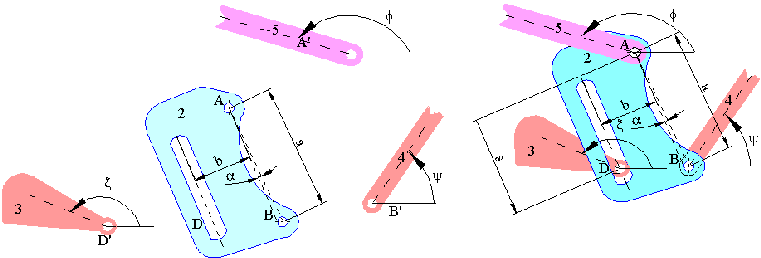
Now, consider the joints by utilizing a simple example. In the above figure there are four floating links in planar space. If there are no joints, then the number of parameters requires to determine the position of these links will be 3 × 4 = 12. If link 2 is connected to links 4 and 5 by revolute joints, and if there is a cylinder in slot joint between links 2 and 3, the number of parameters required to determine the position of these four links will be less. We will still need 3 parameters to determine the position of link 2. Once the position of link 2 is known, links 4 and 5 can only rotate relative to link 2, and link 3 can rotate and translate along the slot axis relative to link 2. To locate the position of link 4 we need ψ angle (1 new parameter), to locate the posion of link 5 we need ϕ (1 new parameter) and to locate the position of link 3 we need 2 new parameters (s and ζ). Thus the total number of parameters required is 3 + 1 + 1 + 2 = 7 instead of 12, when there were no joints. In planar space we need 2 less parameters for the revolute joint and one less parameter for the cylinder in slot joint. This means, we don’t need to define a parameter in the direction for which the motion is constrained.

If the degree-of-freedom of space is λ, a kinematic joint with f_i degrees-of-freedoms constrains (λ − f_i) degrees-of-freedom and we need not define this many number of parameters. Since there are different joints with different degrees of freedom, in a mechanism with j joints, the total number of freedoms constrained by all the joints will be:

\displaystyle {\sum\limits_{{\text{i}=1}}^{\text{j}}{{\left( {\lambda -{\text{f}_\text{i}}} \right)}}=\text{λ} \text{j}-\sum\limits_{{\text{i}=1}}^{\text{j}}{{{{\text{f}}_{\text{i}}}}}}

(2)

The degree of freedom of the mechanism will then be the degrees-of- freedom of all the links without joints minus the degrees of freedom constrained by the joints.

F = Degrees of freedom without any joint (1) – constraints imposed by the joints (2)

\displaystyle {\text{F}=\text{λ} \left( {l-1} \right)-\left( {\text{λ}\text{j}-\sum\limits_{{\text{i}=1}}^{\text{j}}{{{{\text{f}}_{\text{i}}}}}} \right)}

or

\displaystyle {\text{F}=\text{λ} \left( {l-\text{j}-1} \right)+\sum\limits_{{\text{i}=1}}^{\text{j}}{{{{\text{f}}_{\text{i}}}}}}

This equation is known as the “General Degree-of-Freedom Equation”.

Although this equation is applicable to most of the mechanisms, there are exceptions, i.e. the degree-of-freedom of the mechanism may not obey the general degree-of-freedom equation. This is mainly due to the assumption that the constraints imposed by the joints are independent of each other, and the degree-of-freedom of the space is constant for the whole mechanism. Before discussing these exceptions let us see some mechanisms that obey the general degree-of-freedom equation.