1.3 Basic Concepts-3

Link-Kinematic Chain

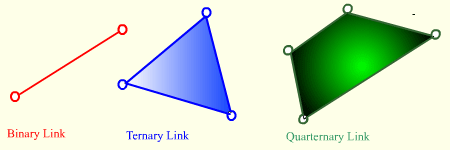
If a rigid body contains at least two kinematic elements we shall call it a link. A link may have more than two kinematic elements (but not less than two). One can classify links according to the number of kinematic elements it contains. These are binary, ternary or quarternary, etc.

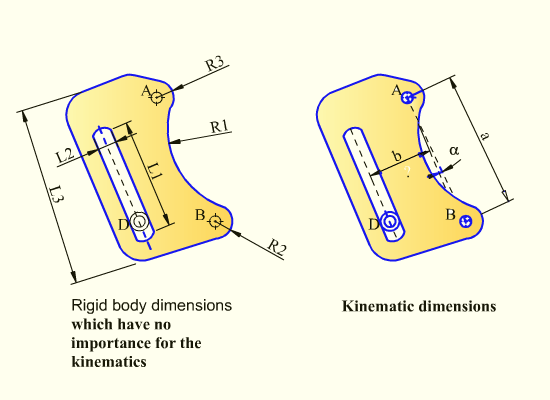
The kinematic dimensions of a link in a mechanism are those dimensions which define the relative positions of the kinematic elements on that link and when these dimensions are specified, the link dimensions are known for motion analysis. These dimensions can be distances or angles. For the manufacture of the link or for the dynamics, etc other physical dimensions such as the width, height, thickness, etc. may be important. For the kinematic analysis we shall be interested only with the kinematic dimensions. As seen with the above figure, on the link at points A and B kinematic elements form revolute joins, whereas at D there is a cylinder in slot joint. For manufacture besides the thickness, one must specify the radii ( R₁, R₂, R₃), the slot length and width (L₁, L₂), the length of the piece (L₃) etc. These have no importance for kinematics. Whereas the distance between revolute joints A and B (a), the angle slot makes with respect to the line AB (α) and perpendicular distance from point A to the slot axis (b)are the kinematic dimensions of this link. Once these four parameters are known, the link is kinematically defined.

The links connected to each other by kinematic pairs will form a kinematic chain. If all the kinematic pairs are closed, than we have a closed kinematic chain. If one of the kinematic pair is of open type, the kinematic chain is an open kinematic chain.

Kinematic chain is an idealised representation of the mechanism structure. We are not concerned with the dimensions of the links. Each link is represented as a line or as a polygon and at each vertex we have a kinematic element which joins with another element on another link. The dimensions of the edges are not important.

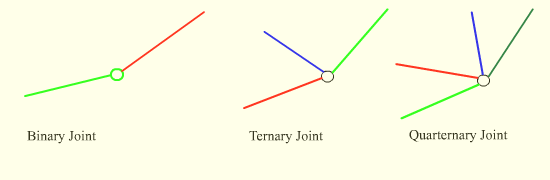
There are certain joints where more than two links are connected. For such cases we define the degree-of a joint as the number of links connected at the joint minus one. One must assume that there joints at this point equal to the degree of the joint, (please do not confuse the degree of the joint with the degree-of-freedom of a joint)

If all the links forming a kinematic chain are in the same plane or in parallel planes, the kinematic chain formed is said to be “Planar kinematic chain “. If all the points on all the links move on concentric spheres than the kinematic chain formed is “Spherical kinematic chain “. If some of the links have a general spatial motion than we have “Spatial kinematic chain” .

If one of the links in a kinematic chain is fixed, then the system thus obtained is called a mechanism. Although we have worded the definition of a mechanism differently before, there is no contradiction between the definitions. In fact, they are more or less identical.