1.3 Basic Concepts-2
Degree of Freedom
Some of the classifications used in the previous page are important in terms of force transmission (i.e. lower or higher kinematic pairs) or in terms of physical construction (i.e. form or force closed kinematic pairs). However the most important characteristics of the kinematic pairs is type of motion that may exist between the kinematic elements. Depending on the type of kinematic pair used, there will exist different motion characteristics between the mating parts. Since there are two rigid bodies connected by a kinematic pair, they will have different relative motions with respect to each other according to the type of the kinematic pair.The type of relative motion is the basic charactyeristics of that kinematic pair. In order to classifiy this relative motion we have to understand the degree of freedom concept.
The degree-freedom of space is the number of independent parameters to define the position of a rigid body in that space.
Let us define the position of a rigid body in a three dimensions space (in which we live). The first thing we must do is define a refernce axis such as X,Y,Z in the figure. One form of defining the position of the rigid body is that we may arbitrarily select any three noncollinear points, (P1, P2, P3) and determine their location with respect to the ref-erence plane (see figure on the right). Once the location of these points are known with respect to the reference axis, the location of any other point can be determined since the distance of the particular point we are considering from P1, P2 and P3 is constant (rigid body). For each one of the three points we have to define three parameters (P1(x1, y1, z1), P2 (x2, y2, z2) ve P3 (x3, y3, z3)), However, due to the rigid body concept we also have the following three equations relating these parameters:
(x2 − x1)2 + (y2 − y1)2 + (z2 − z1)2 = a12
(x3 − x1)2 + (y3 − y1)2 + (z3 − z1)2 = a22
(x3 − x2)2 + (y3 − y2)2 + (z3 − z2)2 = a32
We have nine parameters (xi, yi, zi : i =1,2,3) and three relations among them. Therefore, if we define any six of these nine parameters, the location of the rigid body is known. Therefore In the general space the degree of freedom is six.
Question : Are the parameters required unique?
We can also use angles to locate the rigid body: In this case, we may take a point A and a line passing through this point A. From the rigid body concept, if we know the position of A and the orientation of the line, the position of the rigid body is determined. In this case we have seven parameters (xa, ya, za, θ1, θ2, θ3 and ϕ). We also have a relation between θi in the form:
cos2(θ1) + cos2(θ2) + cos2(θ3) = 1
Hence, by defining six parameters (xa, ya, za, ϕ and any two of the parameters θ1, θ2, θ3) , we can locate the rigid body completely.
Degree of freedom of Planar Spac:
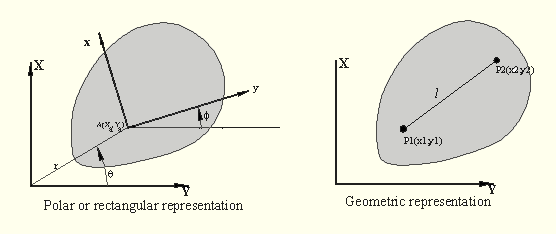
If the space that we consider is a plane, then we only need 3 parameters. Different forms of selecting these three parameters are shown below. ( polar, rectangular and geometrical representations) .Hence, for spatial motion the degree-of freedom of space is 6 and for planar motion the degree-of-freedom of space is 3. There are some other spaces (ie. spherical space) which we shall discuss later. The spatial and planar spaces are the two most common spaces.
The degree-of-freedom of a kinematic pair is defined as the number of independent parameters that is required to determine the relative position of one rigid body with respect to the other connected by the kinematic pair. It is this characteristics that is used to classify the kinematic pairs. If the degree-of-freedom of a kinematic pair is 6, there is no joint involved. If the degree-of-freedom is 5, the kinematic pair must constrain one of the freedoms of space. There is no joint that can constrain the rotational degree-of-freedom while permitting the transla-tional freedom in all directions. We can constrain one of the translational freedoms. The joint thus obtained is sphere between parallel planes. Methodically, all the possible kinematic pairs are shown in Table I and Table II. Note that the shapes of the kinematic pairs shown is of no importance. It is the degree-of-freedom and the type of freedom that is important. Please study these tables carefully so that you can identify kinematic pairs that you will see in mechanisms study and in your practical life.
What is important for the joints is the type of motion permitted between the rigid bodies connected by the joints. The shape, size and the material used has no significance in identifying the joints (Please study Table I and Table II).
