3.9 Devre Kapalılık Denklemlerinin İteratif Yöntemle Çözülmesi

Önceki kısımlarda devre kapalılık denklemleri kullanılarak konum değişkenleri arasında analitik ilişkiler değişik yöntemlerle bulunmaya çalışılmıştır. Genel olarak her bir devre kapalılık denkleminde iki yeni bilinmeyen konum değişkeni bulunuyor ise, bu iki bilinmeyen için analitik bir çözüm elde edilebilecektir. Bu durumlarda denklemleri bilinmeyen konum parametrelerine göre önceki kısımlarda gösterildiği gibi, doğrudan çözmek daha uygundur. Eğer devre kapalılık denklemlerinin her birinde ikiden fazla bilinmeyen konum değişkeni var ise, bu konum değişkenlerini bağımsız konum değişkenine göre belirlemek genel olarak mümkün değildir (bazı özel durumlarda mümkün olabilir). Bu durumlar geometrik yöntem uygulandığında deneme-yanılma gerektirmiştir. Ancak eğer mekanizma serbestlik derecesine uyuyor ise, elde edilen vektör devre denkleminin iki katı kadar bilinmeyen konum değişkeni ve serbestlik derecesi kadar bağımsız konum değişkeni bulunacaktır. Analitik çözüm elde edilemediği durumlarda veya her türlü mekanizmanın analizini yapmak için genel bir algoritma oluşturmak istediğimizde, devre kapalılık denklemlerinin sayısal yöntemlerle iteratif (yinelemeli) çözümü düşünülmelidir.

Devre kapalılık denklemlerine baktığımızda, her birinden iki lineer olmayan cebirsel denklem elde edeceğimize göre, bu denklemler:

Fj(x) = 0	j = 1, 2, 3, …, n	(1)
	x = [x1 x2 x3 … xn]T

şeklinde yazılabilir. Bu gösterimde F_k(x) devre kapalılık denkleminden elde edilen karmaşık sayılar veya reel sayılarla ifade edilebilen devre sayısının iki katı kadar lineer olmayan denklem takımıdır. Vektör x ise bilinmeyen konum değişkenleri: θ_1j veya s_ij den oluşur. F_j(x) ve türevleri, çözümü olduğu bölgede tanımlı ise, F_j(x) = 0 denklemlerinin bilinmeyen değerlere göre çözümü Newton-Raphson metodu olarak bilinen iterasyon metodu ile yapılabilir. Bu metod denklemleri küçük aralıklarda lineer olarak kabul eder ve bu lineer denklem takımı için çözüm bularak lineer olmayan denklem takımının çözüme doğru yaklaşıp yaklaşmadığını kontrol eder (F_j(x) = ε ise, her basamakta lineer denklem çözümünün ε değerini daha küçültüp küçültmediği) ε’un yeteri kadar küçük değerini veren x bilinmeyen değerleri çözümdür. Bu tür lineer olmayan denklem takımlarını çözmek için başka nümerik yöntemler de mevcuttur. Burada gerek basit olması ve gerekse mekanizmaların çözümünde oldukça iyi sonuç vermesi nedeni ile Newton-Raphson metodu açıklanacaktır. Okuyucu herhangi bir nümerik metod kitabından diğer yöntemleri öğrenebilir.

F(x) = 0 gibi tek değişkenli bir denklemi ele alalım. Denklem skaler değişken x’e göre lineer değildir. Bu denklemde x = x* değerinin denklemin çözümü (kökü) olduğunu (yani F(x*) = 0) ve x^(k) nın ise, x* değerine yakın bir değer olduğunu kabul edelim. F(x) denkleminin x = x^(k) noktası civarında Taylor serisi açılımını yaparsak

F(x) = F(x(k)) + Fx(x(k))(x − x(k)) + (yüksek mertebe terimler)

(2)

olur. F_x(x), F(x) denkleminin x’e göre birinci türevidir: F_x(x) = dF(x)/dx. Eğer x^(k) = x* olsa idi, F(x^(k)) = 0 olacak ve x^(k) aradığımız çözüm olacak idi. Hatalardan dolayı bu olmayacaktır.

x = x^(k+1) in x* çözüm değerine x^(k) dan daha yakın bir tahmin olduğunu varsayalım. F(x^(k+1)) ≈ 0 olduğu varsayılır ve F(x^(k+1)) için Taylor serisi kullanılarak x^(k) ya göre açılımı yazıldığında:

F(x(k+1)) ≈ F(x(k)) + Fx(x(k))(x(k+1) − x(k)) = 0

(3)

olacaktır. x^(k+1) − x^(k) aralığı yeterince küçük ise veya denklem lineer ise, yüksek mertebe terimlerin ihmal edilmesi büyük bir yanlışa neden olmayacaktır (tabi eğer sonsuz sayıda terim kullanıp seriyi sıfıra eşitleyip çözüm yapsak x*’ı hemen bulabilirdik. Ne yazık ki bu mümkün değil, ve sadece ilk terimle yetineceğiz). Eğer F_x(x^(k)) sıfıra eşit değil ise, (3) denkleminden x^(k+1) çözülebilir:

x(k+1) = x(k) − F(x(k))/Fx(x(k))

(4)

(4) denklemi Newton-Raphson metodu ile elde edilen tekrarlama denklemidir. Yüksek mertebe terimler ihmal edilmiş olduğundan, x^(k+1) denklemi sıfıra eşitleyen çözüm değildir. Ancak x^(k) ya göre x*’a daha yakın bir noktaya gelinebilecektir. Yeni değer ile denklemin sıfıra daha yaklaştığı görülür ise, (4) denklemini tekrar tekrar kullanmamız mümkün olacak ve m defa uygulandıktan sonra |F(x^(m))| < ε olacaktır. Burada ε, kendisinden küçük olan değerleri sıfır kabul edebileceğimiz küçük bir değerdir. Tabi ki ε probleme göre değişecek ve bazı problemlerde m sayısı ne kadar büyük olursa olsun |F(x^(m))| < ε şartı sağlanamayacaktır (yakınsama olmayacaktır). Birçok uygulama için örneğin ε = 10^-6 gibi küçük bir değer kabul edilebilir. Bu durumda F(x) = 0 denklemini sağlayan x değerini bulmak için bir algoritma ortaya çıkacaktır:

1. F(x) = 0 denklemini sağlayacak x* değeri için x⁽⁰⁾ değerini tahmin edelim.
2. F(x^(k+1)) değerini k = 0, 1, 2, …, m, basamak kadar (4) numaralı denklem kullanarak etap etap belirleyelim ve her etapta |F(x^(k+1))| < ε_e olup olmadığını veya |x^(k+1) − x^(k)| < ε_s olup olmadığını kontrol edelim. Bu iki eşitsizlikten birisi sağlanıyor ise duralım. x^(k+1) aradığımız çözümdür. (ε_e denklem hata toleransı, ve ε_s ise çözüm hata toleransıdır). Eğer F_x(x^(k+1)) = 0 ve F(x^(k+1)) ≠ 0 ise, 1. basamağa gidip yeni bir x⁽⁰⁾ tahmini yapılması gereklidir. Aksi takdirde işlem devam eder.
3. k+1 yerine k yerleştirip 2 basamak tekrarlanır. Eğer işlem m defa tekrarlandığı halde |F(x^(k+1))| < ε_e veya |x^(k+1) − x^(k)| < ε_s sağlanamamış ise, çözüm bulunamamıştır. Durulması gerekir. İşleme yeni bir x⁽⁰⁾ değeri ile yeniden başlanabilir veya farklı bir yöntem denenebilir.

Newton-Raphson algoritması çoğu uygulama probleminde gittikçe çözüme yaklaşan bir dizi sonuç verecektir. Genel olarak |F(x)| < ε_e şartına sınırlı sayıda basamakta erişilecektir. Ancak eğer x⁽⁰⁾ değeri x*’a yeteri kadar yakın değilse, ε_e ve ε_s değerleri eldeki probleme göre çok küçük seçildi ise, veya çözülmesi istenilen problemde F(x) fonksiyonu ve türevleri düzgün ve yumuşak bir davranış göstermiyorlarsa, çözüm bulunamayabilir. Bazı durumlarda ise, bulunan çözüm aranılan x* çözümü olmayabilir (lineer olmayan denklemlerde F(x) = 0 denklemini sağlayan birden fazla kök olabilir).

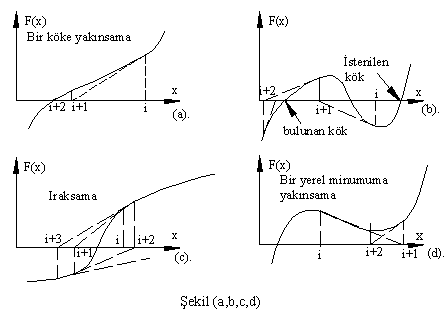
Geometrik olarak Newton-Raphson yöntemi aşağıda Şekil (a) da gösterilmektedir. Her noktada F(x) eğrisi, eğimi F_x olan bir doğru olduğu kabul edilmekte ve o doğrunun kökü (sıfır olan x değeri) bulunmaktadır. Normal durumlarda kök çok az sayıda basamakta hızla bulunabilir. Ancak Şekil (b),(c), ve (d) de görüldüğü gibi, yöntem bazı durumlarda istenilen çözüme yönelmeyebilir, veya hiçbir çözüm bulunamayabilir.

    

Şu ana kadar Newton-Raphson metodu bir değişkenli bir denklem için açıklanmıştır. Aynı yöntem kolaylıkla n bilinmeyenli n lineer olmayan denklem takımının çözümü için kullanılabilir. Bu durumda Newton-Raphson algoritmasını genelleştirmemiz gerekecektir. n bilinmeyenli n lineer olmayan denklem takımı:

F1(x) = F1(x1, x2, x3, …., xn) = 0 F2(x) = F2(x1, x2, x3, …, xn) = 0 F3(x) = F3(x1, x2, x3, …, xn) = 0 …… Fn(x) = Fn(x1, x2, x3, …, xn) = 0

(5)

veya:

F(x) = 0

olarak yazılabilir. Çözüm x* = [x*₁ x*₂ x*₃ … x*_n]^T dir. Denklemleri kök olduğunu tahmin ettiğimiz değer olan x^(k) = [x^(k)₁ x^(k)₂ x^(k)₃ … x^(k)_n]^T noktasında Taylor serisine göre açalım ve seride sadece birinci mertebe terimleri tutalım (diğer terimleri tek denklem için yaptığımız gibi, sıfıra çok yakın değerler olduğunu kabul edip ihmal edeceğiz). Bu durumda:

F(x) ≈ F(x(k)) + Fx(x(k))(x − x(k))

(6)

olacaktır. Bu denklemde F_x(x^(k)), x^(k) noktasında hesaplanan Jacobian matrisidir^#. Eğer x = x^(k+1) çözüme daha yakın bir değer olması isteniyor ise, x^(k) dan daha iyi bir değer:

F(x^(k+1)) ≈ F(x^(k)) + F_x(x^(k))(x^(k+1) − x^(k)) = 0

---

^# Jacobian matrisi: F_x = \displaystyle \left[ {\begin{array}{cccc} \text{F}_{1\text{x}_1}&\text{F}_{1\text{x}_2}&\cdots&\text{F}_{1\text{x}_\text{n}} \\ \text{F}_{2\text{x}_1}&\text{F}_{2\text{x}_2}&\cdots&\text{F}_{2\text{x}_\text{n}} \\ \vdots&\vdots&\ddots&\vdots \\ \text{F}_{\text{nx}_1}&\text{F}_{\text{nx}_2}&\cdots&\text{F}_{\text{nx}_\text{n}} \end{array}} \right]

burada F_kxm, F_k nın x_m e göre kısmi türevidir.

Fx(x(k))Δx(k)= −F(x(k))

(7)

yazılır. Burada Δx^(k)= x^(k+1) − x^(k) veya x^(k+1)= x^(k) + Δx^(k) dır.

Denklem takımı için Newton-Raphson algoritması:

1. Başlangıçta F(x) = 0 için x⁽⁰⁾ değerlerinin çözüm olduğunu varsayalım.
2. k = 0, 1, 2, …, m iterasyonlarında, Δx^(k), x^(k+1) ve F(x^(k+1)) değerlerini hesaplayın. Eğer |F(x^(k+1))| < ε_e ve |x^(k+1) − x^(k)| < ε_s ise durun. x^(k+1) aranılan sonuçtur (ε_e denklem hata toleransı ve ε_s ise çözüm tolerans vektörleridir). Eğer |F_x(x^(k+1))| = 0 ve F(x^(k+1)) ≠ 0 ise, kökler için yeni bir tahmin yapıp birinci basamağa dönülür. Aksi takdirde 3. basamakla devam edilir.
3. k + 1 değerlerini k olarak ele alıp 2. basamağa dönülür. Eğer bu işlem m defa yapıldığı halde |F(x^(k+1))| < ε_e veya |x^(k+1) − x^(k)| < ε_s sağlanamadı ise, çözüm bulunamamıştır. Algoritmanın durdurulması gerekir. İşleme yeni bir x⁽⁰⁾ tahmin vektörü ile yeniden başlanabilir veya farklı bir yöntem denenebilir.

Örnek:

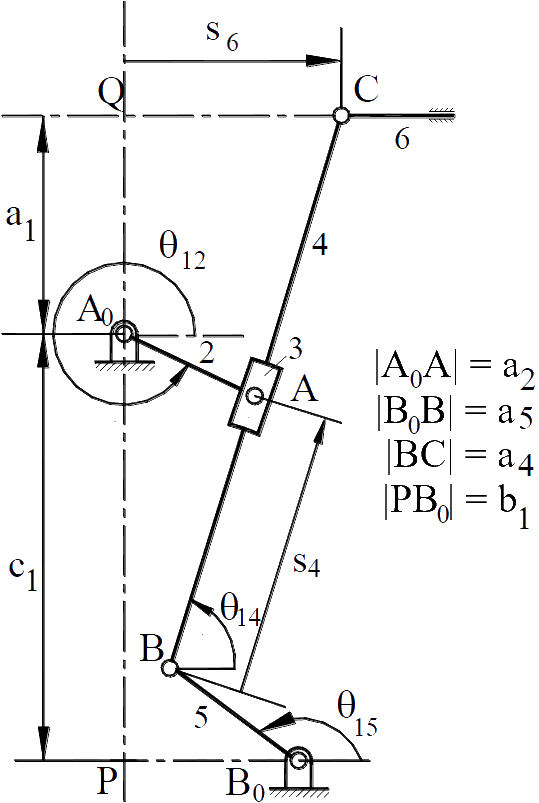
Newton-Raphson algoritmasını göstermek için aşağıdaki şekilde görülen mekanizmayı ele alalım. Bu mekanizmanın bilinmeyen konum değişkenlerini belirlemek için deneme yanılma yapmadan verecek kapalı denklemler elde etmemiz mümkün değildir. Karmaşık sayılar ile devre kapalılık denklemleri:

a₂e^iθ₁₂ = b₁ − ic₁ + a₅e^iθ₁₅ + s₄e^iθ₁₄

a₅e^iθ₁₅ + a₄e^iθ₁₄ = −b₁ + ia₁ + s₆

şeklindedir. Bu denklemler:

b₁ − ic₁ − a₂e^iθ₁₂ + a₅e^iθ₁₅ + s₄e^iθ₁₄ = 0

b₁ − ia₁ − s₆ + a₅e^iθ₁₅ + a₄e^iθ₁₄ = 0

olarak yazılabilir.

veya reel sayılarla:

b₁ − a₂cosθ₁₂ + a₅cosθ₁₅ + s₄cosθ₁₄ = 0

−c₁ − a₂sinθ₁₂ + a₅sinθ₁₅ + s₄sinθ₁₄ = 0

b₁ − s₆ + a₅cosθ₁₅ + a₄cosθ₁₄ = 0

−a₁ + a₅sinθ₁₅ + a₄sinθ₁₄ = 0

denklemleri elde edilir (karmaşık sayılar kullanarak denklemlerin karmaşık eşlenikleri kullanarak da dört denklem elde edilebilir. Bu örnekte reel sayılar kullanılacaktır). Elde edilen denklem takımı:

F₁(θ₁₄, θ₁₅, s₄) = 0

F₂(θ₁₄, θ₁₅, s₄) = 0

F₃(θ₁₄, θ₁₅, s₆) = 0

F₄(θ₁₄, θ₁₅) = 0

şeklindedir. Verilen θ₁₂ değerine göre bilinmeyen konum değişkenleri: θ₁₄, θ₁₅, s₄ ve s₆ değerlerini bulmak istiyoruz. Bu konum değişkenlerinin değeri olarak başlangıçta yapabileceğimiz ilk tahminler: θ₁₄⁰, θ₁₅⁰, s₄⁰, s₆⁰ olsun. Bu değerleri devre kapalılık denklemlerine yerleştirir isek denklemler sıfıra eşit olmayacak, her biri ε_i gibi bir farklı değerlere eşit olacaktır. Bu değerin küçük olması bizim çözüme ne kadar yakın olduğumuzun göstergesidir. θ₁₄¹ , θ₁₅¹, s₄¹, s₆¹ değerleri ise aranılan çözüm için daha iyi bir tahmin ise, ve δs₄ = s₄¹ − s₄⁰, δs₆ = s₆¹ − s₆⁰, δθ₁₄= θ₁₄¹ − θ₁₄⁰, δθ₁₅ = θ₁₅¹ − θ₁₅⁰ değerleri bu iki tahmin arasında fark olduğu kabul edilir ise bu fark Newton-Raphson algoritmasına göre denklem (7) kullanılarak:

\displaystyle \left[ {\begin{array}{cccc} {\text{i}{{\text{s}}_{4}}{{\text{e}}^{{\text{i}{{\text{θ}}_{{14}}}^{\text{k}}}}}} & {\text{i}{{\text{a}}_{5}}{{\text{e}}^{{\text{i}{{\text{θ}}_{{15}}}^{\text{k}}}}}} & {{{\text{e}}^{{\text{i}{{\text{θ}}_{{14}}}^{\text{k}}}}}} & 0 \\ {\text{i}{{\text{a}}_{4}}{{\text{e}}^{{\text{i}{{\text{θ}}_{{14}}}^{\text{k}}}}}} & {\text{i}{{\text{a}}_{5}}{{\text{e}}^{{\text{i}{{\text{θ}}_{{15}}}^{\text{k}}}}}} & 0 & {-1} \\ {-\text{i}{{\text{s}}_{4}}{{\text{e}}^{{-\text{i}{{\text{θ}}_{{14}}}^{\text{k}}}}}} & {-\text{i}{{\text{a}}_{5}}{{\text{e}}^{{-\text{i}{{\text{θ}}_{{15}}}^{\text{k}}}}}} & {{{\text{e}}^{{-\text{i}{{\text{θ}}_{{14}}}^{\text{k}}}}}} & 0 \\ {-\text{i}{{\text{a}}_{4}}{{\text{e}}^{{-\text{i}{{\text{θ}}_{{14}}}^{\text{k}}}}}} & {-\text{i}{{\text{a}}_{5}}{{\text{e}}^{{-\text{i}{{\text{θ}}_{{15}}}^{\text{k}}}}}} & 0 & {-1} \end{array}} \right]\left[ {\begin{array}{c} {\text{δ} {{\text{θ}}_{{14}}}} \\ {\text{δ} {{\text{θ}}_{{15}}}} \\ {\text{δ} {{\text{s}}_{4}}} \\ {\text{δ} {{\text{s}}_{6}}} \end{array}} \right]=-\left[ {\begin{array}{c} {{{\text{b}}_{1}}-\text{i}{{\text{c}}_{1}}-{{\text{a}}_{2}}{{\text{e}}^{{\text{i}{{\text{θ}}_{{12}}}^{\text{k}}}}}+{{\text{a}}_{5}}{{\text{e}}^{{\text{i}{{\text{θ}}_{{15}}}^{\text{k}}}}}+{{\text{s}}_{4}}{{\text{e}}^{{\text{i}{{\text{θ}}_{{14}}}^{\text{k}}}}}} \\ {{{\text{b}}_{1}}-\text{i}{{\text{a}}_{1}}-{{\text{s}}_{6}}^{\text{k}}+{{\text{a}}_{5}}{{\text{e}}^{{\text{i}{{\text{θ}}_{{15}}}^{\text{k}}}}}+{{\text{a}}_{4}}{{\text{e}}^{{\text{i}{{\text{θ}}_{{14}}}^{\text{k}}}}}} \\ {{{\text{b}}_{1}}+\text{i}{{\text{c}}_{1}}-{{\text{a}}_{2}}{{\text{e}}^{{-\text{i}{{\text{θ}}_{{12}}}^{\text{k}}}}}+{{\text{a}}_{5}}{{\text{e}}^{{-\text{i}{{\text{θ}}_{{15}}}^{\text{k}}}}}+{{\text{s}}_{4}}{{\text{e}}^{{-\text{i}{{\text{θ}}_{{14}}}^{\text{k}}}}}} \\ {{{\text{b}}_{1}}+\text{i}{{\text{a}}_{1}}-{{\text{s}}_{6}}^{\text{k}}+{{\text{a}}_{5}}{{\text{e}}^{{-\text{i}{{\text{θ}}_{{15}}}^{\text{k}}}}}+{{\text{a}}_{4}}{{\text{e}}^{{-\text{i}{{\text{θ}}_{{14}}}^{\text{k}}}}}} \end{array}} \right]

denklem takımından (karmaşık sayılar ile) veya:

\displaystyle \left[ {\begin{array}{cccc} {-{{\text{s}}_{4}}\sin {{\text{θ}}_{{14}}}^{k}}&{-{{\text{a}}_{5}}\sin {{\text{θ}}_{{15}}}^{\text{k}}}&{\cos {{\text{θ}}_{{14}}}^{\text{k}}}&0 \\ {{{\text{s}}_{4}}\cos {{\text{θ}}_{{14}}}^{\text{k}}}&{{{\text{a}}_{5}}\cos {{\text{θ}}_{{15}}}^{\text{k}}}&{\sin {{\text{θ}}_{{14}}}^{\text{k}}0}&0 \\ {-{{\text{a}}_{4}}\sin {{\text{θ}}_{{14}}}^{\text{k}}}&{{{\text{a}}_{5}}\sin {{\text{θ}}_{{15}}}^{\text{k}}}&0&1 \\ {{{\text{a}}_{4}}\cos {{\text{θ}}_{{14}}}^{\text{k}}}&{{{\text{a}}_{5}}\cos {{\text{θ}}_{{15}}}^{\text{k}}}&0&0 \end{array}} \right] \left[ {\begin{array}{c} {\text{δ} {{\text{θ}}_{{14}}}} \\ {\text{δ} {{\text{θ}}_{{15}}}} \\ {\text{δ} {{\text{s}}_{4}}} \\ {\text{δ} {{\text{s}}_{6}}} \end{array}} \right]=-\left[ {\begin{array}{c} {{{\text{b}}_{1}}-{{\text{a}}_{2}}\cos {{\text{θ}}_{{12}}}^{\text{k}}+{{\text{a}}_{5}}\cos {{\text{θ}}_{{14}}}^{\text{k}}+{{\text{s}}_{4}}\cos {{\text{θ}}_{{14}}}^{\text{k}}} \\ {-{{\text{c}}_{1}}-{{\text{a}}_{2}}\sin {{\text{θ}}_{{12}}}^{\text{k}}+{{\text{a}}_{5}}\sin {{\text{θ}}_{{14}}}^{\text{k}}+{{\text{s}}_{4}}\sin {{\text{θ}}_{{14}}}^{\text{k}}} \\ {{{\text{b}}_{1}}-{{\text{s}}_{6}}^{\text{k}}+{{\text{a}}_{5}}\cos {{\text{θ}}_{{15}}}^{\text{k}}+{{\text{a}}_{4}}\cos {{\text{θ}}_{{14}}}^{\text{k}}} \\ {-{{\text{a}}_{1}}+{{\text{a}}_{5}}\sin {{\text{θ}}_{{15}}}^{\text{k}}+{{\text{a}}_{4}}\sin {{\text{θ}}_{{14}}}^{\text{k}}} \end{array}} \right]

denklem takımından (reel sayılar ile) elde edilebilir. Dikkat edilir ise, denklem takımı bilinmeyen farklara göre lineer olup:

Aδ = E

şeklinde yazılabilir. A “katsayı matrisi” (Jacobian) reel veya karmaşık şekilde olabilir. ε_i elemanlarından oluşan E = [ε₁ ε₂ ε₃ … ε_n]^T kolon vektörü ise, konum değişkenlerinin ilk tahmin değerleri ile devre kapalılık denklemlerini hesapladığımızda ortaya çıkan denklem hatasıdır (yani her bir denklem sıfır olmayıp farklı bir ε_i değeri alacaktır ve bu da devrenin kapalı olmadığını gösteren hata değerleridir). Bu denklem takımından daha iyi olacağını beklediğimiz tahmin ile o an yaptığımız tahmin arasında fark ise:

δ = A^-1E

olarak çözebiliriz. Bu fark değerleri, kullanmakta olduğumuz örnekte δθ₁₄, δθ₁₅, δs₄ ve δs₅ olsun. Bu durumda konum değişkenleri için bir sonraki etapta yapacağımız daha iyi tahmin:

s₄^(k+1) = s₄^k + δs₄

s₅^(k+1) = s₅^k + δs₅

θ₁₄^(k+1) = δ₁₄^k + δθ₁₄

θ₁₅^(k+1) = θ₁₅^k + δθ₁₅

olacaktır. Yukarıda açıklanmış olan işlem, istenildiği kadar tekrarlanabilir. Durma kriteri olarak |F(x^(k+1))| < ε_e veya |x^(k+1) − x^(k)| < ε_s kullanılabilir. Mekanizmalarda devre denklemlerinin çözümü sırasında genellikle çok küçük hata değerleri kullanılsa bile yaklaşık 10 etapta çözüm bulunabilmektedir. Bunun mümkün olmadığı durumlar mekanizmanın kilitlendiği veya kilitlenmeye yakın olduğu konumlar veya ilk yapmış olduğumuz tahminin gerçek konum değişkenlerine göre çok uzak olduğu durumlardır. Bir mekanizmanın ölçekli çizimi üzerinde gözle bile yapabileceğimiz ilk tahminler genel olarak uygun bir ilk tahmin olabilir.

Eğer mekanizma tüm bir çevrim için incelenecek ise, bu işlem her bir krank açısı için yapılmalı ve her bir krank açısında konum değişkenleri değerleri için tahminde bulunulmalıdır. Ancak uygulamada mekanizmanın birinci konumu için tahmin yapılması, ikinci konum, eğer mekanizma bağımsız parametresinin ufak bir değişimi sonucu oluşuyor ise (örneğin krank dönmesi iki konum arasında 10° az olduğunda), bir önceki konumda elde edilen konum değerlerini bir sonraki konum değişkenleri için tahmin edilen değerler olarak kullanılmasının mümkün olduğu görülmüştür. Bu farkların büyük olduğu durumlarda çözüm yakınsamayabilir veya mekanizmanın farklı bir montaj şekline (ilk konumdan bu şekle mekanizma sökülüp takılmadan getirilemez) yakınsama olabilir. Benzer bir şekilde Jacobian matrisinin sıfır veya sıfıra yakın olduğu durumlarda bazı sorunlar ortaya çıkabilir. Genellikle lineer olmayan denklemlerin çözümü sırasında karşılaşılan problemler aynen mekanizmaların çözümü içinde geçerlidir.

Bu yöntem çok genel olup düzlemsel veya uzaysal, kayar, döner veya kamalı silindir mafsallı her türlü mekanizma için kolayca uygulanabilir. Uzaysal mekanizmalar için elde edilecek olan denklem sayısı tabi ki daha fazla olacaktır. Aynı yöntem günümüzde kullanılmakta olan çeşitli mekanizma analiz programlarında da kullanılmaktadır.

Örnek:

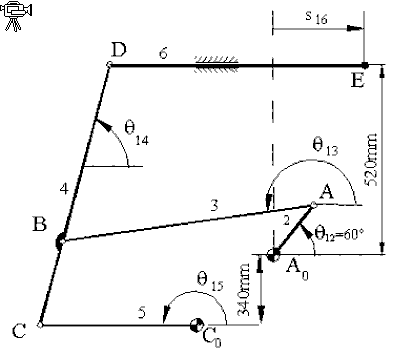
Yukarıda gösterilen mekanizmada uzuv boyutları: |C₀A₀|_y = a₁ = 340 mm; |A₀E|_y = b₁ = 520 mm; |C₀A₀|_x = d₁ = 623 mm; |A₀A| = a₂ = 250 mm; |AB| = a₃ = 1225 mm; |CB| = a₄ = 350 mm; |C₀C| = a₅ = 600 mm; |BD| = b₄ = 600 mm ve |DE| = a₆ = 1100 mm. θ₁₂ = 60° iken s₁₆ konum değişkeni değerini bulmak istiyoruz.

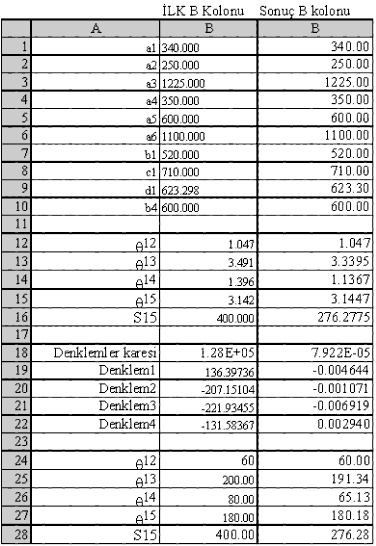
Mekanizmanın θ₁₂ = 60° konumunda, bilinmeyen konum değişkenleri için θ₁₃ = 200°, θ₁₅ = 180°; θ₁₄ = 80° ve s₁₆ = 400 mm değerlerini tahmin edelim. Tabi ki bu değerler devre kapalılık denklemlerini tam olarak sağlayamayacaktır. Bunun için Excel paket programının “Solver” (Çözücü) aracından yararlanacağız. Bu araç Newton-Raphson yöntemini kullanmaktadır.

Problemin çözümüne girmeden önce, Excelin “Options” (Seçenekler) menüsünden “Add-Ins” (Eklentiler) kısmı seçilir. Açılan pencerede Excel’e dahil edebileceğiniz çeşitli işlemler görüntülenecektir. Bunların içinden “Solver Add-In” (Çözücü Eklentisi) aktif değilse aktif hale getirilerek Excel’de kullanımı sağlanabilir. Excel’de “Data” (Veri) menüsü altında “Solver” (Çözücü) aracı görülür. Şimdi A1-A10 hücrelerine uzuv boyutları için kullandığımız adları ve B kolonunda karşı gelen hücrelere ise uzuv boyutların değerlerini yazalım. A12 hücresine bağımsız değişken adını ve B12 hücresine çözüm yapacağımız değerini (radyan cinsinden =60*pi()/180) yazalım. A13-A16 hücrelerine bağımlı değişken adlarını ve karşı gelen B hücrelerine bu giriş kolu açısı için bu değişkenler için tahminimizi (açılar radyan cinsinden) yazalım. B19-B22 hücrelerine değerleri sıfır olması gereken devre kapalılık denklemlerini yazalım. Bu hücrelerdeki denklemler:

Denklem 1:

a₂cosθ₁₂ + a₃cosθ₁₃ + d₁ − a₅cosθ₁₅ − a₄cosθ₁₄ = f₁ = 0

Excel’de yazılımı ise (B19 Hücresi):

=$B$2*COS(B12)+$B$3*COS(B13)+$B$9-$B$5*COS(B15)-$B$4*COS(B14)

Denklem 2:

a₂sinθ₁₂ + a₃sinθ₁₃ + a₁ − a₅sinθ₁₅ − a₄sinθ₁₄ = f₂ = 0

Excel’de yazılımı ise (B20 Hücresi):

=$B$2*SIN(B12)+$B$3*SIN(B13)+$B$1-$B$5*SIN(B15)-$B$4*SIN(B14)

Denklem 3:

a₂cosθ₁₂ + a₃cosθ₁₃ + b₄cosθ₁₄ + a₆ − s₁₆ = f₃ = 0

Excel’de yazılımı ise (B21 Hücresi):

=$B$2*COS(B12)+$B$3*COS(B13)+$B$4*COS(B14)+$B$6-B16

Denklem 4:

a₂sinθ₁₂ + a₃sinθ₁₃ + b₄sinθ₁₄ − b₁ = f₄ = 0

Excel’de yazılımı ise (B22 Hücresi):

=$B$2*SIN(B12)+$B$3*SIN(B13)+$B$4*SIN(B14)-$B$7

Eğer seçmiş olduğumuz bağımlı parametre değerleri doğru olsa idi, B19-B22 hücre değerleri sıfır olurdu. Tahminlerde hatalar olacağından bu değerler sıfır olmayacaktır. Solver aracını kullanmak için bu fonksiyonların karelerini alalım:

f = f₁² + f₂² + f₃² + f₄²

eğer f sıfır olur ise, diğer fonksiyon değerleri de sıfır olacaktır (Solver aracı bu şekilde çok değişkenli bir fonksiyonun minimum, maksimum değerini elde etmek veya belirli bir değer almasını sağlamak için kullanılabilir). Bu fonksiyonların kareleri toplamı B18 hücresine “=B19^2+B20^2+B21^2+B22^2” şeklinde yazılmıştır. B18 hücresinde iken “Data” (Veri) menüsünden önceden yüklemiş olduğumuz “Solver” (Çözücü) aracını seçelim. “Set Target Cell” (Hedef hücre belirle) olarak B18 hücresini ve “By changing cells” (değerleri değiştirilecek hücreler) olarak da B13-B16 hücrelerini işaretleyelim (bu hücrelerde sırası ile θ₁₃ = 200°, θ₁₄ = 80°, θ₁₅ = 180° (radyan olarak) ve s₁₆ = 400 değerleri bulunmaktadır). İkinci satırında “Equals to” ya (eşittir) karşılık “Value of” u (değeri) işaretleyip karşısında 0 değerin olmasını sağlayalım. “Options” (Seçenekler) tuşuna bastıktan sonra istediğimiz hata oranı, hassasiyet tolerans değerleri ile maksimum zaman ve iterasyon sayılarını değiştirebiliriz. Bu sayfayı “OK” tuşuna basıp kapattıktan sonra “Solve” (Çöz) komutuna bastığımızda B13-B16 değerlerini değiştirerek B18 hücresini sıfır yapmaya çalışacaktır. B18 hücresini sıfır yapan değerler tabi ki B19-B22 hücrelerini de sıfır yapacaktır. Aşağıda başlangıçta yazılmış olan ilk B kolonu ve “Solver” (Çözücü) aracı uygulandıktan sonra elde edilen sonuç B kolonu birlikte gösterilmektedir (Excel’de ilk B ve sonuç B kolonları aynı anda görünmez). Görüldüğü gibi denklemlerin karesinin toplamı başlangıçta 1.28×10⁶ iken sonuçta 7.92×10^-5 olmuştur. Devre kapalılık denklemini sağlayan bağımlı değişkenlerin değerleri: θ₁₃ = 191.34°, θ₁₄ =65.13°, θ₁₅ = 180.18° ve s₁₆ = 276.28 mm dir.