3.7 Karmaşık Sayılar Kullanılarak Konum Analizi

Karmaşık sayıların devre kapalılık denklemlerinde kullanılışlı olduğunu, genellikle polar gösterim ile devreyi oluşturan her bir vektörü karmaşık sayı kullanarak kolayca tanımlayıp gösterebileceğimizi görmüştük. Karmaşık sayılarla matematiksel işlemler normal sayılarla yapılan cebir işlemleri ile aynı olduğundan (tek bir fark i² = – 1 olacaktır), karmaşık sayılar aynı kolaylıkla mekanizmalarda konum parametrelerinin çözümü için kullanılabilir.

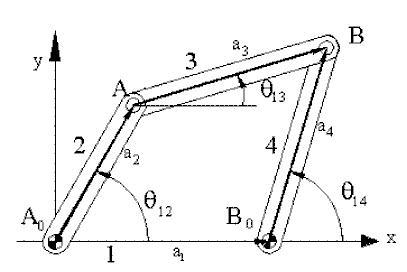
İlk örnek olarak dört-çubuk mekanizmasını ele alalım. Vektör devre denklemi

A₀A + AB = A₀B₀ + B₀B

olacaktır. Her bir uzva bağlı konum vektörünün uzunluğu a_j, pozitif x-ekseni ile yaptığı açı θ_1j dersek, karmaşık sayı olarak bu konum vektörü a_je^iθ_ij olarak gösterilebilir. Bu durumda devre kapalılık denklemi karmaşık sayılar ile:

a₂e^iθ₁₂ + a₃e^iθ₁₃ = a₁ + a₄e^iθ₁₄

(1)

Bu denkleminin reel ve sanal kısımları ayrı ayrı eşitlenerek üç konum parametresini (θ₁₂, θ₁₃ ve θ₁₄) içeren iki skaler denklem elde edilebilir. Konum parametrelerinden birisi bağımsız parametre olacağından iki bilinmeyenli iki denklem vardır. Bu denklemler:

a₂cosθ₁₂ + a₃cosθ₁₃ = a₁ + a₄cosθ₁₄

a₂sinθ₁₂ + a₃sinθ₁₃ = a₄sinθ₁₄

Bu iki denklemden verilen bir θ₁₂ açısı değerine göre θ₁₃ ve θ₁₄ değerlerini bulabilmek deneme-yanılma gerektirecektir. Bu denklemleri θ₁₃ ve θ₁₄ değerlerinin kolayca elde edilebilir hale getirmek gerekmektedir. İsterseniz bu skaler denklemleri kullanarak bu çözümü yapabilirsiniz.

Karmaşık düzlemde kalarak çözüm yapmak istediğimizde, mekanizma için geçerli olan ikinci bir denkleme ihtiyaç vardır. Bu denklemi elde etmek için Mekanizmanın devre denklemini yazdığımız eksen takımına göre, bir aynanın alt yüzeyini x-ekseni ile çakışacak şekilde yerleştirelim. Ayna üzerinde mekanizmanın görüntüsü görülecektir. Gerçek mekanizma hareket ettiği zaman aynadaki görüntü de hareket edecektir ve mekanizmanın oluşturduğu her bir kapalı devreye karşılık ayna görüntüde bir kapalı devre olacaktır.

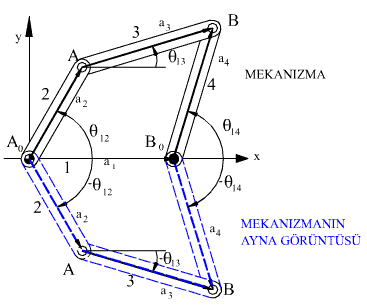
Gerçek devre ile görüntüde oluşan devrede vektörlerin boyutları aynı görülecek ancak gerçek mekanizmada saat yelkovanına ters yönde alınan açılar, ayna görüntüde saat yelkovanı yönünde olacaklardır. Bu görüntüde oluşan devre için, devre kapalılık denklemini yazdığımızda:

a₂e⁻ⁱ^θ₁₂ + a₃e⁻ⁱ^θ₁₃ = a₁ + a₄e^−iθ₁₄

(2)

Elde edilen bu ikinci denkleme devre kapalılık denkleminin sanal eşleniği denmektedir. (1) denkleminin geçerli olduğu her durumda bu sanal eşlenik de (2 denklemi) geçerlidir.

Karmaşık sayı düzleminde (1) ve (2) denklemleri iki konum değişkenini bulmak için kullanılabilir. (1) ve (2) denklemlerinin reel ve sanal kısımlarını ayrı ayrı eşitler ve skaler denklemler elde edersek, her iki denklemden elde edilecek olan denklemlerin aynı skaler denklemlere dönüştüğü görülecektir. Yakınsama yöntemi ile nümerik çözüm, ileride açıklanacaktır. Burada bilinmeyen konum parametrelerinden her biri bağımsız konum değişkeninin fonksiyonu olarak nasıl çözülebilir, onu görelim.

Dört çubuk mekanizmasında θ₁₄ değişkenini θ₁₂ parametresine göre çözmeyi hedefleyelim. Bu durumda θ₁₃ konum değişkenini 1 ve 2 numaralı denklemlerden yok etmemiz gereklidir. Devre kapalılık denklemi ve sanal eşleniğinden θ₁₃ ün yok edilmesi için yok etmek istediğimiz açıyı içeren terimi denklemin sol tarafına alarak yazalım:

a₃eⁱ^θ₁₃ = a₁ + a₄e^iθ₁₄ − a₂eⁱ^θ₁₂	(3)
a₃e⁻ⁱ^θ₁₃ = a₁ + a₄e^−iθ₁₄ − a₂e⁻ⁱ^θ₁₂	(4)

(yok edeceğimiz değişkeni içeren terim denklemin bir tarafına alınmıştır). (3) ve (4) denklemlerini taraf tarafa çarpar isek :

a₃²e^{i(θ₁₃ − θ₁₃)} = (a₁ + a₄e^iθ₁₄ − a₂eⁱ^θ₁₂)(a₁ + a₄e^−iθ₁₄ − a₂e⁻ⁱ^θ₁₂)

(5)

e^{i(θ − θ)} = eⁱ⁰ =1 olduğunu hatırlarsak:

a₃² = a₁² + a₄² + a₂² + a₁a₄[e^iθ₁₄ − e^−iθ₁₄] − a₁a₂[eⁱ^θ₁₂ + e⁻ⁱ^θ₁₂] − a₂a₄[e^{i(θ₁₄−θ₁₂)} − e^{−i(θ₁₄−θ₁₂)}]

(6)

Euler denklemine göre cosθ = (e^iθ + e^−iθ)/2 olacağından, (6) numaralı denklem:

a₃² = a₁² + a₂² + a₄² + 2a₁a₄cosθ₁₄ − 2a₁a₂cosθ₁₂ − 2a₂a₄cos(θ₁₄ − θ₁₂)

olacaktır. Bu denklem:

K₁cosθ₁₄ − K₂cosθ₁₂ + K₃ = cos(θ₁₄ − θ₁₂)

(7)

şeklinde yazılabilir. Burada K₁ = a₁/a₂ , K₂ = a₁/a₄ , K₃ = (a₁² + a₂² − a₃² + a₄² )/2a₂a₄ tür. (7) numaralı denkleme, bunu ilk tanımlayan kişiye atfen Freudenstein denklemi denmektedir. Bu denklem dört-çubuk mekanizmalarının sentezinde önemli rol oynar. θ₁₄ ve θ₁₂ değişkenleri arasında ilişki bu denklem ile belirlidir. Ancak verilen bir θ₁₂ değerine karşı gelen θ₁₄ açısını (7) numaralı denklemden kolayca belirlemek mevcut durumu ile mümkün değildir. Freudenstein denklemini

K₁cosθ₁₄ − K₂sinθ₁₂ + K₃ = cosθ₁₂cosθ₁₄ + sinθ₁₂sinθ₁₄

(8)

şeklinde yazabiliriz. t = tan(θ₁₄/2) ise

sinθ₁₄ = 2t/(1 + t²) ve cosθ₁₄ = (1 − t²)/(1 + t²)

olur. Bir açının yarısını kullanarak açının tüm trigonemetrik fonksiyonlarını sadece yarım açının tanjant fonksiyonu ile ifade edilmesi yarım tanjant yöntemi olarak bilinir). Bu durumda (8) denklemi:

At² + Bt + C = 0

(9)

olarak yazılabilir. Burada

A = cosθ₁₂(1 − K₂) + K₃ − K₁

B = −2 sinθ₁₂

C = cosθ₁₂(1 + K₂) + K₃ + K₁

dir. Dikkat edilirse, θ₁₂ bağımsız parametre değeri ve uzuv boyutları biliniyor ise A, B ve C parametre değerlerini hesaplayabiliriz. (9) numaralı denklem t’ye göre ikinci dereceden bir denklemdir ve çözümü

$\displaystyle \tan \left( {\frac{{{{\text{θ}}_{{14}}}}}{2}} \right)=\frac{{-\text{B}\pm \sqrt{{{{\text{B}}^{2}}-4\text{AC}}}}}{{2\text{A}}}$

dır. Bilinmeyen θ₁₄ açısı bu durumda

\displaystyle {{{\text{θ}}_{{14}}}=2{{\tan }^{{-1}}}\left[ {\frac{{-\text{B}\pm \sqrt{{{{\text{B}}^{2}}-4\text{AC}}}}}{{2\text{A}}}} \right]}

(10)

olur. (10) denklemi diskriminantın artı veya eksi işaret almasına göre iki değişik θ₁₄ değeri verecektir. Bu mekanizmanın iki farklı şekilde monte edilmesi ile ilgilidir.

Benzer yöntem kullanılarak devre kapalılık denkleminden θ₁₄ açısı yok edilerek θ₁₃ açısı için θ₁₂ ye göre aynı şekilde elde edilebilir (veya θ₁₂ değeri ile birlikte bu değere göre bulunan θ₁₄ açı değeri kullanılarak θ₁₃ açısı değeri bulunabilir). Montaj şekline göre uygulamada bir tanesi geçerli olacaktır. A, B ve C sadece uzuv boyutlarına ve bağımsız konum parametresi olan giriş kolu açısına bağlıdır. B² − 4AC < 0 ise, verilmiş olan kol açısında (θ₁₂) mekanizma monte
edilemez.

Denklem (8)’i θ₁₄ açısına göre çözmek için kullanılabilecek farklı bir yöntem için bu denklemi

(K₁ − cosθ₁₂)cosθ₁₄ − sinθ₁₄sinθ₁₂= K₂cosθ₁₂ − K₃

(11)

şeklinde yazalım. Ayrıca:

D cosϕ = K₁ − cosθ₁₂

D sinϕ = sinθ₁₂

(12)

der isek:

\displaystyle {\text{D}=\sqrt{{{{{\left( {{{\text{K}}_{1}}-\cos {{\text{θ}}_{{12}}}} \right)}}^{2}}+{{{\sin }}^{2}}{{\text{θ}}_{{12}}}}}=\sqrt{{1+{{\text{K}}_{1}}^{2}-2{{\text{K}}_{1}}\cos {{\text{θ}}_{{12}}}}}}

\displaystyle {\text{ϕ} ={{\tan }^{{-1}}}\frac{{\sin {{\text{θ}}_{{12}}}}}{{{{\text{K}}_{1}}-\cos {{\text{θ}}_{{12}}}}}}

(13)

olacaktır. Bu tanımlarla denklem (11):

Dcosϕcosθ₁₄ − Dsinϕsinθ₁₄ = K₂cosθ₁₂ − K₃

tür. cos (θ + ϕ) = cosθcosϕ − sinθsinϕ trigonometrik eşitliği kullanır isek:

cos(θ₁₄ + ϕ) = (K₂cosθ₁₂ − K₃)/D

(14)

veya

θ₁₄ = cos^-1[(K₂cosθ₁₂ − K₃)/D] − ϕ

(15)

(13) numaralı denklemin ϕ açısına göre çözümü sırasında açının doğru değerini bulmak için R-P tuşu veya ATAN2(x.y) fonksiyonunun kullanımı ihmal edilmemelidir. (15) numaralı denklemde ters kosinüs fonksiyonunun iki değişik değeri mekanizmanın iki farklı montaj şeklini verecektir.

Devre kapalılık denklemlerinin konum değişkenleri için çözümüne bir başka örnek olarak kol-kızak mekanizmasını ele alalım. Bu mekanizmada θ₁₂ bağımsız konum değişkeni, θ₁₄ ve s₄₃ ise bağımlı konum değişkenleridir. Amacımız her θ₁₂ açısına karşı gelen θ₁₄ değerini elde edebileceğimiz denklemi elde etmektir.

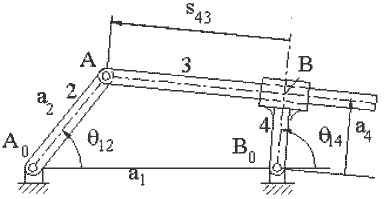
Vektör devre denklemi:

A₀A = A₀B₀ + B₀B + BA

olacaktır ve karmaşık sayılar ile yazıldığında:

a₂eⁱ^θ₁₂ = a₁ + a₄e^iθ₁₄ + s₄₃e^{i(θ₁₄ + π/2)}

veya

a₂eⁱ^θ₁₂ = a₁ + a₄e^iθ₁₄ + is₄₃e^iθ₁₄

(1)

Bu denklemin karmaşık eşleniği (mekanizmanın ayna görüntüsünde devre denklemi):

a₂e⁻ⁱ^θ₁₂ = a₁ + a₄e⁻ⁱ^θ₁₄ − is₄₃e⁻ⁱ^θ₁₄

(2)

olacaktır. s₄₃ parametresini bu iki denklemden yok etmek için bunu ihtiva eden terimi tek başına bırakalım.

is₄₃e^iθ₁₄ = a₂eⁱ^θ₁₂ − a₁ − a₄e^iθ₁₄	(3)
is₄₃e⁻ⁱ^θ₁₄ = a₁ + a₄e⁻ⁱ^θ₁₄ − a₂e⁻ⁱ^θ₁₂	(4)

s₄₃ parametresini yok etmek için 3 denklemini e⁻ⁱ^θ₁₄ ve 4 denklemini eⁱ^θ₁₄ ile çarpıp birbirlerine eşitleyelim:

a₂e^{i(θ₁₂−θ₁₄)} − a₁e⁻ⁱ^θ₁₄ − a₄ = a₁eⁱ^θ₁₄ + a₄ − a₂e^{−i(θ₁₂−θ₁₄)}

veya

a₂[e^{i(θ₁₂−θ₁₄)} + e^{−i(θ₁₂ − θ₁₄)}]− a₁[eⁱ^θ₁₄ + e⁻ⁱ^θ₁₄] − 2a₄ = 0

(5)

eⁱ^θ + e⁻ⁱ^θ = 2cosθ olduğu hatırlanır ise:

a₂cos(θ₁₄ − θ₁₂) − a₁cosθ₁₄ − a₄ = 0

(6)

Denklem 6 yı kullanarak verilen bir θ₁₂ değerine göre θ₁₄ değerini çözmemiz için cos(θ₁₄ − θ₁₂) yi trigonometrik eşitlik kullanarak açalım:

a₂cosθ₁₄cosθ₁₂ + a₂sinθ₁₄sinθ₁₂ − a₁cosθ₁₄ − a₄ = 0

veya:

a₂(cosθ₁₂ − a₁)cosθ₁₄ + a₂sinθ₁₄sinθ₁₂ − a₄ = 0

olacaktır. Dört-çubuk mekanizması için elde edilmiş olan denklemde yapılmış olduğu gibi, cosθ₁₄ ve sinθ₁₄fonksiyonları t = tan(θ₁₄/2) ile gösterilerek gerekli basitlemeler yapıldığında:

At² + Bt + C = 0

(7)

bu denklemde:

A = a₁ − a₄ − a₂cosθ₁₂

B = 2sinθ₁₂

C = a₂cosθ₁₂− a₁ − a₄

Bu ikinci derece denklemin θ₁₄ açısı için çözümü kolayca yapılabilir. Genel olarak yarım tanjant yöntemi kapalı çözüm elde edilmesi için kuvvetli bir yöntem olarak görülmektedir (eğer istenilir ise dört-çubuk mekanizması için verilen ve (11)-(15) numaralı denklemlerle açıklanmış olan farklı yöntem de kullanılabilir).

Eğer s₃₄ konum değişkenini θ₁₂ ye göre bulmamız gerekiyor ise bu sefer θ₁₄ parametresini devre denkleminden yok etmemiz gerekecektir. Bu durumda devre kapalılık denklemi ve onun karmaşık eşleniği:

(a₄ + is₄₃)e^iθ₁₄ = a₂eⁱ^θ₁₂ − a₁

(a₄ − is₄₃)e^−iθ₁₄ = a₂e⁻ⁱ^θ₁₂ − a₁

şeklinde yazılabilir. Taraf tarafa çarpım yapıldığında θ₁₄ açısı yok edilecek ve s₄₃ için çözüm:

s₄₃² = a₁² + a₂² − a₄² − 2a₁a₂cosθ₁₂

olacaktır. Bu çözümleri elde ederken sin^-1, cos^-1, tan^-1 gibi ters trigonometrik fonksiyonlar kullanılır iken bu fonksiyonların iki değerli olduğu ve hesap makinesi, veya başka herhangi bilgisayar program paketinin bu değerlerden birini vereceğini, mekanizmanın bağlanış şekline göre hangi değerin geçerli olduğuna kullanıcı olarak bizim karar vermemiz gerektiği unutulmamalıdır.

Geometrik çözümde gördüğümüz gibi, uygulamada birçok çok uzuvlu mekanizma basit mekanizmaların bağlanması ile elde edilmiştir. Basit mekanizmalar için elde edilen bu çözümler daha karmaşık mekanizmaların çözümünde kolayca kullanılabilir.