4.1 VELOCITY AND ACCELERATION ANALYSIS – 2

General Plane Motion:

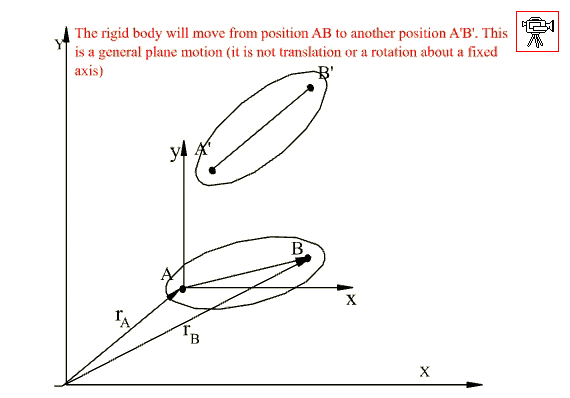
General plane motion is the plane motion which is neither  translation or rotation about a fixed axis but it can be analysed by the superposition of these motions using the relative motion concept.

Consider a plane represented by two points AB. Finite displacement of the rigid body from position 1 to position 2 at a time interval t can be regarded as the sum of the translation from AB to A’B” and a fixed axis of rotation about an axis perpendicular to the plane and passing through A’. One can also achieve the same final motion by translating from AB to A”B’ and then rotating about an axis passing through B’, or one can first perform a rotation about an axis perpendicular to the plane and passing through any point on the rigid body and then perform the translation. The actual paths of points will of course not correspond to the paths described by these different combinations of rotations and translations, but the final position can be reached and when the two positions are infinitesimally close these motions will coincide with the instantaneous paths of the points on the rigid body.

When performing translation, every point on the rigid body moves with the motion of the point selected and the velocity and acceleration of every point is the same for this motion. In case of rotation the rigid body is rotated about an axis passing through the particular point selected for translation. Now the rigid body is in a rotation. Since the point selected is not fixed, it is a relative motion.

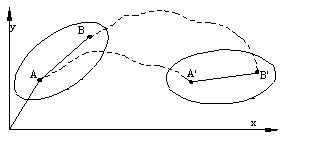
General Plane motion seperated to translation and rotation

Let us analyse this relative motion by attaching a moving reference frame x-y at point A,  that translates relative to the fixed frame X-Y .

The motion is to be considered of two parts. First, the body translates from AB to A’B” with displacement Dr _A which is the displacement of point A. This is similar to the rigid body translation discussed in part (a). Next the body rotates by an angle Df about A’. Since the distance of any other point, such as B, remains constant, the motion of B from B” to B’ will be on an arc with centre A’ and will be displaced by Dr _B/A. This displacement is the motion of point B relative to point A.

Δr_B = Δr_A +Δr_B/A

Since the motion from B” to B’ is a rotation, Dr _B/A = |BA|Df. Note that this relative motion is a function of absolute instantaneous angular motion Df of the rigid body. Therefore selection of point A will not effect this angular rotation, whereas the translation will depend on the point A that is selected. If one changes the order of rotation and translation the same equation will result. Dividing the above equation by the corresponding time interval, Dt and taking the limit as Dt tends to zero we obtain:

V_B = V_A+ V_B/A

where:

V_B/A = ω × r_B/A

and

 r _B/A = AB = r _B – r _A

V _B/Ais a relative velocity between two points B and A belonging to the same rigid body. V _B and V _Aare absolute velocities of points A and B on a rigid body in a general plane motion.

The same result can be obtained using complex numbers by writing the position of point B relative to A in complex numbers:

            r _B= r _A+be ^if

where b= |AB| and  f is the angle between the line AB and the positive real axis. b ^if term shows the position of point B with respect to A and b length is constant only if both A and B are on the same rigid body. Since we are to be concerned with the relative motion, let us assume that the velocity and acceleration of point A is known. (V _A  and a _Aare known). Differentiating the above equation with respect to time:

            V _B = V _A +ibwe ^if

where w=df/dt. The second term has the magnitude bw and is in the direction ie ^if   , which is a unit vector perpendicular to AB rotated in the sense of w. This is the relative velocity of point B with respect to A (Fig.4.60). Hence:

V _B/A = ibwe ^if

and

V _B = V _A + V _B/A

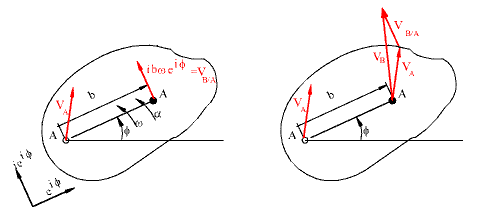
Velocity of point B in terms of velocity of point A

Differentiation of the velocity equation with respect to time yields:

a_B = a_A + ibαe^iϕ − bω²e^iϕ

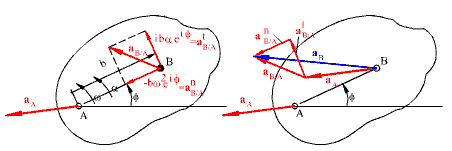
Acceleration of point B in terms of acceleration of point A

The first relative acceleration component has the magnitude ba and is in the direction ie ^if (Fig.4.61), which is perpendicular to the line AB and rotated in the sense of the angular acceleration a. This is relative acceleration component is tangential relative acceleration component and is denoted by a ^t _B/A . The second relative acceleration component has the magnitude bw² and is in the direction -e^if which is along the line AB towards the centre of rotation A. This direction is normal to the relative path of B with respect to A. Therefore it is called normal relative acceleration component and is denoted by a ⁿ _B/A. Hence the acceleration of point B can be expressed as:

a_B = a_A + a^t_B/A + aⁿ_B/A

and the relative acceleration is:

a_B/A= a^t_B/A + aⁿ_B/A

Therefore, for the relative motion between two points on a rigid body in a general plane motion the relative velocity and acceleration components are as if the body is in a fixed axis of rotation about one of the points on the rigid body.

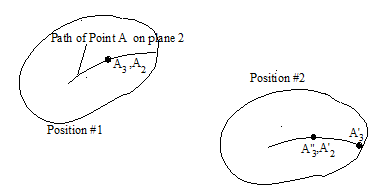
Another different type of relative motion occurs between two coincident points on two different rigid bodies but for which we know the path of one point relative to the other rigid body.

Consider plane 2 moved from position #1 to another position #2. During this time a point A₃  that is coincident with A ₂ at position #1 but on a different plane, moves to position A′₃ while A₂ moves to A′₂. Points that were instantaneously coincident in position #1 are not coincident at position #2. However, the path of on link 2 is known. The motion of point A₃ can be regarded as the sum of translation with A₃ to A″₃   that is coincident with A′₂  and a relative motion from A″₃ to A′₃ relative to the plane 2. Hence, as shown below, point A₃ first moves by a distance Dr_A2 with A₂ and then moves by a distance  Dr_A3/2 relative to A₂ . The order of the two superimposed motions is not important.

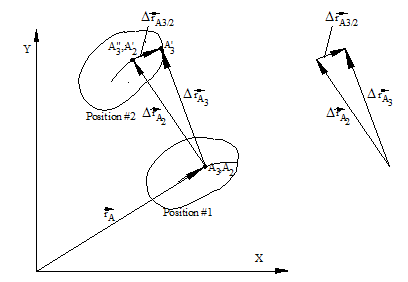
The total displacement of point A₃  is:

Δr_A3 = Δr_A2 + Δr_A3/2

Dividing the above expression by the corresponding time interval, Dt , and taking the limit as  Dt tends to zero, we obtain:

v_A3 = v_A2 + v_A3/2

where V_A3/2 is the relative velocity which is always tangent to the relative path of point A₃ with respect to the plane 2.

In mechanisms such relative motion occurs when we have prismatic, cylinder-in-slot or cam pairs between two moving links. In case of cam pairs we utilise equivalent linkage concepts with which we can replace a cam pair instantaneously by an equivalent mechanism containing lower kinematic pairs (see section 2.3). For prismatic or cylinder-in-slot joints, the relative path is a straight line.

In order to explain the relative motion between the two links, consider link 3 connected to link 2 by a prismatic joint . For simplicity, link 2 is connected to the fixed link by a revolute joint. Point B corresponds to two coincident points B₂ and B₃ on links 2 and 3. The position vector for point B (B₂ or B₃) in complex numbers is:

R_B = re^iθ

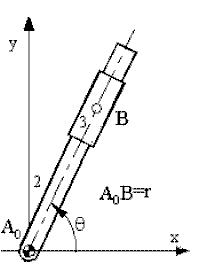
Note that R_B  is the position vector for both B₂ and B₃. However for B₂  r is a constant but for B₃ r is a variable. Therefore, when differentiating this vector, we must specify which rate of change of position is sought. For example if we are to determine the rate of change of the position of point B₂, then:

v_B2 = irωe^iθ

where w = dq/dt . If we want to determine the rate of change of the position B₃, then:

v_B2 = irωe^iθ + (dr/dt)e^iθ

The first term is the velocity of point B₂, V_B2. The second term is the relative velocity of point B₃ with respect to link 2. It is tangent to the relative path. Hence:

v_B3 = v_B2 + v_B3/2

B₃, which is fixed on link 3 will be coincident with another point B’₂ on link 2 after a certain time interval. The second derivative of the position vector with respect to time yields:

a_B3 = dv_B3/dt = [irαe^iθ − rω²e^iθ + i(dr/dt)ωe^iθ] + [(dr²/dt²)e^iθ + i(dr/dt)ωe^iθ]

Where the terms in the first bracket are those obtained from the differentiation of V_B2 , and those in the second bracket are obtained when the relative velocity V_B3/2  is differentiated. The first two terms are the tangential and normal accelerations components of point B ₂ and they add up to the angular acceleration of point B₂ (a_B2). The third term arises due to the fact that B₂ observed as the coincident point with B₃, will be a different point in a differential displacement. At a certain time interval  Dt, B₃ will be coincident with B’ ₂, that is at a distance  Dr from B₂ (direction being along the axis of the slider) . The velocity of B₂ is irωe^iθ and the velocity of B′₂ is  i(r + Δr)ωe^iθ. The change in the velocity during the time period  Dt is iΔrωe^iθ. Therefore there is an acceleration perpendicular to the slider axis by an amount irωe^iθ.

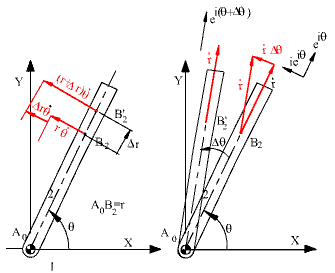
Consider the terms obtained when the relative velocity is differentiated. The first term is due to the change in magnitude of the relative velocity. This term is tangent to the relative path. The second term is due to the change in the direction of the relative velocity vector. In order to explain this term consider a constant magnitude for relative velocity. At a certain time interval Dt, link 2 will rotate by an angle Dq. The direction of the relative velocity is now e^{i(θ + Δθ)} instead of e^iθ initially. The vectorial change of the relative velocity vector is irΔθe^iθ, and its time rate of change is irΔθe^iθ.   The last two terms in both of the brackets are the same in magnitude and direction. They can be combined into one term 2irωe^iθ This term is called Coriolis acceleration component and is represented by a^c_B3/2 . It is a relative acceleration component. Its direction is normal to the relative path described by B₃ on link 2. Its direction is obtained by rotating the relative velocity vector V_B3/2, 90° in the sense of the angular velocity of link 2. Hence the acceleration of point B₃ can be written as:

a_B3 = irαe^iθ − rω²e^iθ + (dr²/dt²)e^iθ + 2i(dr/dt)ωe^iθ

a_B3 = a^t_B2 + aⁿ_B2 + a^t_B3/2 + a^c_B3/2

In the previous case, since the prismatic joint axis is along the radial line B₀B, the normal acceleration component of point B₂ (aⁿ₂) and the tangential relative acceleration component a^t_B3/2 are along the same direction (so is a^c_B3/2 and  a^t_B2). These directions need not be along the same direction in general. Consider a prismatic joint as shown in figure below between links 2 and 3. In such a case:

 r_B3 = ae^iθ + se^i(θ+β)

where b and a are fixed parameters of link 2. Differentiating, we obtain:

v_B3 = iaωe^iθ + isωe^i(θ+β) + (ds/dt)e^i(θ+β)

which can be written in the form:

v_B3 = iωe^iθ(a + se^iβ) + (ds/dt)e^i(θ+β)

Note that:

a + se^iβ = be^iγ

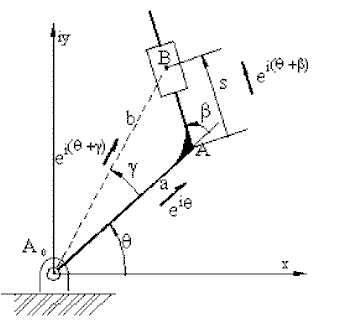
Where b is the variable distance A₀B and γ is the variable angle between A ₀A and A ₀B on link 2. This vector is the position of point B on a coordinate frame fixed on link 2. Hence:

v_B3 = iωbe^i(θ+γ) + (ds/dt)e^i(θ+β)

or

v_B3 = v_B2 + v_B3/2

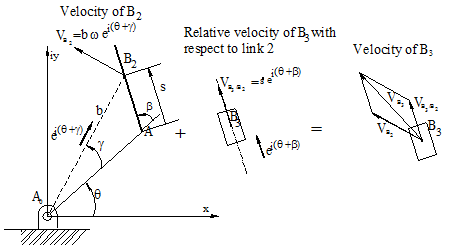
The first term has the magnitude ω|A₀B|= ωb and its direction is perpendicular to the line A₀B since the unit vector is ie^i(q+g) . The second term has the magnitude (ds/dt)  which is the relative velocity of point B₃ with respect to link 2 and its direction is along the slider axis AB given by the unit vector e^i(q+b ).

Differentiating the velocity equation once more, we have the acceleration of point B₃ as

a_B3 = iaαe^iθ − aω²e^iθ + isαe^i(θ+β) + i(ds/dt)ωe^i(θ+β) − sω²e^i(θ+β) + (d²s/dt²)e^i(θ+β) + i(ds/dt)ωe^i(θ+β)

the terms can be grouped as:

a_B3 = iα(a + se^iβ)e^iθ − ω²(a + se^iβ)e^iθ + 2i(ds/dt)ωe^i(θ+β)+ (d²s/dt²)e^i(θ+β)

or substituting a + se^iβ = be^iγ :

a_B3 = iαbe^i(θ+γ) − ω²be^i(θ+γ) + 2i(ds/dt)ωe^i(θ+β)+ (d²s/dt²)e^i(θ+β)

The first two terms are the tangential and normal acceleration components of point B₂ whose direction are normal and parallel (directed towards A₀) to the line A₀B respectively . The third term is the relative Coriolis acceleration which is perpendicular to the slider axis AB (given by the unit vector ie ^i(q+b) ). The last term is the tangential relative acceleration with magnitude d²s/dt² and direction e^i(q+b) which is along the slider axis AB. Therefore in vector form the acceleration of B₃ is:

a_B3 = a^t_B2 + aⁿ_B2 + a^c_B3/2 + a^t_B3/2