4.1 VELOCITY AND ACCELERATION ANALYSIS – 1

We can distinguish three types of plane motion:

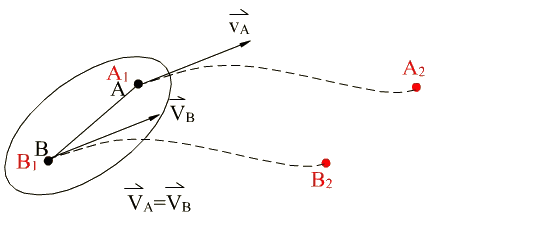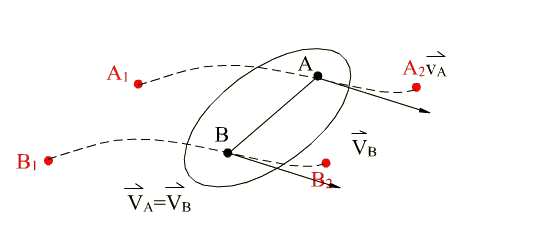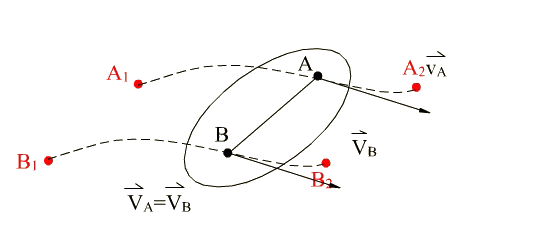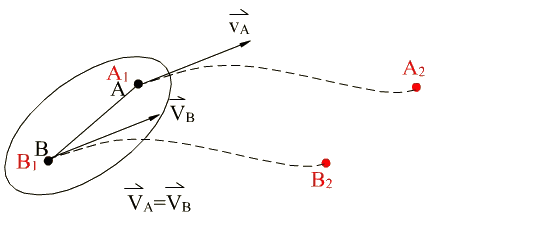
Translation:

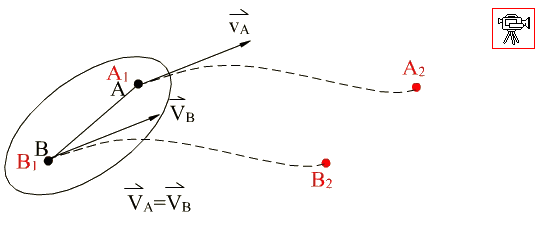
All points move along identically shaped paths such that a line taken on the rigid body always remains parallel to its original position (Fig.4.1). In such a case considering any two points A, B on the rigid body for a finite displacement from position 1 to position 2,  r_A1r_B1 = r_A2r_B2 . The position vector of point B, r _B will be given by:,

r_B = r_A + r_AB

The time rate of change of the position vector is the velocity of that point. Therefore:

\displaystyle \frac{{\text{d}{{\mathbf{r}}_{\mathbf{B}}}}}{{\text{dt}}}=\frac{{\text{d}{{\mathbf{r}}_{\mathbf{A}}}}}{{\text{dt}}}+\frac{{\text{d}{{\mathbf{r}}_{{\mathbf{AB}}}}}}{{\text{dt}}}

Since the vector AB is always parallel to its original position, its rate of change both in magnitude and direction is zero. Therefore:

\displaystyle \frac{{\text{d}{{\mathbf{r}}_{\mathbf{B}}}}}{{\text{dt}}}=\frac{{\text{d}{{\mathbf{r}}_{\mathbf{A}}}}}{{\text{dt}}} or V_A = V_B

We can take the second rate of change and noting that the second rate of change of the vector AB (r _AB) is zero:

\displaystyle \frac{{{{\text{d}}^{2}}{{\mathbf{r}}_{\mathbf{B}}}}}{{\text{d}{{\text{t}}^{2}}}}=\frac{{{{\text{d}}^{2}}{{\mathbf{r}}_{\mathbf{A}}}}}{{\text{d}{{\text{t}}^{2}}}} or a_A = a_B

Therefore the velocity and acceleration of every point on the rigid body will be equal at each instant if the rigid body is in a translation.

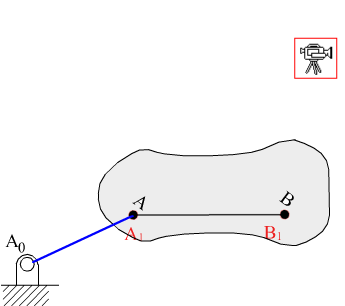
Rotation about a fixed axis :

Points on a rigid body move along circular arcs, concentric with the axis which is perpendicular to the motion  (Fig. 4.2). In the figure two finitely separated positions are shown. Note that:

∠AA₀A′ = ∠BB₀B′ = Δϕ

Every point will move in concentric circles with centre at O and the displacement of any point will be equal to the distance from that point to the centre of rotation times the angular displacement. Therefore:

Δr_A = r_AΔϕ     Δr_B = r_BΔϕ

and the time rate of change of the displacement:

\displaystyle \frac{{\text{Δ}{{\text{r}}_{\text{A}}}}}{{\text{Δt}}}={{\text{r}}_{\text{A}}}\frac{{\text{Δϕ}}}{{\text{Δt}}}          \displaystyle \frac{{\text{Δ}{{\text{r}}_{\text{B}}}}}{{\text{Δt}}}={{\text{r}}_{\text{B}}}\frac{{\text{Δϕ}}}{{\text{Δt}}}

In the limit when Dt goes to zero:

\displaystyle {\text{v}}_{\text{A}}={{\text{r}}_{\text{A}}}\frac{{\text{Δϕ}}}{{\text{Δt}}}        \displaystyle {\text{v}}_{\text{B}}={{\text{r}}_{\text{B}}}\frac{{\text{Δϕ}}}{{\text{Δt}}}

Where v_A and v_B are the magnitudes of the velocity vectors and ω = dϕ/dt is the angular velocity of the rigid body. The direction of the velocity vector of a point is perpendicular to line joining that point to the origin. This is conveniently expressed in vectorial notation:

v_A = ω × r_A

Where the operator (x) is the vectorial cross product.

We can as well use the complex number representation of the vectors and their time rate of change. For example in complex numbers the position vector of point A is (Fig.2.55):

r _A = r _A e ^iq

When the body is in a rotation, q is the variable angle and is a constant length. In this expression r _A  is the magnitude and  e^iq  is a unit vector in the direction of OA. Differentiating the position vector, we obtain:

V _A = ir _A w ^iq

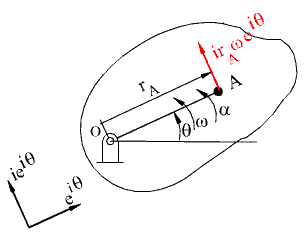
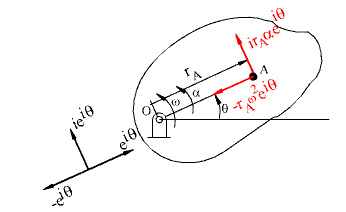
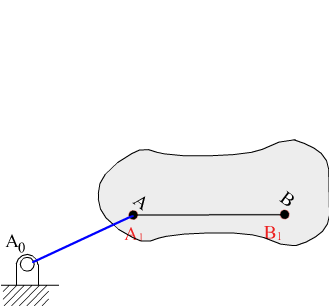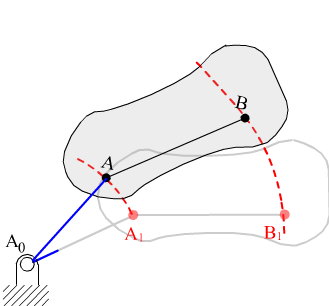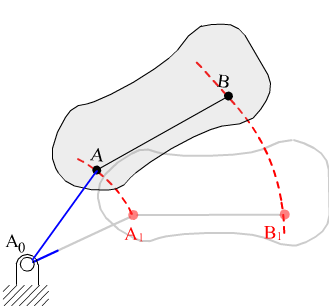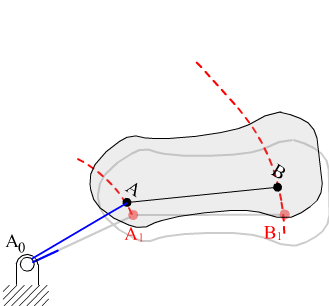
Velocity and acceleration of point A on the rigid body in rotation

Where:ω = dϕ/dt. The velocity vector has the magnitude r_A w and its direction is ie ^iq.   Since    i= e ^ip/2,   ie ^iq= e ^iq+p/2 . This new unit vector is perpendicular to OA.  The angular velocity is positive if the rate of change of q is counter clockwise and it is negative if there is a counter clockwise rate of change. Since the magnitude of the velocity vector is to be positive, if w is negative then the direction is -ie ^iq which is equal to e ^iq–p/2 . Hence we state that the direction of the velocity vector is perpendicular to OA and rotated in the sense of w. Differentiating the velocity vector to obtain the second rate of change of position:

\displaystyle {{\text{a}}_{\text{A}}}=\frac{{\text{d}{{\text{v}}_{\text{A}}}}}{{\text{dt}}}=\frac{\text{d}}{{\text{dt}}}\left( {\text{i}{{\text{r}}_{\text{A}}}{{\text{e}}^{{\text{iθ}}}}} \right)=\text{i}\frac{{\text{dω}}}{{\text{dt}}}{{\text{r}}_{\text{A}}}{{\text{e}}^{{\text{iθ}}}}-{{\text{r}}_{\text{A}}}{{\text{ω}}^{2}}{{\text{e}}^{{\text{iθ}}}}=\text{i}\text{α}{{\text{r}}_{\text{A}}}{{\text{e}}^{{\text{iθ}}}}-{{\text{r}}_{\text{A}}}{{\text{ω}}^{2}}{{\text{e}}^{{\text{iθ}}}}

where α = dω/dt = d²θ/dt².

The first term has the magnitude ar _A and is in the direction ie ^iq  which is perpendicular to OA and rotated in the sense of a (a is considered positive when the second rate of  change of q is counter clockwise). This acceleration component is tangent to the path of point A and its called the tangential acceleration. In general, it is expressed as a _A ^t. The second term has the magnitude r w ² and in the direction -e ^iq which is a unit vector opposite to the position vector r _A. It is known as the normal acceleration and expressed as a _A ⁿ. It is always directed towards the centre of curvature of the path drawn by the point under consideration. The tangential acceleration component and the velocity of a point will depend on the direction of angular acceleration and angular velocity. Where as the direction of normal acceleration is independent of the direction of the angular velocity or angular acceleration.

The acceleration of point A is expressed in terms of two components as.

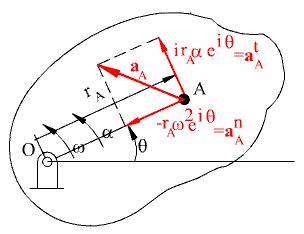
a_A = a_A^t + a_Aⁿ

The superscripts t and n refer to the tangential and normal components respectively. It must be noted that the centre of rotation 0 is the only point on the rigid body that has zero velocity and acceleration.

     In case of rotation about a fixed axis we can conclude:

• The velocity of every point is equal to the distance from that point to the axis of rotation times the angular velocity of the rigid body. The velocity vector is perpendicular to the line connecting the point to the axis of rotation and in the sense of angular velocity.
• The normal acceleration of every point  is equal to the distance from that point to the axis of rotation times the square of the angular velocity. The normal acceleration is always towards the axis of rotation along the line joining the point to the axis of rotation.
• Tangential acceleration of every point is equal to the distance from that point to the axis of rotation times the angular acceleration of the rigid body. The tangential acceleration vector is perpendicular to the line connecting the point to the axis of rotation and in the sense of angular acceleration.

The acceleration of a point on the rigid body is the vectorial sum of the tangential and normal acceleration components.