4.2 VELOCITY AND ACCELERATION ANALYSIS OF MECHANISMS-2

Example:

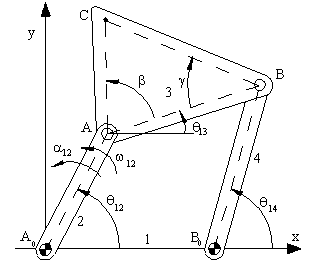
As for the velocity and acceleration analysis of a four-bar mechanism, a similar approach can be used. The loop closure equation and its complex conjugate is:

a₂e^iθ₁₂ + a₃e^iθ₁₃ = a₁ + a₄e^iθ₁₄

a₂e^−iθ₁₂ + a₃e^−iθ₁₃ = a₁ + a₄e^-iθ₁₄

The first derivative of the loop closure equation (velocity loop equation) is:

ia₂ω₁₂e^iθ₁₂ + ia₃ω₁₃e^iθ₁₃ = ia₄ω₁₄e^iθ₁₄

−ia₂ω₁₂e^−iθ₁₂ − ia₃ω₁₃e^−iθ₁₃ = −ia₄ω₁₄e^−iθ₁₄

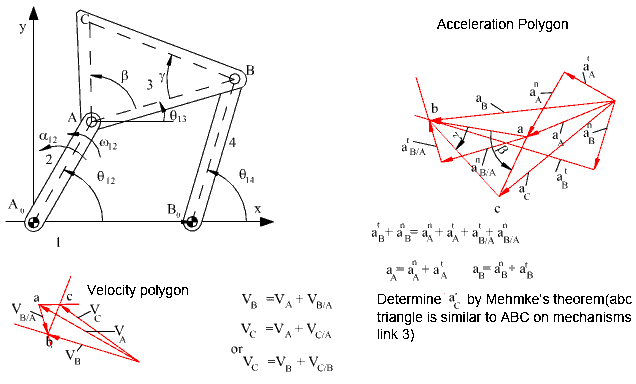
Note that the velocity loop equation in vector form is:

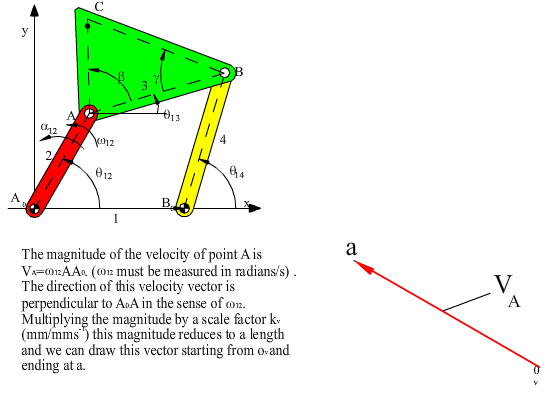
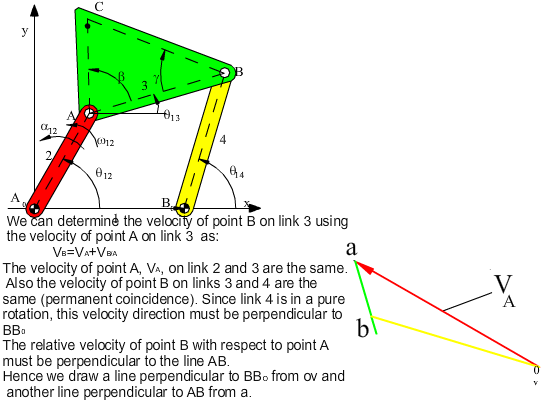
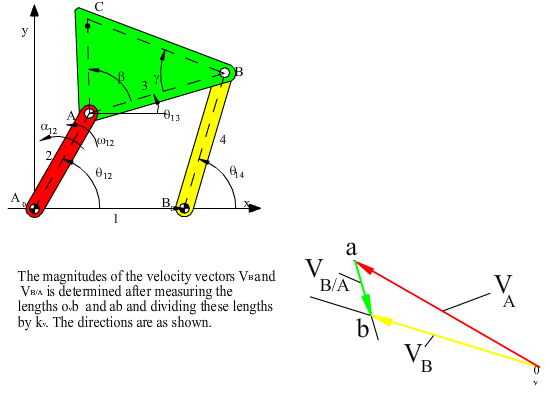
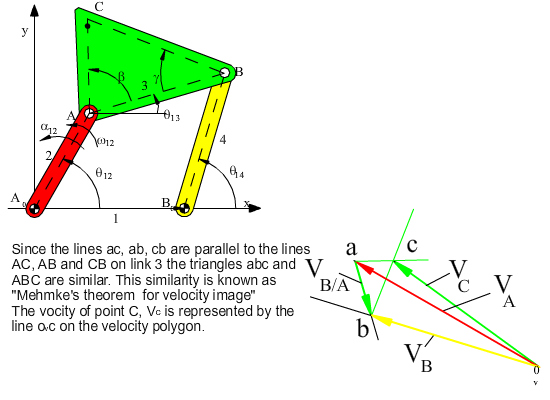
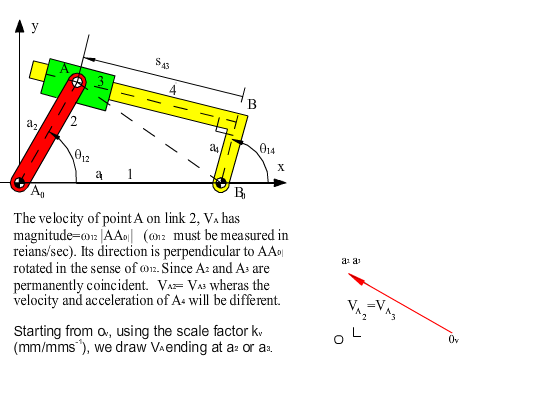
v_A + v_B/A = v_B

In complex numbers, the magnitude and direction of each velocity term can easily be identified. The velocity loop equation is a simple way of writing the velocity vector polygon. The velocity loop equation and its complex conjugate can be used to solve for the speed variables ω₁₃ and ω₁₄ for a given input speed ω₁₂, provided that the position variables θ₁₃ and θ₁₄ are solved for a given input angle θ₁₂:

\displaystyle {{\text{ω}}_{{13}}}=\frac{{\left| {\begin{array}{cc} {-{{\text{a}}_{2}}{{\text{ω}}_{{12}}}{{\text{e}}^{{\text{i}{{\text{θ}}_{{12}}}}}}} & {-{{\text{a}}_{4}}{{\text{e}}^{{\text{i}{{\text{θ}}_{{14}}}}}}} \\ {-{{\text{a}}_{2}}{{\text{ω}}_{{12}}}{{\text{e}}^{{-\text{i}{{\text{θ}}_{{12}}}}}}} & {-{{\text{a}}_{4}}{{\text{e}}^{{-\text{i}{{\text{θ}}_{{14}}}}}}} \end{array}} \right|}}{{\left| {\begin{array}{cc} {{{\text{a}}_{3}}{{\text{e}}^{{\text{i}{{\text{θ}}_{{13}}}}}}} & {-{{\text{a}}_{4}}{{\text{e}}^{{\text{i}{{\text{θ}}_{{14}}}}}}} \\ {{{\text{a}}_{3}}{{\text{e}}^{{-\text{i}{{\text{θ}}_{{13}}}}}}} & {-{{\text{a}}_{4}}{{\text{e}}^{{-\text{i}{{\text{θ}}_{{14}}}}}}} \end{array}} \right|}}=\frac{{{{\text{a}}_{2}}{{\text{a}}_{4}}\left( {{{\text{e}}^{{\text{i}\left( {{{\text{θ}}_{{12}}}-{{\text{θ}}_{{14}}}} \right)}}}-{{\text{e}}^{{-\text{i}\left( {{{\text{θ}}_{{12}}}-{{\text{θ}}_{{14}}}} \right)}}}} \right)}}{{{{\text{a}}_{3}}{{\text{a}}_{4}}\left( {-{{\text{e}}^{{-\text{i}\left( {{{\text{θ}}_{{14}}}-{{\text{θ}}_{{13}}}} \right)}}}+{{\text{e}}^{{\text{i}\left( {{{\text{θ}}_{{14}}}-{{\text{θ}}_{{13}}}} \right)}}}} \right)}}{{\text{ω}}_{{12}}}=\frac{{{{\text{a}}_{2}}}}{{{{\text{a}}_{3}}}}\frac{{\sin \left( {{{\text{θ}}_{{12}}}-{{\text{θ}}_{{14}}}} \right)}}{{\sin \left( {{{\text{θ}}_{{14}}}-{{\text{θ}}_{{13}}}} \right)}}{{\text{ω}}_{{12}}}

Similarly:

\displaystyle {{\text{ω}}_{{14}}}=\frac{{\left| {\begin{array}{cc} {{{\text{a}}_{3}}{{\text{e}}^{{\text{i}{{\text{θ}}_{{13}}}}}}} & {-{{\text{a}}_{2}}{{\text{ω}}_{{12}}}{{\text{e}}^{{\text{i}{{\text{θ}}_{{12}}}}}}} \\ {{{\text{a}}_{3}}{{\text{e}}^{{-\text{i}{{\text{θ}}_{{13}}}}}}} & {-{{\text{a}}_{2}}{{\text{ω}}_{{12}}}{{\text{e}}^{{-\text{i}{{\text{θ}}_{{12}}}}}}} \end{array}} \right|}}{{\left| {\begin{array}{cc} {{{\text{a}}_{3}}{{\text{e}}^{{\text{i}{{\text{θ}}_{{13}}}}}}} & {-{{\text{a}}_{4}}{{\text{e}}^{{\text{i}{{\text{θ}}_{{14}}}}}}} \\ {{{\text{a}}_{3}}{{\text{e}}^{{-\text{i}{{\text{θ}}_{{13}}}}}}} & {-{{\text{a}}_{4}}{{\text{e}}^{{-\text{i}{{\text{θ}}_{{14}}}}}}} \end{array}} \right|}}=\frac{{{{\text{a}}_{3}}{{\text{a}}_{2}}\left( {-{{\text{e}}^{{-\text{i}\left( {{{\text{θ}}_{{12}}}-{{\text{θ}}_{{13}}}} \right)}}}+{{\text{e}}^{{\text{i}\left( {{{\text{θ}}_{{12}}}-{{\text{θ}}_{{13}}}} \right)}}}} \right)}}{{{{\text{a}}_{3}}{{\text{a}}_{4}}\left( {-{{\text{e}}^{{-\text{i}\left( {{{\text{θ}}_{{14}}}-{{\text{θ}}_{{13}}}} \right)}}}+{{\text{e}}^{{-\text{i}\left( {{{\text{θ}}_{{14}}}-{{\text{θ}}_{{13}}}} \right)}}}} \right)}}{{\text{ω}}_{{12}}}=\frac{{{{\text{a}}_{2}}}}{{{{\text{a}}_{4}}}}\frac{{\sin \left( {{{\text{θ}}_{{12}}}-{{\text{θ}}_{{13}}}} \right)}}{{\sin \left( {{{\text{θ}}_{{14}}}-{{\text{θ}}_{{13}}}} \right)}}{{\text{ω}}_{{12}}}

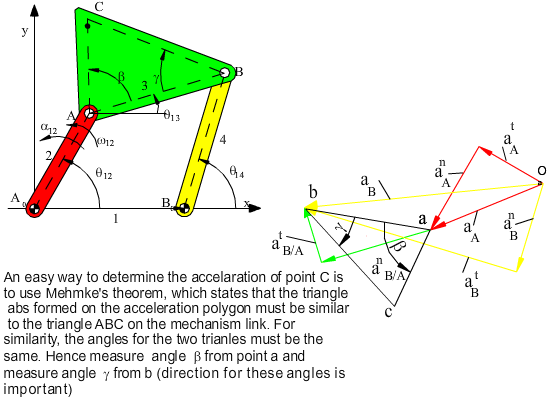
If the velocity of the coupler point C is to be determined, first wee need its position:

r_C = a₂e^iθ₁₂ + b₃e^{i(θ₁₃ + β)}

The derivative of the position vector will give us the velocity vector:

v_C = \displaystyle {\dot{\text{x}}} _C + i \displaystyle {\dot{\text{y}}} _C = ia₂ω₁₂e^iθ₁₂ + ib₃ω₁₃e^{i(θ₁₃ + β)}

which is the vector velocity equation:

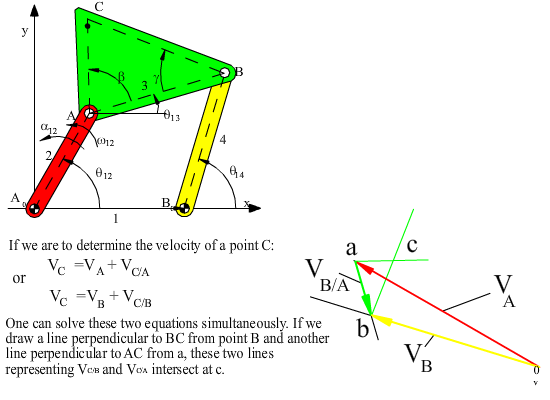
v_C = v_A + v_C/A

In terms of Cartesian components:

\displaystyle {\dot{\text{x}}} _C = −ia₂ω₁₂sinθ₁₂ − ib₃ω₁₃sin(θ₁₃ + β)

\displaystyle {\dot{\text{y}}} _C = a₂ω₁₂cosθ₁₂ + b₃ω₁₃cos(θ₁₃ + β)

If the position and the velocity loop equations are solved, one can easily determine the terms on the right hand side of the equations. Once the x and y components of the velocity is determined one can as well transform the velocity vector into polar form to yield the magnitude and direction by writing the velocity vector in the form:

v_C = v_Ce^iη

where v_C = \displaystyle \sqrt{{{{{\dot{\text{x}}}}_{\text{C}}}^{2}+{{{\dot{\text{y}}}}_{\text{C}}}^{2}}} = magnitude of velocity, and η = tan^-1( \displaystyle {\dot{\text{y}}} _C/ \displaystyle {\dot{\text{x}}} _C) = the angle the velocity vector makes with respect to positive x-axis.

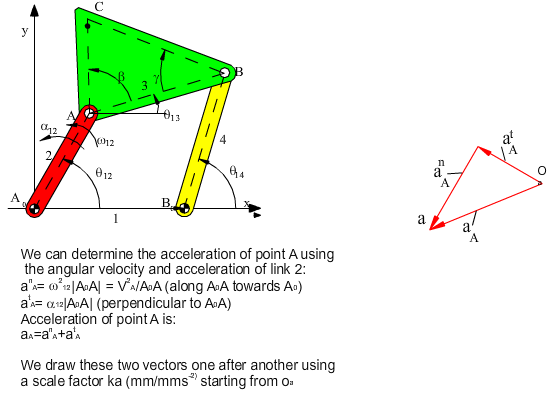
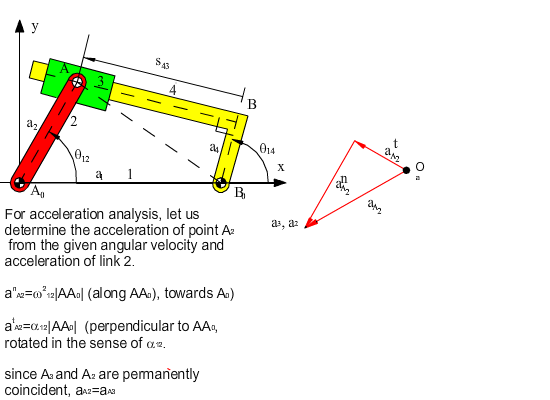
For the acceleration analysis, the second derivative of the loop closure equation (acceleration loop equation) is:

ia₂α₁₂e^iθ₁₂ − a₂ω₁₂²e^iθ₁₂ + ia₃α₁₃e^iθ₁₃ − a₃ω₁₃²e^iθ₁₃ = ia₄α₁₄e^iθ₁₄ − a₄ω₁₄²e^iθ₁₄

−ia₂α₁₂e^−iθ₁₂ − a₂ω₁₂²e^−iθ₁₂ − ia₃α₁₃e^−iθ₁₃ − a₃ω₁₃²e^−iθ₁₃ = −ia₄α₁₄e^−iθ₁₄ − a₄ω₁₄²e^−iθ₁₄

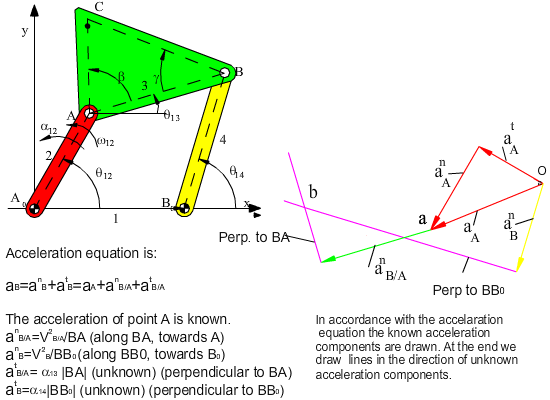
Note that the acceleration loop equation is nothing but the acceleration vector equation in the  form:

a^t_A + aⁿ_A + a^t_B/A + aⁿ_B/A = a^t_B + aⁿ_B

Rearranging the terms so that only the unknown acceleration variables are on the left hand side of the equation:

  ia₃α₁₃e^iθ₁₃ − ia₄α₁₄e^iθ₁₄ = −ia₂α₁₂e^iθ₁₂ + a₂ω₁₂²e^iθ₁₂ + a₃ω₁₃²e^iθ₁₃ − a₄ω₁₄²e^iθ₁₄

−ia₃α₁₃e^−iθ₁₃ + ia₄α₁₄e^−iθ₁₄ = ia₂α₁₂e^−iθ₁₂ + a₂ω₁₂²e^−iθ₁₂ + a₃ω₁₃²e^−iθ₁₃ − a₄ω₁₄²e^−iθ₁₄

Solving the two linear equations for the acceleration variables:

α₁₃ = \displaystyle \frac{{{{\text{a}}_{2}}{{\text{α}}_{{12}}}\sin \left( {{{\text{θ}}_{{12}}}-{{\text{θ}}_{{14}}}} \right)+{{\text{a}}_{2}}{{\text{ω}}_{{12}}}^{2}\cos \left( {{{\text{θ}}_{{12}}}-{{\text{θ}}_{{14}}}} \right)+{{\text{a}}_{3}}{{\text{ω}}_{{13}}}^{2}\cos \left( {{{\text{θ}}_{{13}}}-{{\text{θ}}_{{14}}}} \right)-{{\text{a}}_{4}}{{\text{ω}}_{{12}}}^{2}}}{{{{\text{a}}_{3}}\sin \left( {{{\text{θ}}_{{14}}}-{{\text{θ}}_{{13}}}} \right)}}

and

α₁₄ = \displaystyle \frac{{{{\text{a}}_{2}}{{\text{α}}_{{12}}}\sin \left( {{{\text{θ}}_{{12}}}-{{\text{θ}}_{{13}}}} \right)+{{\text{a}}_{2}}{{\text{ω}}_{{12}}}^{2}\cos \left( {{{\text{θ}}_{{12}}}-{{\text{θ}}_{{13}}}} \right)+{{\text{a}}_{3}}{{\text{ω}}_{{13}}}^{2}-{{\text{a}}_{4}}{{\text{ω}}_{{14}}}^{2}\cos \left( {{{\text{θ}}_{{13}}}-{{\text{θ}}_{{14}}}} \right)}}{{{{\text{a}}_{4}}\sin \left( {{{\text{θ}}_{{14}}}-{{\text{θ}}_{{13}}}} \right)}}

The acceleration of the coupler point C can be obtained from the second derivative of the position vector:

a_C = ia₂α₁₂e^iθ₁₂ − a₂ω₁₂²e^iθ₁₂ + ib₃α₁₃e^{i(θ₁₃ + β)} − b₃ω₁₃²e^{i(θ₁₃ + β)}

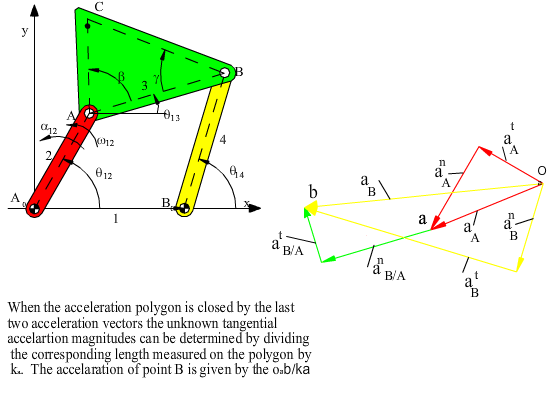
Hence, after the solution of the position, velocity and acceleration loop equations, one can easily determine the position, velocity and acceleration of any point in any one of the links of the mechanism. The graphical solution of the velocity and acceleration vector equations are as shown below.

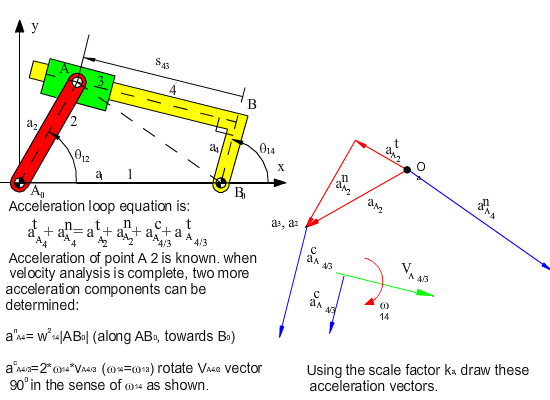
The velocity and acceleration loop equations are always linear in terms of the speed and acceleration variables. It is the solution of the loop equations that require more effort since they are nonlinear. The above procedure can be explained step by step as follows:

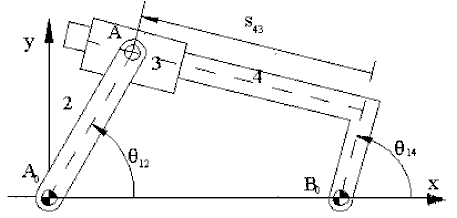
Consider the inverted slider-crank mechanism shown below. The loop closure equation was:

a₂e^iθ₁₂ = a₁ + a₄e^iθ₁₄ + is₄₃e^iθ₁₄

The velocity loop equation will be obtained by differentiating:

iω₁₂a₂e^iθ₁₂ = iω₁₄a₄e^iθ₁₄ − ω₁₄s₄₃e^iθ₁₄ + i \displaystyle {\dot{\text{s}}}₄₃e^iθ₁₄

or, regrouping terms:

iω₁₂a₂e^iθ₁₂ = iω₁₄(a₄ + is₄₃)e^iθ₁₄ + i \displaystyle {\dot{\text{s}}}₄₃e^iθ₁₄

 

This velocity loop equation is the velocity vector equation:

v_A2 = v_A3 = v_A4 + v_A3/A4

The first term is the velocity of point A₂ on link 2, whose magnitude is equal to the distance from the centre of rotation (|A₀A| = a₂) times the angular speed of link 2 (w₁₂). Since points A₂ and A₃ are permanently coincident points, their velocities are equal. The second term is the velocity of point A4 on link 4 whose magnitude is equal to the distance from the center of rotation (|B₀B| = a₄) times the angular speed of link 4 (w₁₄). The third term is the relative velocity of point A₃ with respect to link 4 whose direction is along the slider axis between links 3 and 4.

The acceleration loop equation is:

iα₁₂a₂e^iθ₁₂ − ω₁₂²a₂e^iθ₁₂ = iα₁₄(a₄ + is₄₃)e^iθ₁₄ − iω₁₄²(a₄ + is₄₃)e^iθ₁₄ + i \displaystyle {\ddot{\text{s}}}₄₃e^iθ₁₄ − 2 \displaystyle {\dot{\text{s}}}₄₃ω₁₄e^iθ₁₄

which is the acceleration vector equation:

a^t_A2 + aⁿ_A2 = a^t_A3 + aⁿ_A3 = a^t_A4 + aⁿ_A4 + a^t_A3/A4 + a^c_A3/A4

The tangential and normal components of points A₂ and A₃ are equal. The normal and tangential components of A₄ are along B₀A and perpendicular to B₀A respectively. The third term on the right hand side is the relative tangential acceleration which has the magnitude \displaystyle {\ddot{\text{s}}}₄₃ and along the slider axis. The last term is the Coriolis acceleration component with magnitude 2 \displaystyle {\dot{\text{s}}}₄₃ω₁₄ perpendicular to the slider axis.

Graphical velocity and acceleration analysis of the mechanism is shown for the position given below. Note that the velocity vector equation used is:

v_A4 = v_A3 + v_A4/3

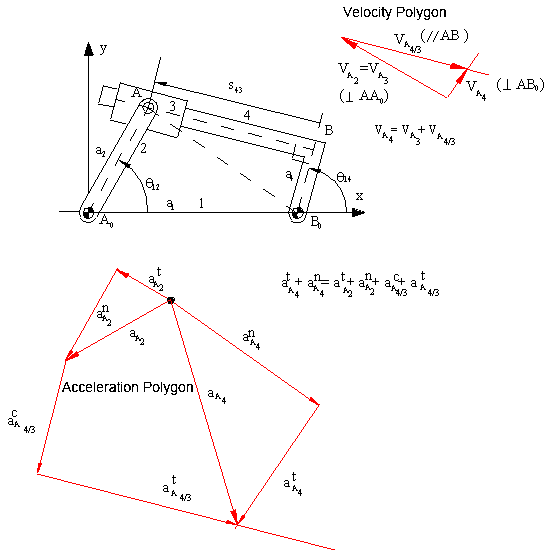
Since v_A3 = v_A2, the magnitude of this vector is |AA₀|ω₁₂. v_A4 is perpendicular to AB₀, v_A4/3 is parallel to the slider axis. First v_A3 is drawn using a certain scale. Then a line parallel to the slider axis is drawn from the tip of v_A3 and a line perpendicular to AB₀ is drawn from the starting point of v_A3. The intersection of these to lines gives the solution, the magnitude and the direction of v_A4 and v_A4/3 can be determined. When v_A4 is determined, ω₁₃ can be determined by dividing v_A4 with |AB₀| distance. From the velocity polygon we also note that ω₁₃ must be counter-clockwise for point A₄ to have the shown velocity direction.

For the acceleration analysis, the acceleration vector equation is rewritten as:

a^t_A4 + aⁿ_A4 = a^t_A3 + aⁿ_A3 + a^c_A4/3 + a^t_A4/3

so that there is one unknown on each side of the equation. We start with the known vector a^t_A3 = a^t_A2 (its magnitude is |AA₀|α₁₂, and its direction is perpendicular to AA₀ in the sense of α₁₂), and aⁿ_A3 = aⁿ_A2 (its magnitude is |AA₀|ω₁₂², and its direction is along AA₀, always directed to the centre of rotation, A₀). We draw these vectors using a certain scale k_a, Then we determine the magnitude and direction of Coriolis acceleration, a^c_A4/3. Its magnitude is 2ω₁₃v_A4/3 (the angular speed that changes the direction of the relative velocity must be used). The direction of coriolis acceleration is determined by rotating the relative velocity vector v_A4/3 by 90º in the sense of ω₁₃. After drawing a^c_A4/3, we draw a line tangent to the slider axis which is the direction of a^t_A4/3. Next, we consider the left hand side of the equation. We draw the normal acceleration aⁿ_A4 since its of magnitude is |AB₀|ω₁₃² (or = v_A4²/|AB₀|), and its direction is along AB₀ towards B₀. Then we draw a line normal to the line AB₀, which is the direction of a^t_A4 (of unknown magnitude). The point of intersection of the two lines is the solution of the acceleration polygon. This procedure is explained in step as follows:

In the following examples the displacement, velocity and acceleration analysis of some mechanisms will be shown with numerical values using graphical or analytical methods.