Example: The loop equations in a six link mechanism

In a mechanism we may have several loops and for each loop we may write one loop closure equation in vectorial form or in complex numbers. In Figure 1-A a six-link mechanism is shown. In order to have an open chain with no loops, one must disconnect two joints. The joint to be disconnected may differ, however the minimum number of joints to be disconnected is unique. When disconnecting the joint one must make sure that all the links are kept in an open chain (i.e. there should not be two open chains) When we disconnect the joints at C and B (Figure 1-B) there is no loop in the mechanism (one can as well disconnect D and E or D and A, etc. However, one cannot disconnect for example joints B and D. In such a case a link is disconnected from the chain. When we write the position of point C using the open chains 1, 2, 3 and 1, 5, 4 (while Joint B is disconnected), defining the necessary position variables we obtain the vector loop equation as:

A_oA + AC = A_oD_o + D_oE + EC

When we write the vector loop equation in complex numbers:

a₂e^iθ₁₂ + a₃e^iθ₁₃ = a₁ + a₅e^iθ₁₅ + a₄e^iθ₁₄

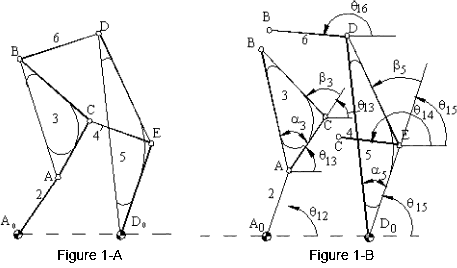
(a₁ = |A_oD_o|, a₂ = |A_oA|, a₃ = |AC|, b₁ = |AB|, c₃ = |CB|, a₄ = |EC|, a₅ = |D_oE|, b₅ = |D_oD|, c₅ = |ED|, a₆ = |BD|)

Similarly when we write the position of point B using open chains formed by the links 1, 2, 3 and 1, 5, 6 (Assuming Joint at C is disconnected), the vector loop equation we thus obtain is:

A₀A + AB = A₀D₀ + D₀D + DB

In complex numbers:

a₂e^iθ₁₂ + b₃e^{i(θ₁₃ + α₃)} = a₁ + b₅e^{i(θ₁₅ + α₅)} + a₆e^iθ₁₆

Note that the position of links 3 and 5 in the two vector loop equations are defined by different vectors (For link 3 vectors AC and AB, for link 5 vectors D₀E and D₀D). The magnitude of these vectors are fixed link dimensions and the angle between the two vectors on the same link is a constant angle. (α₃ and α₅). These angles are defined by the link dimensions. Hence the position of each link must be defined by only one angle position variable. (θ₁₃ and θ₁₅) .

In the two vector loop equations there are 5 position variables. (θ₁₂, θ₁₃, θ₁₄, θ₁₅ and θ₁₆). If one of the position variables is given as the input or independent position variable, then the other four position variables can be solved from the two vector loop equations (corresponding to four scalar equations).

If we connect the joint B after connecting joint C, then the loop we shall be forming when B is connected is ECBDE loop (links 4,3 and 5,6 open branches). In the previous case since Joint C was disconnected, when closing joint B we formed a loop A₀ABDD₀A₀. In this case the vector loop equation is:

EC + CB = ED + DB

In complex numbers:

a₄e^iθ₁₄ + c₃e^{i(θ₁₃ + β₃)} = c₅e^{i(θ₁₅ + β₅)} + a₆e^iθ₁₆

Consider the three vector loop equations. In this case the number of scalar equations obtained will exceed the number of unknown position variables. We know that the solution is possible only when the number of scaler equations is equal to the number of unknown parameters. Then the number of linearly independent vector loop equations cannot be greater than half of the number of unknown position variables. In other words, one of the three loop equations must be linearly dependant. In fact, if we add the vector loop equations one and three side by side:

A₀A + AC + EC + CB = D₀E + EC + ED + DB

Note that we can cancel the vector EC from both sides. Referring to the figure below three vectors on the same link have a fixed relationship between each other irrespective of the angle θ which determines the position of the link.

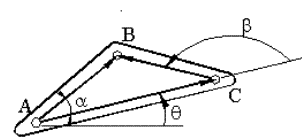
Since points A, B and C are on the same link:

b = |AB| , a = |AC|, c = |CB| lengths are constant

AB = be^{i(θ + α)}, AC = ae^iθ, CB = ce^{i(θ + β)} (AB, AC and CB vectors)

AC + CB = AB (The vector equation which will allways be true)

If we write this equation in complex numbers:

ae^iθ + ce^{i(θ + β)} = (a + ce^iβ)e^iθ = be^{i(θ + α)} = be^iαe^iθ

⇒  a + ce^iβ = be^iα

note that this equation is satisfied irrespective of the value of the variable angle θ. 

Hence for link 3 AC + CB = AB and for link 5 D₀E + ED = D₀D. Now if we add the first and the third loop closure equation, we end up with the second loop equation. Hence one of the loop closure equation is linearly dependent on the ther two loop equations. Only two equations can be used for the solution of the unknown position parameters.

 

A₀A + AC + CE = A₀D₀ + D₀E

A₀A + AB + BD = A₀D₀ + D₀D

a₂e^iθ₁₂ + a₃e^iθ₁₃ + a₄e^iθ₁₄ = a₁ + a₅e^iθ₁₅

a₂e^iθ₁₂ + b₃e^{i(θ₁₃ + α₃)} + a₆e^iθ₁₆ = a₁ + b₅e^{i(θ₁₅ + α₅)}

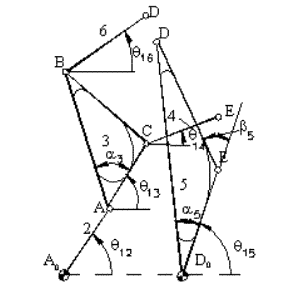
You can disconnect other joints to write the loop equations (e.g. D and E). When disconnecting these joints for the loop identification make sure that no link is separeted from the whole chain (every link is connected to another link by at least one joint). Also there must be no loop left. When different joints are disconnected you may define parameters to show the position of a link. However for the same link these different parameters will differ only by a constant angle. In every case the number of loop equations and the number of independent position parameters for a particular mechanism is the same. For example in the above example θ₁₄ = θ₁₄′ + π and θ₁₆ = θ₁₆′ + π.