3.1 KINEMATICS OF A PARTICLE

In order to determine the position of a point (particle) in plane, we must first locate a reference frame. For example, if we attach a coordinate frame to a moving body, the position of a point on the rigid body will be defined by constant dimensions. If our reference frame is attached to a fixed body or another body that is moving, the coordinates of a point on this rigid body will be variable. Once the reference frame is established, different co-ordinate systems (Cartesian or polar) and different parameters can be used to determine the position of a particle. In describing the location of a point (see Figure below).

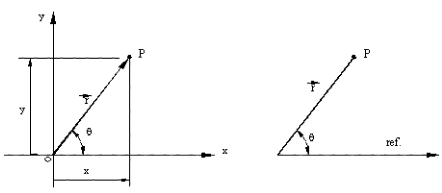
We must state the distance from the origin of the reference frame to point P and give the angular orientation of the line OP in the reference frame. These two specifications (the magnitude and direction) are the properties that define a vector. Therefore, the position of a particle (point) is given by a vector OP = r , This vector is commonly known as the position vector of a particle (point). The vector can be represented in Cartesian form as:

r = xi + yj

In this equation, i and j are the unit vectors and x and y are the distances in horizontal and vertical axes which are to be measured by a certain scale.

If polar form the position vector is:    r = r∠θ

Where r is the distance and θ is the inclination of the line OP from a reference line, measured in counter-clockwise direction. Usually this reference line is taken as the positive x axis of the Cartesian frame, so that the polar and Cartesian forms of representation can be easily interchanged.

conversion from x, y to r, θ or vice versa:

x = r cosθ          y = r sinθ         r = \displaystyle \sqrt{{{{\text{x}}^{2}}+{{\text{y}}^{2}}}}          θ = tan^-1(y/x)

For the determination of the position of a particle, we can also make use of complex algebra. Although complex numbers are not vectors, they can be used to represent position vectors in plane if the axes of the reference frame are used as the real and the imaginary axes of the complex plane (which is also known as the Gauss-Argand diagram). In such a case the position of a particle can be expressed in terms of a complex number z which is:

z = x + it

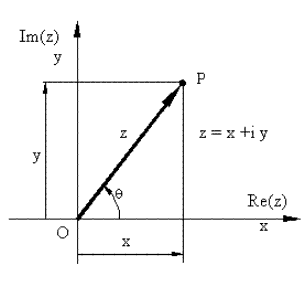
Where x and y are the distances measured along the real and imaginary axes and i is an operator which is defined as the unit imaginary number (i = \displaystyle {\sqrt{{-1}}} ) or 90° CCW rotation operator.

The detailed explanation of complex algebra is given in Appendix I The usefulness of complex numbers is due to the fact that the transformation from the Cartesian parameters (x, y) to the polar parameters (r, θ) or vice versa, can be performed with no additional burden. Since the complex number, z, which shows the position vector of a particle can be written as:

z = r cosθ + i r sinθ = r (cosθ + i sinθ)

Euler’s Equation:   e^iθ = cosθ + i sinθ

If we also make use of the Euler’s equation:

z = re^iθ =  r cosθ + i r sinθ

In the exponential form of the position vector re^iθ, (r) is the distance of point P to O (OP, which is the magnitude of the vector) and e^iθ is a unit vector along the direction of OP (e^iθ = cosθ + i sinθ).  In other words, In Gauss-Argand diagram if a number is multiplied by e^iθ it rotates by an angle θ in counterclockwise direction (Please refer to Appendix I).

In general the position of the particle will change in time (it is a function of time) This change can be expressed either using rectangular or polar coordinates. However if one of the parameters (r, θ) or (x, y) is constant, it may be simpler to use the corresponding form of representation.

Rather than showing vectors by an arrow, we shall represent the vectors and the complex numbers in bold case letters.