2.4 Grübler’s Equation

General degree-of freedom equation can be simplified for certain special cases and certain special conclusions can be derived. For the case that we are going to analyse, we have one degree of freedom (F = 1) planar (λ = 3) mechanisms that contain only prismatic and revolute joints (f_i = 1, ∑f_i = j). If we use these values in the general degree-of freedom equation, we have:

3l − 2j − 4 = 0

(1)

This equation is known as Grübler’s equation due to the person who first found it (This equation was found much before the general degree-of-freedom equation.

We can conclude the following for the mechanisms that satisfy Grubler’s equation:

1. The number of links in the mechanism must be even
   l and j are integers, whatever the value of j, 2j is an even number. Also (2j + 4) is an even number. Since 3l = 2j + 4, in order this equation to be true, 3l must be even. Since 3 is an odd number, multiplication with an even number can only give an even number. Therefore l must be even.
2. The number of binary links in the mechanism must be greater or equal to four.

If a number of links contain k kinematic elements, let us denote this number of links by l_k . We can not have l₁ (since there can be no link with one kinematic element). The total number of links, l, in the mechanism will then be equal to:

 

l = l2 + l3 + l4 + l5 + … + ln

(2)

or

3l = 3l2 + 3l3 + 3l4 + 3l5 + … + 3ln

(3)

(In this equation l₂ refers to the number of links with 2 kinematic elements- i.e. number of binary links-, l₃ is the number of links with three kinematic elements – i.e. ternary links- ,etc.).
The number of kinematic elements in the mechanism will be:

2l2 + 3l3 + 4l4 + … + nln = Number of Kinematic Elements

(4)

Since two kinematic elements are joined to form a kinematic pair:

2j = 2l2 + 3l3 + 4l4 + … + nln

(5)

If we now substitute eqs (3) and (5) into Grubler’s Equation (1):

l₂ − (l₄ + 2l₅ + 3l₆ + … + (n − 3)l_n) = 4

or

l₂ = 4 + P

where

P = l₄ + 2l₅ + 3l₆ + … + (n − 3)l_n

P is always a positive quantity. It can at most be zero, if all the links in the mechanism are binary or ternary links. Hence, the number of binary links (l₂) can at least be 4 if P = 0, otherwise it is greater than 4.

3.The number of kinematic elements in one link cannot be greater than half of the number of links in the mechanism.

 

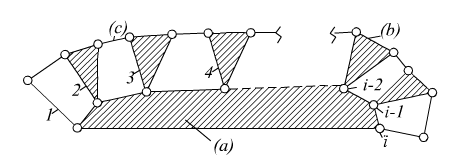
Consider a link (a) with i kinematic elements and let this number of kinematic elements be the maximum that a link can have. A kinematic chain using this link can be formed if we attach links of type (b) (see figure), and if we join these links with links of type (c). In this case the number of kinematic elements on link (a) will be a maximum. There will be 1 link of type (a) i links of type (b) and (i − 1) links of type (c). Then the number of links in this mechanism will be:

l = 1 + i + (i − 1)

or

i = l / 2

i is the maximum number of kinematic elements on any one link when the mechanism contains l links.