5.3 Mekanik Avantaj
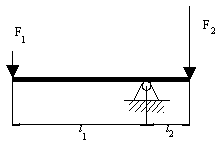
İlkokul yıllarından itibaren bildiğimiz basit levye prensibinde, şekilde gösterilen sistemde olduğu gibi, sistem dengede ise, dönme ekseninde moment toplamı sıfır olması gerekliliğinden:
F1l1 = F2l2 veya F2/F1 = l1/l2 = Mekanik Avantaj
olarak tanımlanmaktadır. Bu yöntemle yüksek F2 kuvvetini sınırlı bir F1 kuvveti ile elde etmek ister isek l1/l2 oranını yüksek seçmemiz gerekecektir. Buna bir farklı yaklaşım ise, kaybın olmadığını kabul ederek, enerji sakınımından birim zamanda yapılan iş ile elde edilen işin eşit olması şartından: F1v1 = F2v2 olacaktır. Burada v1 ve v2 kuvvetlerin etki ettiği noktada hızıdır.
Aynı kavramı mekanizmalarda uygular isek, örneğin bir dört-çubuk mekanizması için giriş momenti T12 ve çıkış kolu direnci T14 ise, enerji sakınımından dolayı (kayıplar ihmal edilerek):
Giriş Gücü = Çıkış Gücü
T12ω12 = T14ω14 veya Mekanik Avantaj = ma = T14/T12 = ω12/ω14 = |I14I24|/|I12I24|
olacaktır. Dikkat edilir ise mekanik avantaj hız oranının tersidir. Ayrıca, eğer giriş ve çıkış kollarına belirli bir kol boyunda bu kuvvetler uygulanıyor ise:
Mekanik Avantaj = ma = F14/F12 = (T14/r14)/(T12/r12) = (ω12r12)/(ω14r14) = (|I14I24|r12)/(|I12I24|r14)
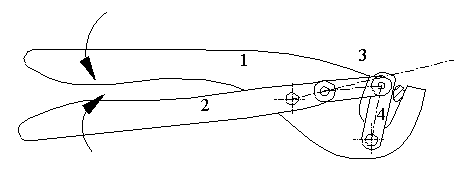
olacaktır. I14I24 = B0I24 uzunluğu sıfır olur ise mekanik avantaj sıfır olacak, I12I24 = A0I24 uzunluğu sıfır ise, mekanik avantaj sonsuz olacaktır. Tabi ki sistem elastikliğinden ve boşluklardan dolayı sonuçta mekanik avantaj sonsuz olamaz. Ancak mekanik avantaj çok yüksek değerlere ulaşacaktır. Bu şekilde basit levyelerle elde edilemeyecek kadar büyük mekanik avantaj elde edilebilecektir. Nitekim preslerde, sıkıştırma penslerinde, taş kırma gibi yüksek güç isteyen her işte yüksek mekanik avantaj sağlayan mekanizmalar kullanılmaktadır (aşağıdaki şekle bakınız).
Sonucun daha da genelleştirilmesi mümkündür. 1 uzvuna bağlı i ve j uzuvları olduğunda (i giriş, j ise çıkış uzvu olacaktır), bu iki uzvun hızı arasında (çakışan Iij ani dönme merkezinde bağıl hız sıfır olduğundan) ω1i|I1iIij| = ω1j|I1jIij| ilişkisinin olduğu belirlenmişti. Öyle ise, enerjinin sakınımı prensibi kullanıldığında
Mekanik Avantaj = ma = T1j/T1i = ω1i/ω1j = |I1jIij|/|I1iIij|
olacaktır (uzuvlara kuvvet uygulandığında denklemde uygun değişiklikler yapılır). Bu şekilde, mekanizmaların mekanik avantajlarının belirlenmesi hız oranlarının belirlenmesi problemine indirgenmiştir. Dikkat edilir ise, yüksek mekanik avantaj elde edilmesi için mekanizmanın ölü konumlara yakın olması gerekecektir.

Örnek:
Şekilde gösterilen perçin makinası için θ12 = 110° iken F16/T12 oranını bulun.
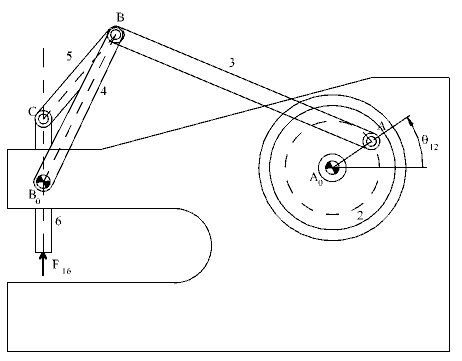
Mekanizma θ12 = 110° konumunda çizilmiştir. Sürtünme ihmal edildiğinde, enerjinin sakınımından dolayı :
T12ω12 = F16v16
yazabiliriz. 1, 2 ve 6 uzuvları arasında bulunan ani dönme merkezlerinden yararlanarak:
v16 = |I12I26|ω12
olacaktır. Öyle ise:
F16/T12 = ω12/v16 = ω12/(|I12I26|ω12) = 1/|I12I26|
dir. I12, A0 merkezidir. Bu durumda problem I26 ani dönme merkezini bulunması ile çözülecektir. Şekilde gösterildiği gibi, mafsal eksenleri dönme merkezleri olarak belirlendiğinde I26 ani dönme merkezini bulmak için ilk olarak I24 ve I46 ani dönme merkezlerini bulmamız gerekir. I24, I12I14 ile I32I34 doğrularının kesim noktası ve I46 ise I14I16 ile I45I56 doğrularının kesim noktası olarak belirlenir (kullanılan ani dönme merkezleri mafsal eksenleridir). Bu iki ani dönme merkezi belirlendikten sonra I26, I12I16 ile I24I46 doğrularının kesim noktasıdır. Dikkat edilir ise, I16 sonsuzda olduğundan I12I16 doğrusu A0 dan çizilen 1, 6 uzuvları arasındaki kayar mafsala dik bir doğrudur. I46 ise BC doğrusu (bu doğru I45I56 doğrusudur) ile B0 dan kayar mafsal eksenine dik doğrudur (I45I56 doğrusu). BC ile B0C doğruları çakıştığında B0 (I14) ile I26 çakışacaktır. Bu durumda I26 ani dönme merkezi ise, A0 (I12) ile çakışır. Aynı durum A0A ile AB doğrularının çakışması durumunda söz konusudur. Bu durumda I24, A0 noktası ile çakışacaktır. Bu durumda perçinleme sırasında I12I26 mesafesi çok kısa olacağından F16/T12 oranı büyük değerler alacaktır.
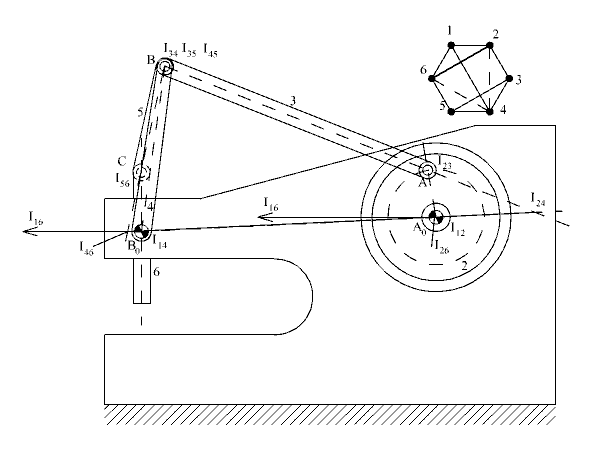
AutoCad kütüğü için tıklayınız: Mekanikpres.dwg.