Ani Dönme Merkezi

Önceki bölümlerde hız ve ivme analizinin bağıl hareket ile nasıl yapılabileceğini gördük ve bu yöntemi mekanizmaların analizi için geometrik veya analitik olarak kullanarak sonuçlar elde ettik. Sadece hız analizi için geçerli olan bir başka yöntem ise, dönme ve ötelemenin dışında kalan tüm genel düzlemsel hareketin bir dönme ile tanımlanabilmesidir. Bunun için şekilde gösterilen bir düzlemin iki genel konumunu ele alalım.Hareketi incelemeden önce belirli terimleri tanımlamamız gerekmektedir: Cismin birinci konumdan (AB) ikinci konuma (A′B′) sonlu uzaklıkta yerdeğişimi, P₁₂ olarak adlandıracağımız ve AA′ ile BB′ doğrularının orta dikmelerinin kesiştiği noktada yer alan nokta etrafında dönmesi ile sağlanabilir. Bunu temel bir teoremle ifade edelim:

  Chasles Teoremi (Şal teoremi olarak okunur):

Düzlemsel harekette bir cismin bir konumdan diğer sonlu uzaklıkta bir konuma hareketi en basit bir şekilde P₁₂ dönme polü etrafında bir dönme hareketi ile gerçekleştirilebilir. Dönme polü, P₁₂, cisim üzerinde alınan iki noktanın iki konumda bulundukları konumların orta dikmelerinin kesiştiği noktadır.

Rijit cismi bu yöntemle elde edilen P₁₂ merkezi etrafında döndürdüğümüzde, cismin rijit kalarak ikinci konuma varacağını ispat etmemiz gerekmektedir. Bunun için P₁₂ noktası sabit kalmak şartı ile, cismin üzerinde bulunan ABP₁₂ üçgeninin ikinci konumda A′B′P₁₂ üçgeni olduğunda birinci konumdaki üçgene (ABP₁₂) eşit olduğunu göstermemiz gerekir. Bu şekilde cisim şekil değişimine uğramamış olur. AB ve A′B′ kenarları rijit cisim üzerinde alınan aynı noktalar olduğundan eşittir. BP₁₂ ile B′P₁₂ kenarı ve AP₁₂ ile A′P₁₂ kenarları ise P₁₂ noktasının AA′ ve BB′ doğrularının orta dikmeleri üzerinde olmasından dolayı eşit olacaktır. Bu nedenle üçgenlerin üç kenarı birbirlerine eşit olduğundan, üçgenler eşittir. Bu durumda ∠AP₁₂A′ = ∠BP₁₂B′ = Δϕ = cismin iki konum arasında açısal dönmesidir.

Birinci konumdan ikinci konuma hareket en basit bir şekilde dönme ile olur ise de, genel düzlemsel hareketin bu dönme hareketine tam olarak eşdeğer olması şart değildir (öyle olsa idi, bu hareketi sabit bir eksen etrafında dönme olarak tanımlayıp genel düzlemsel hareket demezdik). Bu nedenle her hangi bir noktanın cismin genel düzlemsel hareketi sırasındaki yörüngesi ile cismin P₁₂ etrafında dönmesi ile elde edilen P₁₂ merkezli daire yayı yörüngesi arasında fark olacaktır. İki konum arasında bu iki değişik hareket, konumlar arası sonlu uzaklık kısaldıkça azalacaktır. İki konumun sonsuz yakın olması durumunda (limit durumu) her türlü düzlemsel hareket birinci dereceden bu dönme hareketine eşit olacaktır. Bu limit durumunda, orta dikmeler A ve B noktalarının yörüngelerine dik doğrulardır (Şekil aşağıda) (yörünge normalleri). Limit durumunda dönme polü ani dönme merkezi olarak adlandırılır (sentro, hız polü veya ani dönme polü terimleri bazı yayınlarda kullanılmaktadır).

yukarıda gösterilen şekilden:

|r_A|Δθ_A = |Δs_A|          ;          |r_B|Δθ_B = |Δs_B|          (r_A = IA ve r_B = IB)

Bu yer değişim Δt zaman aralığında olacaktır:

|r_A|Δθ_A/Δt = |Δs_A/Δt|          ;          |r_B|Δθ_B/Δt = |Δs_B/Δt|

Ancak Δθ_A = Δθ_B = Δϕ = rijit cismin dönme açısı olacağından ve Δt sıfıra giderken:

dθ_A/dt = dθ_B/dt = dϕ/dt = ω

Bu denklemde ω cismin açısal dönme hızıdır. Öyle ise, herhangi bir düzlemsel hareket bir an için bir ani dönme merkezi etrafında dönme yapıyor olarak düşünülebilir ve cismin üzerinde bulunan her hangi bir C noktasının hız vektörünün şiddeti :

|v_C| = ω|r_C| = ω|IC|

Bu denklemden yola çıkarak, düzlemsel hareket sırasında hareketli cisim üzerinde sadece ani dönme merkezinin hızının sıfır olduğu sonucuna varırız. Diğer noktaların, örneğin C noktasının, hız vektörünün yönü ise IC doğrusuna dik olup ω hız vektörünün yönüne bağlı olarak IC doğrusuna 90° saat yelkovanı yönünde veya ters yönünde dönmüştür. Vektörel olarak:

v_C = ω × r_C

yazılabilir. Burada × vektör çarpımıdır. ω z yönünde bir açısal hız vektörü olup r_C = IC vektörüdür.

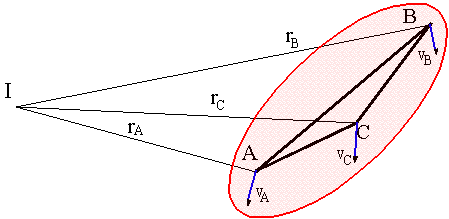
Ani dönme polü ve cisim üzerinde bulunan noktaların hızları

 Genel düzlemsel hareket için bu durumda varılacak sonuçlar şunlardır:

i)   Her düzlemsel hareket için, incelendiği anda geçerli olmak üzere, bir ani dönme merkezi bulunur. Bu nokta hareketli düzlemde o an için sıfır hıza sahip tek noktadır.

ii)  Cisim üzerinde bulunan her hangi bir noktanın hızının şiddeti o noktanın ani dönme merkezinden uzaklığının cismin açısal hızı ile çarpımıdır. Noktanın hızı noktayı ani dönme polüne bağlayan doğruya dik olup açısal hıza göredir.

iii) Hız analizi açısından her türlü düzlemsel hareket anlık olarak ani dönme merkezi etrafında dönme olarak düşünülebilir.