7.3 Kol-Kızak Mekanizması

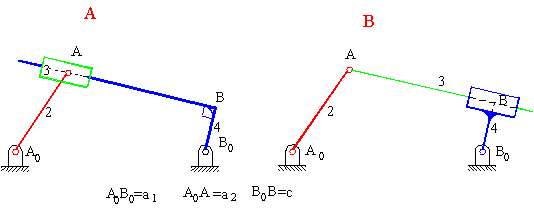
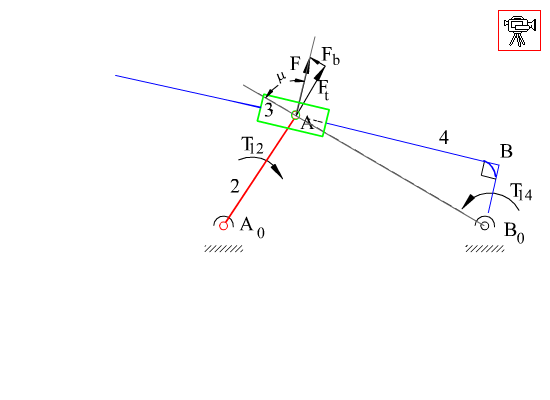
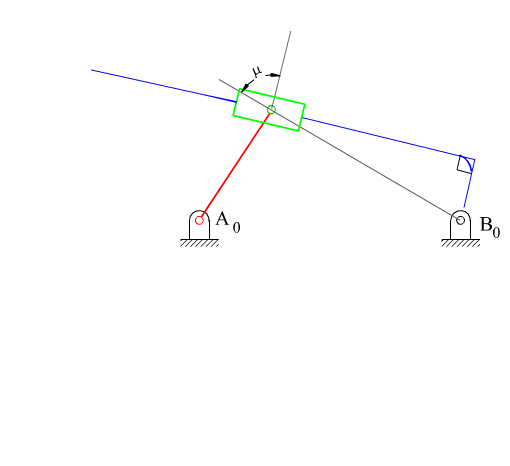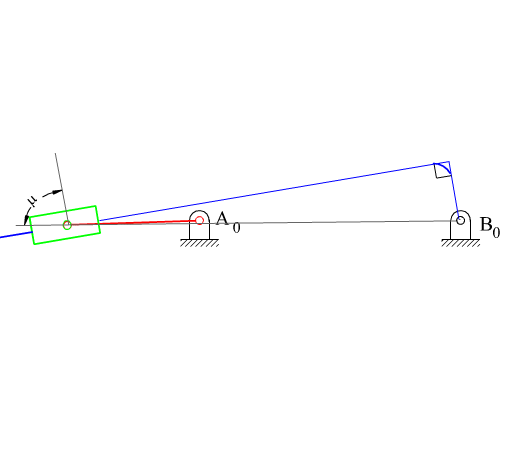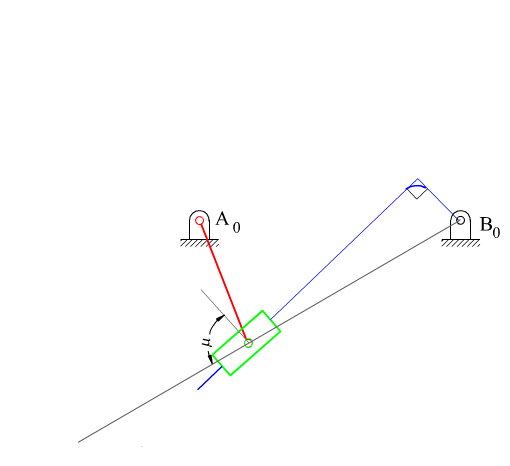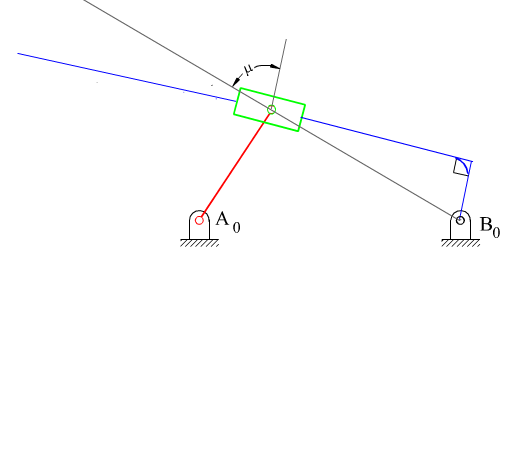
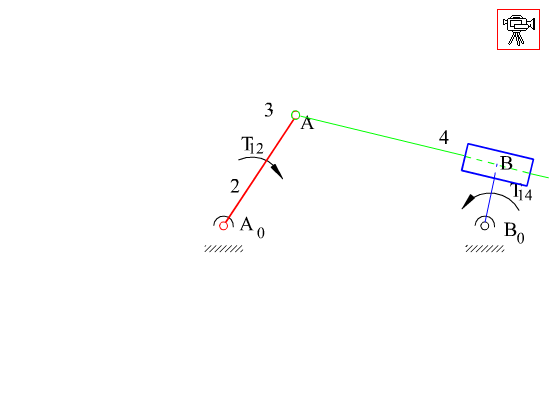
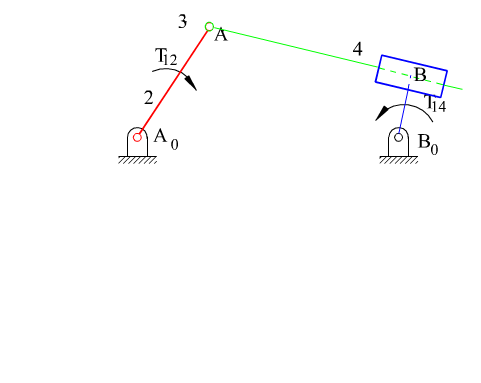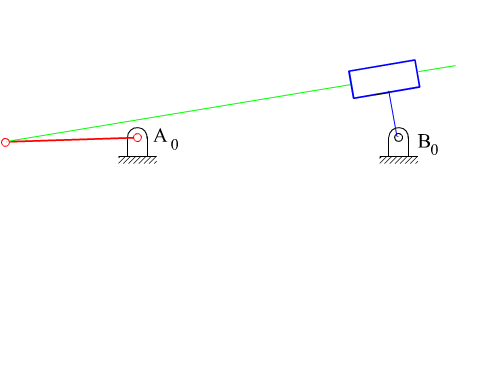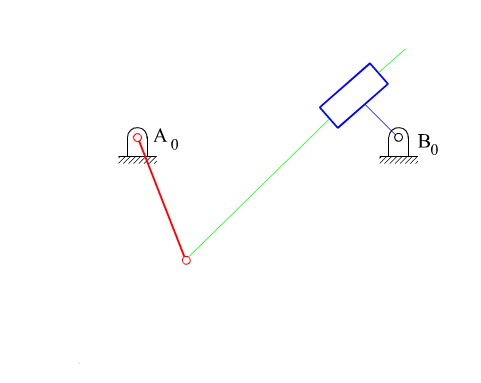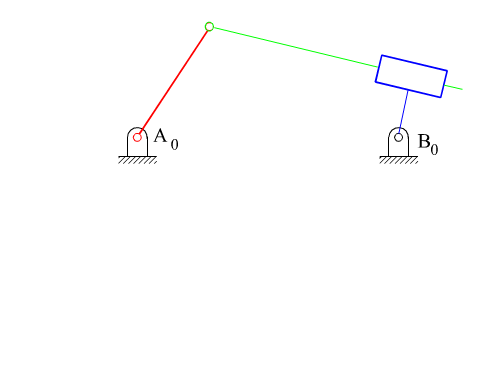
Kol-kızak mekanizması, krank-biyel mekanizmasında farklı bir uzvun sabit alınması ile kayar mafsalın sabit olmayan bir eksen yönünde öteleme yapmasıdır. Genel olarak yukarıda görüldüğü iki değişik yapıda olabilir. 2 uzvu giriş uzvu olup 4 uzvu çıkış uzvu olarak kullanım en yaygın uygulama şeklidir. Her iki değişik yapı içinde giriş uzvu ile çıkış uzvu dönme açıları arasında bağlantı aynı denklemle ifade edilir. Ancak bu iki değişik yapının kuvvet iletim özellikleri farklıdır.

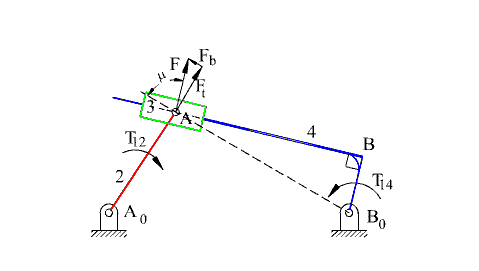
A da görülen yapı için bağlama açısının kritik değerleri yukarıda gösterilmiştir. F, dört uzvuna iletilen kuvvet, F_t ise bu kuvvetin çıkış kolunda moment yaratan bileşenidir. Bağlama açısının en küçük ve en büyük değerleri yine krank ile sabit uzvun aynı doğrultuda olduğu konumlardır B de gösterilen yapı için ise, 3 ve 4 uzuvları arasında moment iletimi söz konusudur ve önceden verilmiş olan bağlama açısı tanımı bu yapıda bir mekanizma için geçerli değildir (farklı bir tanım kullanılarak bağlama açısı tanımlanır ise de, bu kapsam dışında tutulacaktır).

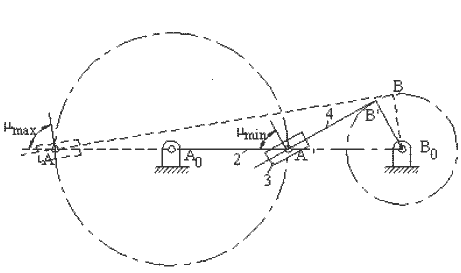
Kol-kızak mekanizması, BB₀ mesafesinin sıfır olup olmasına bağlı olarak santrik veya eksantriktir.

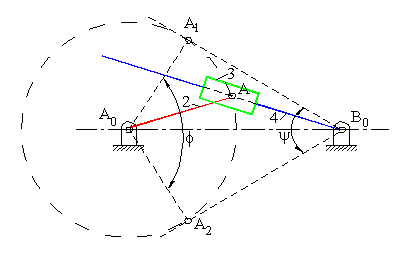
Santrik kol-kızak

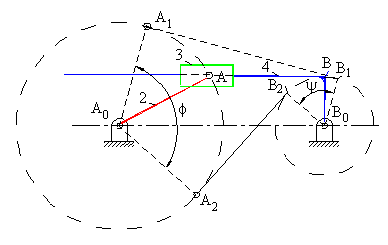
Eksantrik kol-kızak

Santrik kol-kızak mekanizmasının sınır konumları (sarkacın yön değiştirdiği konumlar, ölü konumlar), A₀ merkezli AA₀ yarıçaplı daireye B₀ dan teğetler çizilerek kolayca bulunur (Yukarıda A₀A₁B₀ ve A₀A₂B₀ konumları). Bu sınır konumlarda ∠A₀A₁B₀ = ∠A₀A₂B₀ = 90° olduğundan, salınım açısı (ψ) ile buna karşı gelen krank dönme açısı (ϕ) arasında

ψ + ϕ = 180°

(1)

bağıntısı vardır. Salınım yapan dört uzvunun bir yönde dönmesi sırasında krank ϕ açısı kadar dönerken, ters yönde krank 360° − ϕ açısı kadar dönecektir ve (1) denkleminden dolayı bu iki süre hiç bir zaman eşit değildir. Bu nedenle kol-kızak mekanizması vargel mekanizmalarında yüksek zaman oranı elde etmek üzere kullanılır. Ayrıca 2 uzvu uzunluğu eğer sabit uzuv boyutundan kısa ise (a₂ < a₁), 2 uzvu tam bir dönme yapabilecektir. a₁ = a₂ olduğunda ikizkenar kol-kızak mekanizması oluşacaktır.

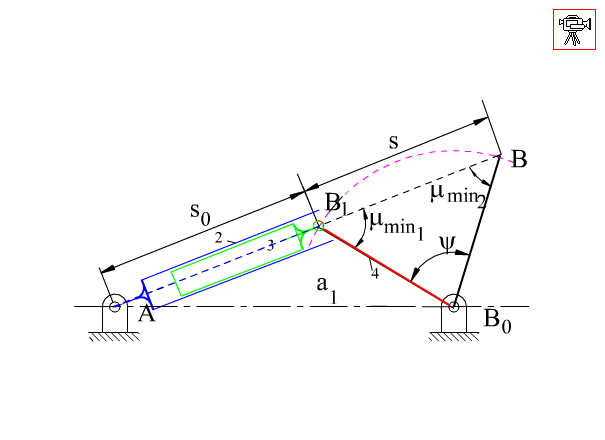
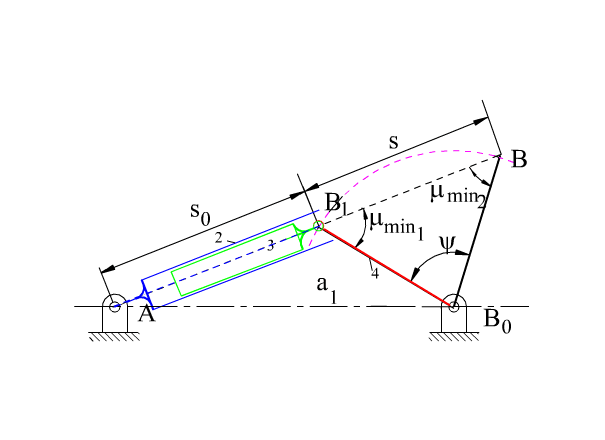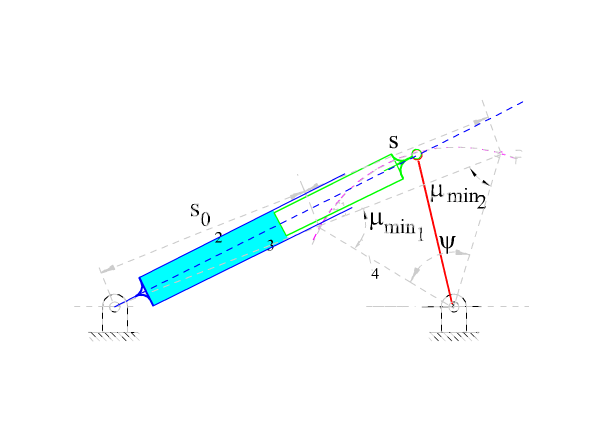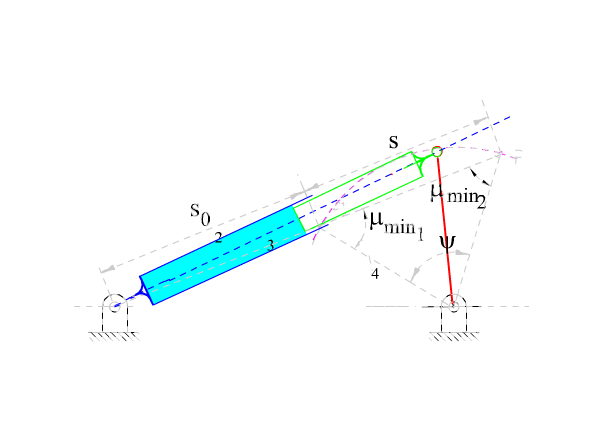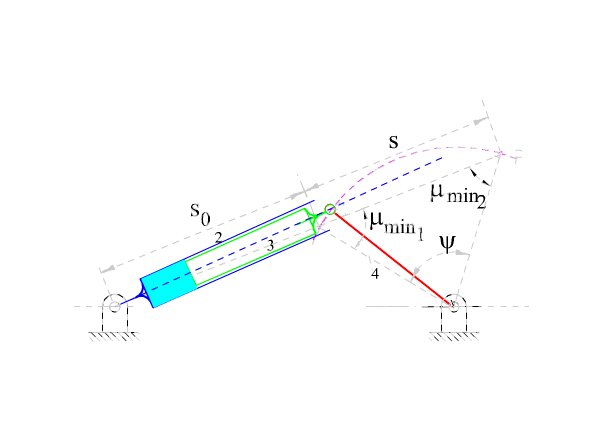
Eksantrik kol-kızak mekanizmasında sınır konumları A₀ merkezli AA₀ yarıçaplı daire ile B₀ merkezli BB₀ (eksantriklik) yarıçaplı dairelere içten ve dıştan teğetler çizerek belirlenir (üstten ikinci şekilde A₀A₁B₁B₀ ve A₀A₂B₂B₀ konumları). Eksantrik kol-kızak mekanizması içinde (1) denklemi, yani ψ + ϕ = 180° bağıntısı aynen geçerli olacaktır. 2 uzvunun tam bir dönme yapabilmesi için ise

a2 + c < a1

(2)

eşitsizliğinin sağlanması gerekir.

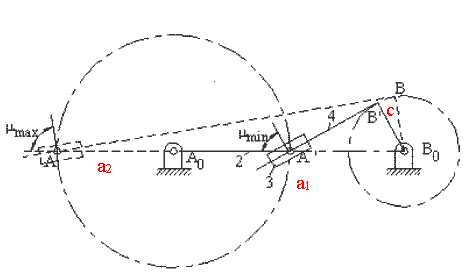
Şu ana kadar açıklanmış olanlar kol-kızak mekanizmasının her iki tipi içinde geçerlidir. Birinci yapıda olan (üstteki şekil) kol-kızak mekanizmaları için ise bağlama açısının tanımlanabildiği ve bağlama açısının en büyük veya en küçük değeri krank ile sabit uzuvların aynı doğrultuda olduğu konumlarda gerçekleştiği gösterilmiştir. Bağlama açısının en büyük ve en küçük değeri bu konumlarda:

\displaystyle \cos {{\text{μ}}_{\begin{smallmatrix} \text{min} \\ \text{max} \end{smallmatrix}}}=\frac{\text{c}}{{{{\text{a}}_{1}}\pm {{\text{a}}_{2}}}}

(3)

Dikkat edilir ise santrik tipte kol-kızak mekanizması için bağlama açısı daima en iyi değer olan 90° değerindedir. Bu nedenle santrik tip kol-kızak mekanizmaları tercih edilir. Ancak daha küçük mekanizma boyutu ile aynı salınım açısı ve karşı gelen kol dönme açısı istenilir ise, eksantrik bir kol-kızak mekanizmasının kullanımı düşünülebilir. En üstteki şekilde gösterilen geometri kullanılarak uzuv boyutları ve salınım açısı arasında mevcut ilişki

\displaystyle \frac{\text{c}}{{{{\text{a}}_{1}}}}=\frac{1}{{\tan \left( {\text{ψ}/2} \right)}}\sqrt{{{{{\sin }}^{2}}\frac{\text{ψ}}{2}-{{{\left( {\frac{{{{\text{a}}_{2}}}}{{{{\text{a}}_{1}}}}} \right)}}^{2}}}}

(4)

veya

\displaystyle \tan \frac{\text{ψ}}{2}=\frac{{\sqrt{{{{\text{a}}_{1}}^{2}-{{{\left( {{{\text{a}}_{2}}-\text{c}} \right)}}^{2}}}}-\sqrt{{{{\text{a}}_{1}}^{2}-{{{\left( {{{\text{a}}_{2}}+\text{c}} \right)}}^{2}}}}}}{{2\text{c}}}

(5)

yazılabilir (eksantriklik sıfır ise c = 0 olacağından, sin(ψ/2) = a₂/a₁ dir).

Görüldüğü gibi bir kol-sarkaç mekanizmasına göre, kol-kızak mekanizmasının tasarımı daha az parametre içerdiğinden dolayı daha kolaydır.

Örnek:

60° salınım açısı olan bir kol-kızak mekanizmasını tasarlıyalım. ψ = 60° olduğundan ϕ = 180° − ψ = 120° olacaktır.ve zaman oranı 240°/120° = 2 dir.

Santrik bir kol-kızak düşünüldüğünde a₂/a₁ = sin(30°) = 0.5 olur. Eksantriklik c/a₁= 0.3 olduğunda ise, denklem (4) ten a₂/a₁ = 0.469 , μ_max = 101.78° ve μ_min = 55.60° olacaktır.

Birinci yapıda kol-kızak mekanizmaları genellikle tam bir dönmeyi belirli bir salınıma dönüştürmek için kullanılırken, ikinci yapıda kol-kızak mekanizmaları genellikle hidrolik tahrik ile bir salınım elde etmek için kullanılır. Bu mekanizmalarda 2 ve 3 uzuvları piston ve silindir olarak tasarlanır ve aralarındaki kayar mafsal silindir içine hava veya sıvı pompalanarak tahrik edilir. Her türlü inşaat makinalalarında, vinçlerde, damperli kamyonlarda ve birçok uygulamada bu mekanizma kullanılmaktadır. Bu uygulamalarda genellikle eksantriklik yoktur. 5. kısımda görüleceği gibi, eksantriklik piston silindir gurubunda istenilmeyen kuvvetlere neden olacaktır. En fazla kullanıldığı durum aşağıda görülmektedir.

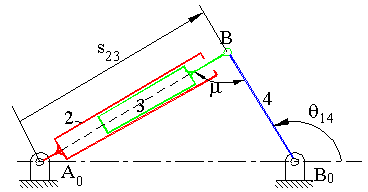
Hidrolik piston ile dönme hareketi elde etmek için kullanılan santrik kol-kızak

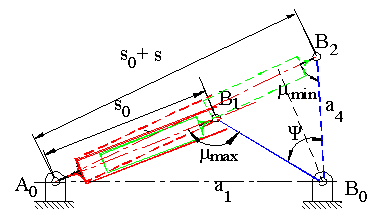
Verilen bir s strokuna karşı gelen kol salınımı (genel)

Verilen bir stroka (s) göre B₀B çıkış uzvu belirli bir miktar (ψ) salınacaktır. Mekanizmanın istenilen kinematik özelliklerle birlikte kuvvet iletiminin de iyi olması istenilir ise, strokun iki uç noktasında oluşan bağlama açısının maksimum ve minimum değerlerinin dik açıdan sapması eşit miktarda olması sağlanmalıdır. Bağlama açısının bu iki sınır konumda dik açıdan eşit sapma göstermesi eğer A₀B₁ ve A₀B₂ doğruları çakışır ise mümkündür. Bu sağlandığında, |B₁B₂| = s dir ve B₁B₀B₂ üçgeni ikizkenar üçgen olup μ_min1 = μ_min2 = 180° − μ_max ve μ_min = 90° − ψ/2 olacaktır. |B₀B| = a₄ kol uzunluğu salınım açısı ve stroka göre

\displaystyle {{\text{a}}_{4}}=\frac{\text{s}}{{2\sin \left( {\text{ψ}/2} \right)}}

dir.

s₀ silindir-piston grubunun minimum boyu (minimum |A₀B| uzunluğu) ise, sabit uzuv boyu |A₀B₀| = a₁

\displaystyle {{\text{a}}_{1}}=\sqrt{{{{{\left( {{{\text{s}}_{0}}+\frac{\text{s}}{2}} \right)}}^{2}}+\frac{{{{\text{s}}^{2}}}}{{4{{{\tan }}^{2}}\left( {\text{ψ}/2} \right)}}}}

(6)

denkleminden bulunabilir. Genellikle s₀ ve s standardtır ve hidrolik piston üreticilerinin kataloglarında bu değerler yer alır (tabi ki istenir ise, maliyeti biraz artsa bile, standard dışı üretilebilir) istenilen salınım açısı ve stroka göre a₁ ve a₄ uzuv boyutları belirlenebilir.