SU2 çözücüsü, yoğunluk-tabanlı (density-based) akışlarda, öncelikle aerodinamik tasarım optimizasyonu ve genel HAD çözümleri için geliştirilmiştir. Bu kapsamda SU2 içerisinde eğim(gradyan)-tabanlı Continous ve Discrete Adjoint yöntemleri bulunmaktadır. [1] Bu yöntemlerin zamana-bağlı çözüm yapabilmesi için gerekli eklemeler daha önce yapılmıştır.
Üzerinde çalışılan fenomen, doğası gereği zamana-bağlı olarak çözülmelidir. Tasarım optimizasyonu işleminde kullanılan Discrete adjoint yöntemi genel olarak zamandan-bağımsız tasarım optimizasyon problemleri için kullanılmaktadır. SU2 çözücüsünde ise bu yöntem zamana-bağlı problemler için de çözülebilmektedir. Genel olarak zamana-bağlı adjoint optimizasyon yöntemi açık-kaynak kodlu ve ticari yazılımlarda bulunmamaktadır. Bu sebepler SU2 çözücüsünün doğru bir tercih olduğunu önermektedir. Ayrıca, SU2 yazılımında zamana-bağlı optimizasyon yönteminin sadece bir kanat profili üzerinde kullanıldığı bilinmektedir. [2]
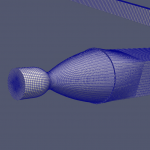
Tasarım optimizasyonu işlemine başlarken ilk olarak geometride değişiklik yapılması planlanan alan ve bu alanda geometri/mesh deformasyonu yapacak yöntem doğru seçilmelidir. SU2 içerisinde Free-Form Deformation (FFD) kutusu denilen bir yöntem ile deformasyon yapılacak katı yüzey bir kutu içine alınır. Bu kutu yüzeyinde bazı kontrol noktaları tanımlanmaktadır. Bu kontrol noktaları daha sonra tasarım değişkenleri olarak da tanımlanmaktadır ve bu noktalar hareket ederek katı yüzeyin, aynı zamanda çözüm ağının, şeklini kontrol etmektedir. Oluşturulan FFD kutu geometrisi görsel 1’de görülebilir.

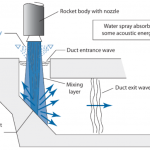
FFD kutusu oluşturulduktan sonra tasarım optimizasyonu için gerekli parametreler SU2 konfigürasyon dosyasında tanımlanmaya başlanabilir. Öncelikle adjoint denklemleri zamana-bağlı çözüleceği için adjoint çözümü zaman-iterasyon adımı sayısı ve hedef fonksiyonu (objective function) belirlenmiştir. Bu tanımlamalardan sonra hedef fonksiyonun ne olacağı ve nerede hesaplanacağı tanımlanmalıdır. Hedef fonksiyonu olarak roket geometrisi üzerinde, görsel 2’te gösterilen yüzeyde, basınç değerlerinin ortalaması alınmıştır.

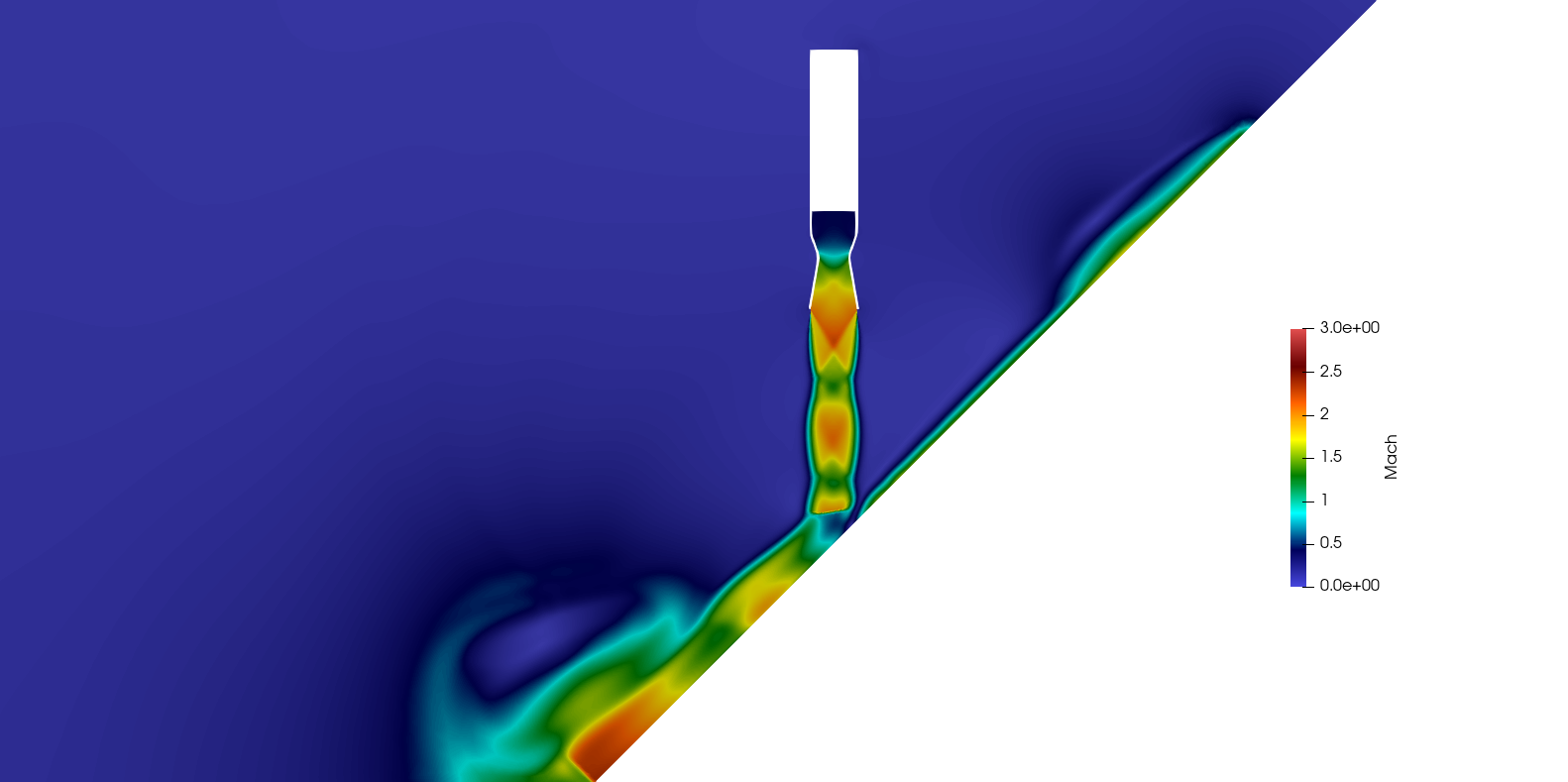
Adjoint yöntemi ile zamana-bağlı tasarım analizi yapmak hem çok fazla CPU zamanı hem de çok fazla depolama alanı gerektirmektedir. Bu sebeple düşük zaman-adımlı sonuçlar almak uzun sürmektedir. Adjoint yönteminde hassaslık (sensitivity) hesaplamaları, HAD ile elde edilen direkt çözümde bulunan veriler kullanılarak geriye doğru iterasyonlar halinde yapılmaktadır. Görsel 2’te görülen sarı renkli roket duvar üzerindeki basıncı minimuma indirmek için hedef fonksiyon ağırlığı -1 olarak tanımlanmıştır. Herhangi bir sınır fonksiyonu (constraint function) tanımlanmamıştır. Tasarım optimizasyon sonucu olarak alınan çıktı aşağıdaki şekildedir.


KAYNAKLAR
[1] Palacios, F., Colonno, M. R., Aranake, A. C., Campos, A., Copeland, S. R., Economon, T. D., Lonkar, A. K., Lukaczyk, T. W., Taylor, T. W. R., and Alonso, J. J., “Stanford University Unstructured (SU2): An Open-Source Integrated Computational Environment for Multi-Physics Simulation and Design,” 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Grapevine, TX, Jan. 7–10, 2013. AIAA 2013-0287.https://doi.org/10.2514/6.2013-0287
[2] Schotthöfer, S., Zhou, B. Y., Albring, T., and Gauger, N. R., “Regularization for Adjoint-Based Unsteady Aerodynamic Optimization Using Windowing Techniques,” AIAA Journal, Vol. 59, No. 7, 2021, pp. 2517–2531. https://doi.org/10.2514/1.J059377